Evanyou Blog 彩带

　题目传送门

Supermarket

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 15192		Accepted: 6855

Description

A supermarket has a set Prod of products on sale. It earns a profit px for each product x∈Prod sold by a deadline dx that is measured as an integral number of time units starting from the moment the sale begins. Each product takes precisely one unit of time for being sold. A selling schedule is an ordered subset of products Sell ≤ Prod such that the selling of each product x∈Sell, according to the ordering of Sell, completes before the deadline dx or just when dx expires. The profit of the selling schedule is Profit(Sell)=Σ_x∈Sellpx. An optimal selling schedule is a schedule with a maximum profit. 
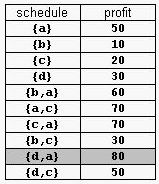
For example, consider the products Prod={a,b,c,d} with (pa,da)=(50,2), (pb,db)=(10,1), (pc,dc)=(20,2), and (pd,dd)=(30,1). The possible selling schedules are listed in table 1. For instance, the schedule Sell={d,a} shows that the selling of product d starts at time 0 and ends at time 1, while the selling of product a starts at time 1 and ends at time 2. Each of these products is sold by its deadline. Sell is the optimal schedule and its profit is 80. 

Write a program that reads sets of products from an input text file and computes the profit of an optimal selling schedule for each set of products. 

Input

A set of products starts with an integer 0 <= n <= 10000, which is the number of products in the set, and continues with n pairs pi di of integers, 1 <= pi <= 10000 and 1 <= di <= 10000, that designate the profit and the selling deadline of the i-th product. White spaces can occur freely in input. Input data terminate with an end of file and are guaranteed correct.

Output

For each set of products, the program prints on the standard output the profit of an optimal selling schedule for the set. Each result is printed from the beginning of a separate line.

Sample Input

4  50 2  10 1   20 2   30 1

7  20 1   2 1   10 3  100 2   8 2
   5 20  50 10

Sample Output

80
185

Hint

The sample input contains two product sets. The first set encodes the products from table 1. The second set is for 7 products. The profit of an optimal schedule for these products is 185.

---

　　传送门（用并查集的解法）

　　分析：又是这道题，不过发现这题还可以用堆来做，于是用堆来重新做一次。也用到了贪心的思想。先将所有商品按过期时间从小到大排序，然后建立一个商品价值的小根堆，依次遍历每个商品，如果发现当前堆的size小于过期日期，则说明现在卖出的商品个数小于其过期日期，就可以直接将该商品的价值丢进堆中;如果发现当前堆的size等于过期日期，则说明直到该商品的过期日期为止每一天都已经有商品卖出了，则比较当前商品价值与堆顶元素大小，如果大于，就将堆顶删除，再将该商品丢进堆中。最后堆中剩下的元素就是我们要卖出的元素，求和输出即可。

　　Code：

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<iomanip>
#include<iostream>
#include<algorithm>
#define Fi(i,a,b) for(int i=a;i<=b;i++)
using namespace std;
const int N=1e4+7;
int n,heap[N],size,ans;
struct Node{int d,v;}a[N];
bool cmp(Node x,Node y)
{return x.d<y.d;}
inline void insert(int x)
{
  heap[++size]=x;int ka=size;
  while(ka>1){
    if(heap[ka]<heap[ka/2])
      swap(heap[ka/2],heap[ka]),ka/=2;
    else break;}
}
inline void delet()
{
  heap[1]=heap[size--];
  int ka=1,s=2;
  while(s<=size){
    if(s<size&&heap[s+1]<heap[s])s++;
    if(heap[s]<heap[ka]){
      swap(heap[ka],heap[s]);ka=s;s=ka*2;}
    else break;}
}
int main()
{
  ios::sync_with_stdio(false);
  while(cin>>n){Fi(i,1,n)cin>>a[i].v>>a[i].d;
    sort(a+1,a+n+1,cmp);ans=0;
    Fi(i,1,n)if(size<a[i].d)insert(a[i].v);
    else if(size==a[i].d)if(a[i].v>heap[1])delet(),insert(a[i].v);
    while(size>0){ans+=heap[1];delet();}cout<<ans<<"
";}
  return 0;
}