一、 问题 现在有一正整数N,要把它分为若干正整数之和,问有多少种本质不同的分法?
(1)其中最大数不超过m, 有多少种分法?
(2)分割后的正整数的数目不超过m个, 有多少种分法?
(3)分成最大数不超过m, 且每一个正整数都是正奇数, 有多少种分法?
(4)分成最大数不超过m, 且每一个正整数都不同,有多少种分法?
(5)分成恰好k个正整数,有多少种分法?
二、分析
(1)最大数不超过 m
(a)设dp[i][j]表示把数字 i 分成最大数不超过 j 的若干正整数之和所得的方法数
(b)有如下递推公式 ,核心是最大数m到底选还是不选
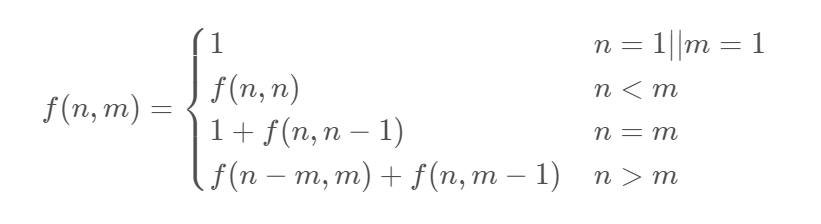
(2)分割数不超过m个
(a)设dp[i][j] 表示把数字 i 分成分割数不超过 j 的若干正整数之和所得的方法数
(b)递推公式核心:
- 到底分不分成 j 个
- 如果分成j个,则预先给每一份分 一个1,那么还剩下n-m,这n-m仍然继续分割成最多j个数;
- 如果不分成j个,那就转移到了把 i 最多分成 j-1 个数的状态
- 递推公式:
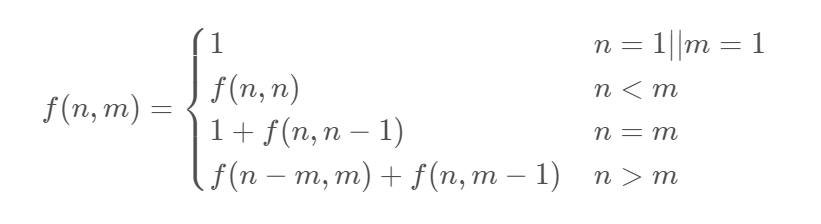
- 发现竟然和(1)完全一样!其实(1)(2)问题是完全等价的
- 从递推公式上来看,等价
- 从图形来看等价:

(3)分成最大数不超过m, 且每一个数都是正奇数
(a)设dp[i][j] 表示把数字 i 分成分割数不超过 j 的若干正奇数之和所得的方法数
(b)递推公式核心: 最大数 j 到底是不是奇数
- 如果是奇数,那么 j 是可以作为 一种分法的元素的 转态转移到到底是分出 j 还是不分出 j
- 如果不是奇数, 那么 j 是不能分出来的,状态转移到了dp[i][j-1]

(4)分成最大数不超过m, 且每一个正整数都不同
(a)设dp[i][j] 表示把数字 i 分成最大数不超过 j 的若干不同正整数之和所得的方法数
(b)递推公式核心:当前最大数选还是不选,如果选,还剩下i-j并且下次的最大数不能再是j而是j-1, 如果不选,状态转移到dp[i][j-1]
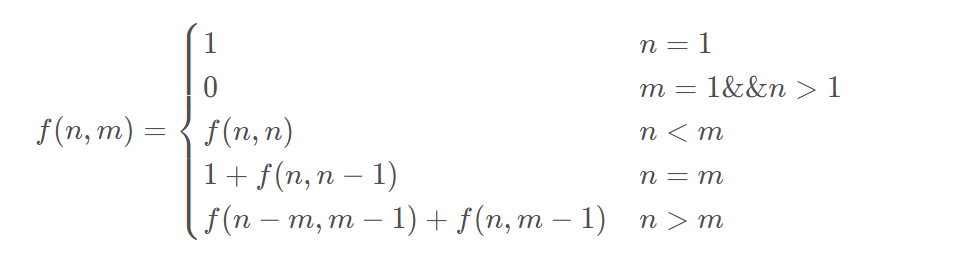
(5)分成恰好k个正整数
(a)设dp[i][j] 表示把数字 i 分成 j 个正整数之和所得的方法数
(b)递推公式核心:
- 这j个数里面含不含有1
- 若不含1,则先为每份预分配一个1,再对i-j进行分割成j份;
- 若含1,则先分出一个1, 然后再对剩下的的i-1分成 j-1份
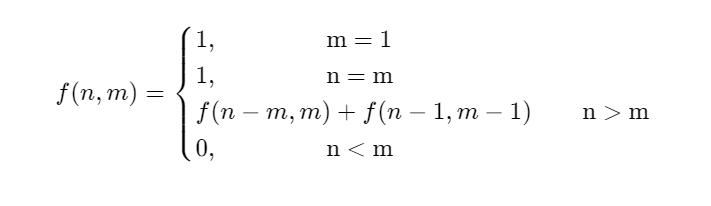
【记忆化搜索代码】

#include<iostream> #include<queue> #include<list> #include<vector> #include<cstring> #include<set> #include<stack> #include<queue> #include<map> #include<set> #include<cmath> #include<algorithm> #include<string> #include<stdio.h> using namespace std; typedef long long ll; const double eps=1e-8; const double PI = acos(-1.0); const int inf = 0x3f3f3f3f; const ll INF = 0x7fffffff; #define MS(x,i) memset(x,i,sizeof(x)) #define rep(i,s,e) for(int i=s; i<=e; i++) #define sc(a) scanf("%d",&a) #define scl(a) scanf("%lld",&a) #define sc2(a,b) scanf("%d %d", &a, &b) #define dubug printf("debug...... "); const int maxn = 1e2+10; int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0 , 0}; /* 1. 把n划分成若干正整数之和 最大数不超过m 方法数 2. 把n划分成不超过m个正整数之和 方法数 1.2 等价 */ ll dp1[maxn][maxn]; ll dp2[maxn][maxn]; ll dp3[maxn][maxn]; ll dp4[maxn][maxn]; //把n划分成不超过m的若干正整数之和 把n划分成不超过m个正整数之和 方法数 ll DP1(int n, int m){ if(dp1[n][m] != -1){ return dp1[n][m]; } ll ans = 0; if(m == 1 || n == 1){ return dp1[n][m] = 1; } if(m == n){ return dp1[n][m] = DP1(n , m - 1) + 1; } if(m > n){ return dp1[n][m] = DP1(n,n); } if(m < n){ return dp1[n][m] = DP1(n-m, m) + DP1(n , m-1); } return dp1[n][m] = 0; } //把N分成不超过m的,若干个正奇数的和 的方法数 ll DP2(int n , int m){ if(dp2[n][m] != -1) return dp2[n][m]; if(n == 1 || m == 1){ return dp2[n][m] = 1; } if(n == m){ return dp2[n][m] = DP2(n , m-1) + m%2; } if(n < m){ return dp2[n][m] = DP2(n , n); } if(n > m){ if(m % 2){ return dp2[n][m] = DP2(n-m , m) + DP2(n , m-1); } else{ return dp2[n][m] = DP2(n , m - 1); } } return dp2[n][m] = 0; } //把N划分成不超过m的 不同正整数之和 的方法数 ll DP3(int n, int m){ if(dp3[n][m] != -1){ return dp3[n][m]; } if(n == 1) return dp3[n][m] = 1; if(m == 1 && n > 1){ return dp3[n][m] = 0; } if(m == n){ return dp3[n][m] = DP3(n , m - 1) + 1; } if(m > n){ return dp3[n][m] = DP3(n,n); } if(m < n){ return dp3[n][m] = DP3(n-m, m-1) + DP3(n , m-1); } return dp3[n][m] = 0; } //把n换分成恰好k个正整数之和 ll DP4(int n, int k){ if(dp4[n][k] != -1) return dp4[n][k]; if(n == 1 && k > 1) return dp4[n][k] = 0; if(k == 1) return dp4[n][k] = 1; if(n == k) return dp4[n][k] = 1; if(n < k) return dp4[n][k] = 0; if(n > k) return dp4[n][k] = DP4(n-k , k) + DP4(n-1, k-1); return 0; } int n,m; int k; int main(){ while(sc(n) != EOF){ MS(dp1, -1); MS(dp2 , -1); MS(dp3 , -1); MS(dp4 , -1); sc(k); //printf("%lld ", DP1(n,n)); printf("%lld ", DP4(n,k)); // printf("%lld ", DP1(n,k)); printf("%lld ", DP3(n,n)); printf("%lld ", DP2(n,n)); } return 0; }
【DP代码】

#include<iostream> #include<queue> #include<list> #include<vector> #include<cstring> #include<set> #include<stack> #include<queue> #include<map> #include<set> #include<cmath> #include<algorithm> #include<string> #include<stdio.h> using namespace std; typedef long long ll; const double eps=1e-8; const double PI = acos(-1.0); const int inf = 0x3f3f3f3f; const ll INF = 0x7fffffff; #define MS(x,i) memset(x,i,sizeof(x)) #define rep(i,s,e) for(int i=s; i<=e; i++) #define sc(a) scanf("%d",&a) #define scl(a) scanf("%lld",&a) #define sc2(a,b) scanf("%d %d", &a, &b) #define dubug printf("debug...... "); const int maxn = 1e2+10; int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0 , 0}; int n; int k; ll dp1[maxn][maxn];//把n划分成若干正整数之和且最大数不超过m 方法数 或者 把n划分成不超过m个正整数之和 方法数 ll dp2[maxn][maxn];//把N分成不超过m的,若干个【正奇数】的和 的方法数 ll dp3[maxn][maxn];//把N划分成不超过m的 【不同】正整数之和的方法数 ll dp4[maxn][maxn];//把n换分成【恰好k个】正整数之和 //把n划分成若干正整数之和且最大数【不超过m】 方法数 或者 把n划分成不超过【m个】正整数之和 方法数 void DP1(){ MS(dp1, 0); rep(i,1,n){ rep(j,1,n){ if(i == 1 || j == 1 ){ dp1[i][j] = 1; continue; } if(j < i) dp1[i][j] = dp1[i-j][j] + dp1[i][j-1]; else if(j > i) dp1[i][j] = dp1[i][i]; else dp1[i][j] = dp1[i][j-1] + 1; } } } //把N分成不超过m的,若干个【正奇数】的和 的方法数 void DP2(){ MS(dp2, 0); rep(i,1,n){ rep(j,1,n){ if(i == 1 || j == 1){ dp2[i][j] = 1; continue; } if(j < i){ if(j % 2) dp2[i][j] = dp2[i-j][j] + dp2[i][j-1]; else{ dp2[i][j] = dp2[i][j-1]; } } else if(j == i){ dp2[i][j] = j%2 + dp2[i][j-1]; } else dp2[i][j] = dp2[i][i]; } } } //把N划分成不超过m的 【不同】正整数之和的方法数 void DP3(){ MS(dp3, 0); rep(i,1,n){ rep(j,1,n){ if(i == 1 ){ dp3[i][j] = 1; continue; } if(j == 1 && i > 1){ dp3[i][j] = 0; continue; } if(i < j) dp3[i][j] = dp3[i][i]; if(i == j ){ dp3[i][j] = 1 + dp3[i][j-1]; } if(i > j){ dp3[i][j] = dp3[i-j][j-1] + dp3[i][j-1]; } } } // cout<<dp3[5][5]<<endl; } //把n换分成【恰好k个】正整数之和 void DP4(){ MS(dp4 , 0); rep(i, 1, n) { rep(j , 1, n){ // if(i == 1 && j > 1) { // dp4[i][j] = 0; // continue; // } if(j == 1) { dp4[i][j] = 1; continue; } if(i == j) dp4[i][j] = 1; if(i > j) dp4[i][j] = dp4[i-j][j] + dp4[i-1][j-1]; if(i < j) dp4[i][j] = 0; } } } int main(){ while(sc(n) != EOF){ sc(k); DP1(); DP2(); DP3(); DP4(); cout<<dp4[n][k]<<endl; cout<<dp3[n][n]<<endl; cout<<dp2[n][n]<<endl; } return 0; }
- (1)(2)等价旋转图来自博客:https://blog.csdn.net/starter_____/article/details/83003200
