核函数（kernel function）

在接触反演、算法等方面的知识后，经常听到“核”这个字，它不像对原始变量的线性变换，也不像类似于机器学习中激活函数那样的非线性变换，对原始数据进行变换，就可以将复杂的问题简单化。接下来，就让我们了解了解“核”这个东西。

参考链接：

1. 通俗理解核方法（kernel function）

2. 核技巧（kernel trick）

注，kernel function 与kernel function指的是同一个东西，可以这样理解：核方法只是一种处理问题的技巧，低维空间线性不可分可以在高维空间线性可分，但是高维空间的计算复杂度又很大，那么我们就把高维空间的计算通过低维空间的计算外加一些线性变换来完成。

还有，都说核方法与映射无关，怎么理解呢？核方法是一种技巧，不管怎么映射，我们都是用低维空间的计算来解决高维空间计算复杂的问题。

1. 问题描述

给定两个向量(x_i)和(x_j)，我们的目标是要计算他们的内积(I) = <(x_i), (x_j)>。现在假设我们通过某种非线性变换：(Phi : x ightarrow phi(x))把他们映射到某一个高维空间中去，那么映射后的向量就变成：(phi(x_i))和(phi(x_j))，映射后的内积就变成：(I’) = <(phi(x_j)),(phi(x_j))>。

现在该如何计算映射后的内积呢？

传统方法是先计算映射后的向量(phi(x_i))和(phi(x_j))，然后再计算它俩的内积。但是这样做计算很复杂，因为映射到高维空间后的数据维度很高。比如，假设(x_i)和(x_j)在映射之后都是一个( (1 imes 10000))维的向量，那么他们的内积计算就需要做10000次加法操作和10000次乘法操作，显然复杂度很高。

于是，数学家们就想出一个办法：能不能在原始空间找到一个函数(K(x_i,x_j))使得(K(x_i,x_j) = <phi(x_j),phi(x_j)>)呢？ 如果这个函数存在，那么我们只需要在低维空间里计算函数(K(x_i,x_j))的值即可，而不需要先把数据映射到高维空间，再通过复杂的计算求解映射后的内积了。庆幸的是，这样的函数是存在的。这样一来计算的复杂度就大大降低了，这种简化计算的方法被称为核技巧（The Kernel Trick），而函数(K)就是核函数（Kernel Function）。

2. 与SVM的关系

之前的一篇介绍支持向量机的文章里我们说过：支持向量机为了解决数据在低维度不容易线性分割的情况下，会通过某非线性变换 (phi(x))，将输入空间映射到高维特征空间。于是，就得到如下求解公式：

[egin{aligned} & sum_{i=1}^{N}sum_{j=1}^{N}alpha_ialpha_jy_iy_jphi(x_i)^{T}phi(x_j)-sum_{i=1}^{N}alpha_i\ ext{s.t.} & space 0leqalpha_1leq C , space sum_{i=1}^{N} y_{i}alpha _{i}=0end{aligned} ]

观察上面的公式你会发现里面有一个内积运算

[phi left ( x_{i} ight )^{T}phi left ( x_{j} ight ) ]

于是，为了降低计算复杂度，解决映射后可能产生的维度爆炸问题，我们在求解的时候引入了核技巧。核技巧并不仅仅应用在SVM中，在其他需要处理高维映射计算的问题中也有很多应用。

3. 常用的核函数

主要有以下几种：

• 线性核，其实就是没有映射

  [kappa left ( x_{1},x_{2} ight ) = left langle x{1},x{2} ight angle ]

• 高斯核函数，使用最为广泛，它能够把原始特征映射到无穷维。

  [kappa left ( x_{1},x_{2} ight ) = exp left ( -frac{left | x_{1}-x_{2} ight |^{2}}{2sigma ^{2}} ight ) ]

• 多项式核函数，它能把数据映射到(C_{n+d}^{n})维。

  [kappa left ( x_{1},x_{2} ight ) = left ( left langle x_{1},x_{2} ight angle +R ight )^{d} ]

由此可见：选择什么样的核函数将会决定你把数据映射到什么样的维度。

4. 核函数的满足条件

Mercer 定理：任何半正定的函数都可以作为核函数。所谓半正定的函数(f(x_i,x_j))，是指拥有训练数据集合(x_1,x_2,…x_n)，我们定义一个矩阵的元素(a_{ij} = f(x_i,x_j))，这个矩阵是(n imes n)的，如果这个矩阵是半正定的，那么(f(x_i,x_j))就称为半正定的函数。

这个mercer定理不是核函数必要条件，只是一个充分条件，即还有不满足mercer定理的函数也可以是核函数。

5. 核函数的计算

在上面了解了核函数是什么后，我们已经知道了核函数与内积之间的关系，接下来，从理论上看一看。

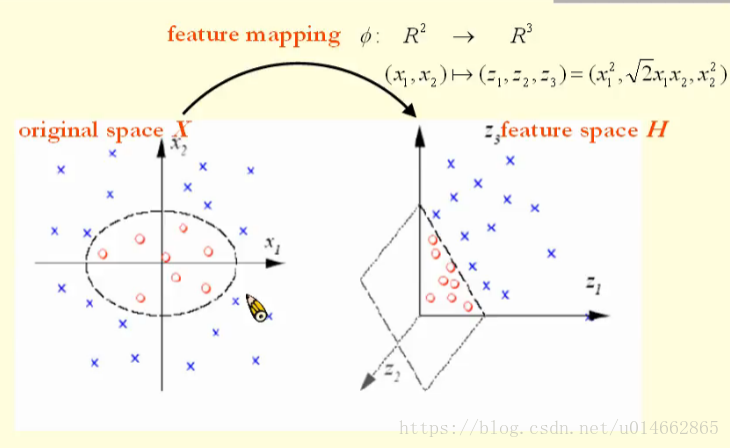
从图中可以看出，在original space的数据，其带有两种标签，如果要将这两种数据分开，必须通过一个椭圆来分开，也就是说，它不是线性可分的；

那么，有什么办法呢？

如图所示，对original space的数据进行feature mapping，从而把数据从((x_1,x_2))的二维空间映射到((z_1,z_2,z_3))的三维空间中，很明显，在三维空间的数据能够很容易的通过一个超平面将数据进行分类，也就是说，该数据在更加高维的空间变得线性可分了。

但是，这和内积有啥关系呢？

比如，在((x_1,x_2))的二维空间中，

[egin{aligned}x &=(x_1,x_2) \x'&=(x_1',x_2')end{aligned} ]

也就是说，(x)和(x')表示((x_1,x_2))二维空间中的两个点，(phi(cdot))表示从二维空间到三维空间的映射函数，则(x)和(x')对应的三维空间的点分别为(phi(x))和(phi(x'))。

接下来，我们从计算上看看线性可分与线性不可分的区别？

如上图所示，对于可以线性可分的数据，数据的类别之间可以由一个超平面分隔开，从图中可以看出来，超平面有很多个满足将数据的两种类别分隔开的条件，因此，我们可以取两种类别数据的质点，对应图中的(c_-)和(c_+)，这两点连线(overrightarrow{c_-c_+})（对应图中红线），那么最优的超平面就可以取为以(overrightarrow{c_-c_+})为法向量、过(overrightarrow{c_-c_+})的中点(c=frac{1}{2}(c_-+c_+))的那个平面，即(H(x)=overrightarrow{c_-c_+}(phi(x)-c)=w^T(phi(x)-c))。

但是，对于线性不可分的情况，就没有这么好了，我们可以通过机器学习中的激活函数（非线性表示）来学习二分类的边界，学个椭圆不是问题，但是，如果要通过线性可分这样的内积方式获得，显然是不现实的。

内积的具体应用如何？

(phi(x))和(phi(x'))是低维空间的点(x)和(x')映射到高维空间的表示，两点之间的距离为

[egin{aligned}||phi(x)-phi(x')||^2 &= (phi(x)-phi(x'))^T(phi(x)-phi(x'))\&= phi(x)^Tphi(x)-phi(x)^Tphi(x')-phi(x')^Tphi(x)+phi(x')^Tphi(x)\&= <phi(x),phi(x)>-<phi(x),phi(x')>-<phi(x'),phi(x)>+<phi(x'),phi(x')>\&= <phi(x),phi(x)>-2<phi(x),phi(x')>+<phi(x'),phi(x')>end{aligned} ]

对于其中的(<phi(x),phi(x')>)项，可做如下方式展开：

[egin{aligned}<phi(x),phi(x')> &=||phi(x)||cdot||phi(x')||cos heta\& Downarrow \cos heta &= frac{<phi(x),phi(x')>}{||phi(x)||cdot||phi(x')||}\ &= frac{<phi(x),phi(x')>}{sqrt{<phi(x),phi(x)>}sqrt{<phi(x'),phi(x')>}}end{aligned} ]

这样，我们就可以得到高维空间两个点的距离、夹角信息，从而可以计算出超平面。

内积在核函数中的应用？

根据上面的分析可知，理论超平面为(H(x)=overrightarrow{c_-c_+}(phi(x)-c)=w^T(phi(x)-c))

转换成内积形式：

[egin{aligned}<phi(x)-c,w> &= w^T(phi(x)-c)\&= w^Tphi(x) - w^Tc\&= overrightarrow{c_-c_+}^Tphi(x)-overrightarrow{c_-c_+}^Tc\&= (c_+-c_-)^Tphi(x) - frac{1}{2}(c_+-c_-)^T(c_++c_-)\&= [frac{1}{m_+}sum_{(i|y_i=1)}phi(x_i)-frac{1}{m_-}sum_{(i|y_i=-1)}phi(x_i)]^Tphi(x)-(frac{1}{2}c_+^Tc_+-c_+^Tc_-+frac{1}{2}c_-^Tc_-)\&= [frac{1}{m_+}sum_{(i|y_i=1)}phi(x_i)^Tphi(x)-frac{1}{m_-}sum_{(i|y_i=-1)}phi(x_i)^Tphi(x)]-b\&= [frac{1}{m_+}sum_{(i|y_i=1)}kappa(x,x_i)-frac{1}{m_-}sum_{(i|y_i=-1)}kappa(x,x_i)]-bend{aligned} ]

其中的(kappa(x,x_i))表示核函数，即高维空间中两个点的内积。

所谓核函数，就是在原空间上两个点内积的一个函数得到的。

举例如下，

((x_1,x_2) ightarrow (z_1,z_2,z_3)=(x_1^2,sqrt{2}{x_1x_2},x_2^2）)

[egin{aligned}<phi(x_1,x_2),phi(x_1',x_2')> &= <(z_1,z_2,z_3),(z_1',z_2',z_3')>\&= <(x_1^2,sqrt{2}x_1x_2,x_2^2),(x_1'^2,sqrt{2}x_1'x_2,x_2^2)>\&= x_1^2x_1'^2+2x_1x_2x_1'^2x_2'2+x_2^2x_2'^2\&= (x_1x_1'^2+x_2x_2'^2)^2\&= (<x,x’>)^2\&= kappa(x,x')end{aligned} ]

从上述公式可以看出，核函数是一个用原有特征空间上点内积的方式通过运算转换成高维空间点内积，而不必完全有高维空间上的点进行计算，从而到达降低运算复杂度的作用。

6. 常用核函数的理解

以高斯核函数为例，

[kappa left ( x_{1},x_{2} ight ) = exp left ( -frac{left | x_{1}-x_{2} ight |^{2}}{2sigma ^{2}} ight ) ]

我们假设(sigma = 1)，则

[egin{aligned}kappa left ( x_{1},x_{2} ight ) & = exp left ( -frac{left | x_{1}-x_{2} ight |^{2}}{2sigma ^{2}} ight )\& = exp(-(x_1-x_2)^2)\& = exp(-x_1^2)exp(-x_2^2)exp(2x_1x_2)\& underrightarrow{ ext{Taylor}}\& = exp(-x_1^2)exp(-x_2^2)(sum_{i=0}^{infty}frac{(2x_1x_2)^i}{i!})\& = sum_{i=0}^{infty}(exp(-x_1^2)exp(-x_2^2)sqrt{frac{2^i}{i!}}sqrt{frac{2^i}{i!}}x_1^i x_2^i)\& = sum_{i=0}^{infty}([exp(-x_1^2)sqrt{frac{2^i}{i!}}x_1^i][exp(-x_2^2)sqrt{frac{2^i}{i!}} x_2^i])\& = phi(x_1)^Tphi(x_2)end{aligned} ]

这不，已经有了定义的那种形式，对于(phi(x))，由于

[phi(x)=exp(-x^2)cdot(1,sqrt{frac{2^1}{1!}}x,sqrt{frac{2^2}{2!}}x^2,cdots) ]

所以，可以映射到任何一个维度上。