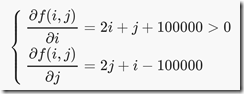POJ 3579 3685（二分-查找第k大的值）

POJ 3579

题意

双重二分搜索：对列数X计算∣X_i – X_j∣组成新数列的中位数

思路

对X排序后，与X_i的差大于mid（也就是某个数大于X_i + mid）的那些数的个数如果小于N / 2的话，说明mid太大了。以此为条件进行第一重二分搜索，第二重二分搜索是对X的搜索，直接用lower_bound实现。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;

int N;
int CN2 = 0;
int X[100005];
bool C(int x) { // 验证x作为中位数 x = X[j] - X[i] 是否太小
	int cnt = 0;
	for (int i = 0; i<N; ++i) {
		cnt += N - (lower_bound(X + i, X + N, X[i] + x) - X); // 统计差值>=x的个数
	}
	return cnt > CN2 >> 1;
}
void solve() {
	sort(X, X + N);
	CN2 = N*(N - 1) >> 1;
	int lb = 0, ub = 1000000001;
	while (ub - lb > 1) {
		int mid = (ub + lb) >> 1;
		if (C(mid)) lb = mid; // 中位数过小，半闭半开区间[lb, ub)
		else ub = mid;
	}
	printf("%d
", lb);
}
int main()
{
	while (scanf("%d", &N) == 1) {
		for (int i = 0; i < N; ++i) scanf("%d", X + i);
		solve();
	}
	return 0;
}

POJ 3685

题意：边为n的方阵中，aij=i^2+100000i+j^2-100000j+i*j，求矩阵的第k大数。

思路：需要注意数据规模，特别是1≤M≤N×N，需要64位变量来存

首先来分析下这个函数f(i,j)

可知f(i,j)按行递增（同列），而按列不单调（同行）。

设C(x)表示矩阵中<x的元素有多少个。 所以可以一列一列来求有多少个比x小。然后二分求出正好有M−1个数比x小即可。

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll MAX = 1e15;
ll T;
ll N, M;
ll f(ll i, ll j) {
	return i*i + 100000 * (i - j) + i*j + j*j;
}
bool C(ll x) { // 验证x是否过小。。。。这里写成int x调了好久= =
	ll cnt = 0; // cnt 为<x的个数
	for (int j = 1; j <= N; ++j) {
		int lb = 0, ub = N + 1; // (lb, ub)
		while (ub - lb > 1) {
			int mid = (lb + ub) >> 1;
			if (f(mid, j) < x) lb = mid; // 半闭半开区间[lb, ub)
			else ub = mid;
		}
		cnt += lb;
	}
	return cnt < M;
}
void solve() {
	ll lb = f(0, N), ub = f(N, 0) + 1;
	while (ub - lb > 1) {
		ll mid = (ub + lb) >> 1;
		if (C(mid)) lb = mid; // 半闭半开区间[lb, ub)
		else ub = mid;
	}
	cout << lb << endl;
}
int main() {
	cin >> T;
	while (T--) {
		cin >> N >> M;
		solve();
	}
	return 0;
}