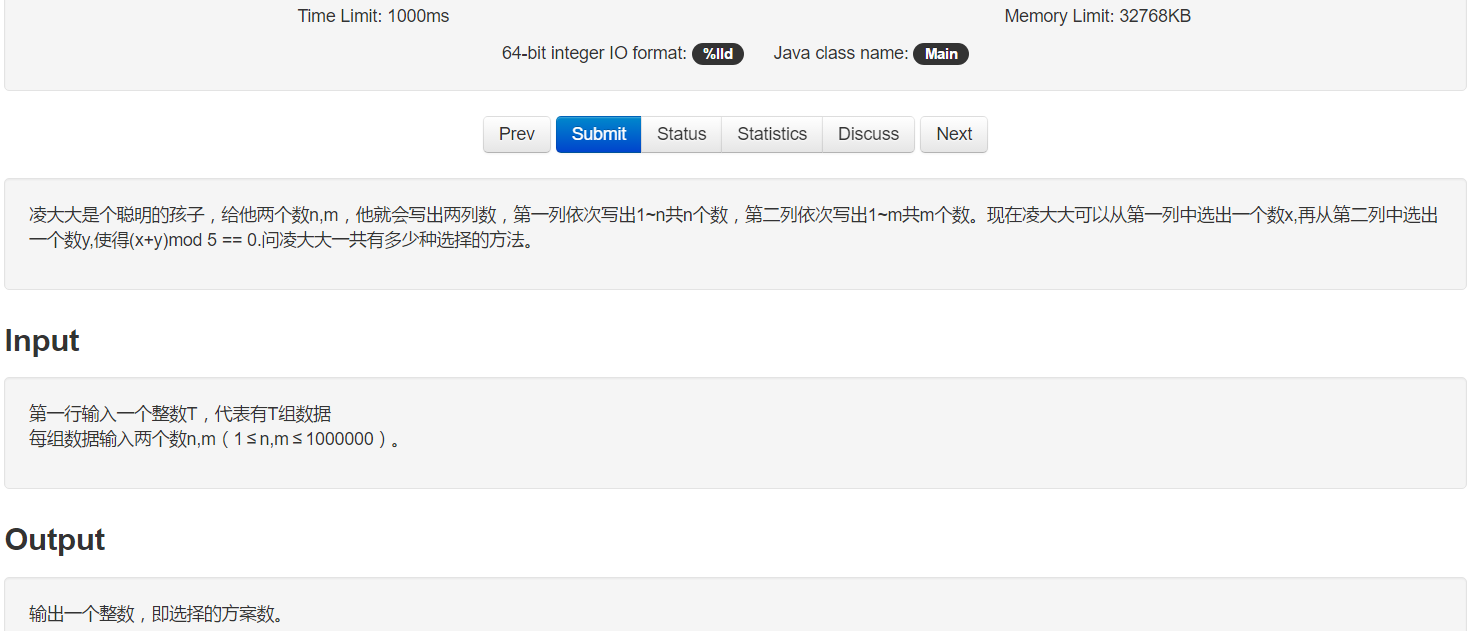
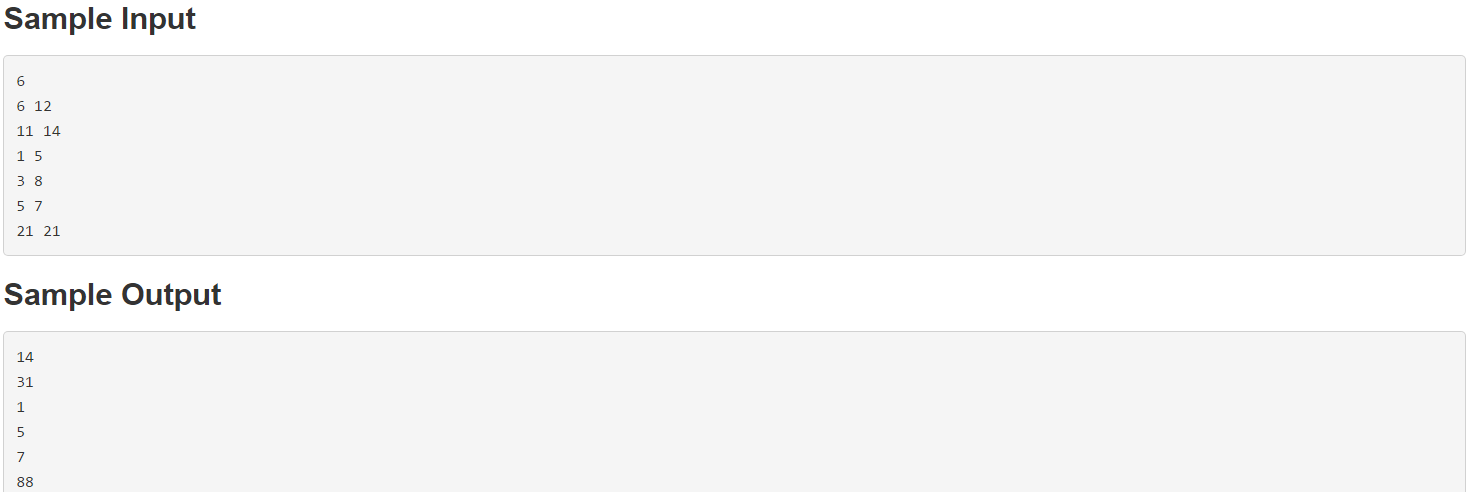
首先,可以自己先一个超时的标程出来:
1 #include<cstdio> 2 typedef long long ll; 3 ll n,m,cnt; 4 int main() 5 { 6 int t; 7 scanf("%d",&t); 8 while(t--) 9 { 10 scanf("%d%d",&n,&m); 11 cnt=0; 12 for(int i=1;i<=n;i++) 13 { 14 for(int j=1;j<=m;j++) 15 { 16 if((i+j)%5==0) cnt++; 17 } 18 } 19 printf("%lld ",cnt); 20 } 21 }
那么考虑如何进行时间优化:

这样一来,原本例如(2 + 3)mod 5 = 0 的情况,我们得到的是 ( i_num = 1 ) * ( j_num = 1 ) = 1,1对( i , j ),
现在就可以使 ( i_num = 2 ) * ( j_num = 3 ) = 6,6对( i , j )
因此可以得到一个优化了时间复杂的算法:
1 #include<cstdio> 2 #include<cstring> 3 typedef long long ll; 4 ll n,m,cnt,i_mod5_equal[5],j_mod5_equal[5]; 5 int main() 6 { 7 int t; 8 scanf("%d",&t); 9 while(t--) 10 { 11 scanf("%lld%lld",&n,&m); 12 13 cnt=0; 14 for(int i=0;i<=4;i++) i_mod5_equal[i]=0; 15 for(int i=1;i<=n;i++) i_mod5_equal[(i%5)]++; 16 17 for(int j=0;j<=4;j++) j_mod5_equal[j]=0; 18 for(int j=1;j<=m;j++) j_mod5_equal[(j%5)]++; 19 20 for(int i=0;i<=4;i++){ 21 for(int j=0;j<=4;j++){ 22 if((i+j)%5==0) cnt+=i_mod5_equal[i]*j_mod5_equal[j]; 23 } 24 } 25 printf("%lld ",cnt); 26 } 27 }
显然,这样一个O(n)的算法,依然比较慢,还可以进一步优化:
1 #include<cstdio> 2 #include<cstring> 3 typedef long long ll; 4 ll n,m,cnt,i_mod5_equal[5],j_mod5_equal[5]; 5 int main() 6 { 7 int t; 8 scanf("%d",&t); 9 while(t--) 10 { 11 scanf("%lld%lld",&n,&m); 12 13 cnt=0; 14 for(int i=0;i<=4;i++) i_mod5_equal[i]=n/5; 15 for(int i=1;i<=n%5;i++) i_mod5_equal[i]++; 16 17 for(int j=0;j<=4;j++) j_mod5_equal[j]=m/5; 18 for(int j=1;j<=m%5;j++) j_mod5_equal[j]++; 19 20 for(int i=0;i<=4;i++){ 21 for(int j=0;j<=4;j++){ 22 if((i+j)%5==0) cnt+=i_mod5_equal[i]*j_mod5_equal[j]; 23 } 24 } 25 printf("%lld ",cnt); 26 } 27 }
这样就得到了一个O(1)的算法。
两次的时间比较很明显:
