HDU 5954

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5954

Problem Description
You have got a cylindrical cup. Its bottom diameter is 2 units and its height is 2 units as well.
The height of liquid level in the cup is d (0 ≤ d ≤ 2). When you incline the cup to the maximal angle such that the liquid inside has not been poured out, what is the area of the surface of the liquid?

Input
The first line is the number of test cases. For each test case, a line contains a float-point number d.

Output
For each test case, output a line containing the area of the surface rounded to 5 decimal places.

Sample Input
4
0
1
2
0.424413182

Sample Output
0.00000
4.44288
3.14159
3.51241

题意：

有一个圆柱形杯子，底部直径为 $2$，高为 $2$，告诉你当杯子水平放置时水面高度为 $d(0 le d le 2)$，

求当在水不倒出来的前提下杯子倾斜角度最大时，水面面积。

题解：

（参考https://blog.csdn.net/danliwoo/article/details/53002695）

当 $d=1$ 时，是临界情况。

当 $d>1$ 时，水面为一个椭圆，设 $ heta$ 为水面与杯底的夹角，则 $S = pi R r = pi cdot frac{1}{cos heta} cdot 1 = frac{pi}{cos heta}$。

当 $d<1$ 时，水面为一个椭圆截取一部分：

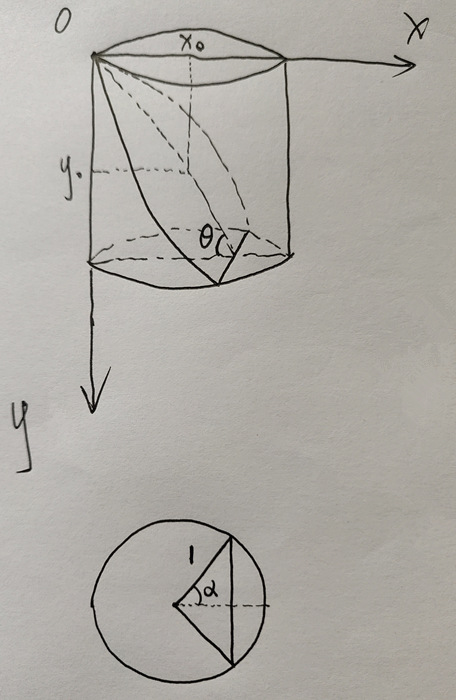若将水此时的形状，按平行于杯底的方向，分割成若干薄面，每个薄面的面积为 $S_0$，则水的体积为

$V = int_{0}^{2}S_0dy$；

不难求得

$y_0 = x_0 tan heta$

$1 + cos alpha = x_0$

$S_0 = pi - alpha + sin alpha cos alpha$

上三式，对于 $0 le alpha le pi$（即 $2 ge x_0 ge 0$）均成立。

则水的体积定积分可变为

$V = int_{0}^{2}(pi - alpha + sin alpha cos alpha)d[(1 + cos alpha) an heta]$

即

$ an heta int_{pi}^{alpha_1}(pi - alpha + sin alpha cos alpha)(- sin alpha)dalpha$

其中 $alpha_1 = arccos(frac{2}{ an heta}-1)$。

对上式积分得

$V = an heta [(pi cos alpha) + (sin alpha - alpha cos alpha) - frac{1}{3} sin^3 alpha]_{pi}^{alpha_1}$

那么，我们可以二分 $ heta$，使得 $V$ 逼近 $pi d$，从而确定 $ heta$，进而用 $S_{斜面} = frac{S_{底面}}{cos heta}$ 求得水面面积。

 

AC代码：

#include<bits/stdc++.h>
using namespace std;
const double pi=acos(-1.0);
const double eps=1e-12;
inline bool equ(double x,double y){return fabs(x-y)<eps;}
inline double a_t(double t) {
    double tmp=2.0/tan(t);
    if(tmp>2) tmp=2.0;
    else if(tmp<0) tmp=0.0;
    return acos(tmp-1.0);
}
inline double I(double a) {
    return pi*cos(a)+sin(a)-a*cos(a)-pow(sin(a),3)/3.0;
}
inline double V(double t) {
    if(equ(t,pi/2.0)) return 0;
    else return tan(t)*(I(a_t(t))-I(pi));
}
int main()
{
    int T;
    double d;
    cin>>T;
    while(T--)
    {
        cin>>d;
        if(equ(d,0))
        {
            printf("%.5f
",0);
            continue;
        }
        if(d>1)
        {
            printf("%.5f
",pi/cos(atan(2-d)));
            continue;
        }

        double l=pi/4.0, r=pi/2.0, t;
        while(r-l>eps)
        {
            t=(l+r)/2;
            if(equ(V(t),pi*d)) break;
            else if(V(t)>pi*d) l=t;
            else r=t;
        }
        double a=a_t(t);
        double S=pi-a+sin(a)*cos(a);
        printf("%.5f
",S/cos(t));
    }
}