转自 https://www.cnblogs.com/maybe2030/p/4715035.html
部分内容来自尚硅谷视频
- 1. 顺序查找
- 2. 二分查找
- 3. 插值查找
- 4. 斐波那契查找
- 5. 树表查找
- 6. 分块查找
- 7. 哈希查找
查找算法
查找定义:根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。
查找算法分类:
1)静态查找和动态查找;
注:静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
2)无序查找和有序查找。
无序查找:被查找数列有序无序均可;
有序查找:被查找数列必须为有序数列。
1. 顺序查找
说明:顺序查找适合于存储结构为顺序存储或链接存储的线性表。
基本思想:顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
复杂度分析:
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
当查找不成功时,需要n+1次比较,时间复杂度为O(n);
所以,顺序查找的时间复杂度为O(n)。
2.二分查找
说明:元素必须是有序的,如果是无序的则要先进行排序操作。
基本思想:也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
复杂度分析:最坏情况下,关键词比较次数为log2(n+1),且期望时间复杂度为O(log2n);
注:折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。
//二分查找(折半查找),版本1 int BinarySearch1(int a[], int value, int n) { int low, high, mid; low = 0; high = n-1; while(low<=high) { mid = (low+high)/2; if(a[mid]==value) return mid; if(a[mid]>value) high = mid-1; if(a[mid]<value) low = mid+1; } return -1; } //二分查找,递归版本 int BinarySearch2(int a[], int value, int low, int high) { int mid = low+(high-low)/2; if(a[mid]==value) return mid; if(a[mid]>value) return BinarySearch2(a, value, low, mid-1); if(a[mid]<value) return BinarySearch2(a, value, mid+1, high); }
3. 插值查找
//插值查找 int InsertionSearch(int a[], int value, int low, int high) { int mid = low+(value-a[low])/(a[high]-a[low])*(high-low); if(a[mid]==value) return mid; if(a[mid]>value) return InsertionSearch(a, value, low, mid-1); if(a[mid]<value) return InsertionSearch(a, value, mid+1, high); }
4. 斐波那契查找
在介绍斐波那契查找算法之前,我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。
黄金比例又称黄金分割,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1:0.618或1.618:1。
0.618被公认为最具有审美意义的比例数字,这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。
大家记不记得斐波那契数列:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….(从第三个数开始,后边每一个数都是前两个数的和)。然后我们会发现,随着斐波那契数列的递增,前后两个数的比值会越来越接近0.618,利用这个特性,我们就可以将黄金比例运用到查找技术中
斐波那契(黄金分割法)原理:
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid不再是中间或插值得到,而是位于黄金分割点附近,即mid=low+F(k-1)-1(F代表斐波那契数列),如下图所示
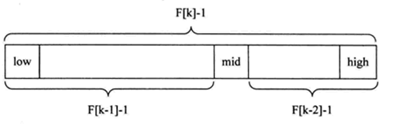
对F(k-1)-1的理解:
由斐波那契数列 F[k]=F[k-1]+F[k-2] 的性质,可以得到 (F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1 。该式说明:只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段,即如上图所示。从而中间位置为mid=low+F(k-1)-1
类似的,每一子段也可以用相同的方式分割
但顺序表长度n不一定刚好等于F[k]-1,所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只要能使得F[k]-1恰好大于或等于n即可,由以下代码得到,顺序表长度增加后,新增的位置(从n+1到F[k]-1位置),都赋为n位置的值即可。
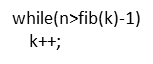
package com.atguigu.search; import java.util.Arrays; public class FibonacciSearch { public static int maxSize = 20; public static void main(String[] args) { int [] arr = {1,8, 10, 89, 1000, 1234}; System.out.println("index=" + fibSearch(arr, 189));// 0 } //因为后面我们mid=low+F(k-1)-1,需要使用到斐波那契数列,因此我们需要先获取到一个斐波那契数列 //非递归方法得到一个斐波那契数列 public static int[] fib() { int[] f = new int[maxSize]; f[0] = 1; f[1] = 1; for (int i = 2; i < maxSize; i++) { f[i] = f[i - 1] + f[i - 2]; } return f; } //编写斐波那契查找算法 //使用非递归的方式编写算法 /** * * @param a 数组 * @param key 我们需要查找的关键码(值) * @return 返回对应的下标,如果没有-1 */ public static int fibSearch(int[] a, int key) { int low = 0; int high = a.length - 1; int k = 0; //表示斐波那契分割数值的下标 int mid = 0; //存放mid值 int f[] = fib(); //获取到斐波那契数列 //获取到斐波那契分割数值的下标 while(high > f[k] - 1) { k++; } //因为 f[k] 值 可能大于 a 的 长度,因此我们需要使用Arrays类,构造一个新的数组,并指向temp[] //不足的部分会使用0填充 int[] temp = Arrays.copyOf(a, f[k]); //实际上需求使用a数组最后的数填充 temp //举例: //temp = {1,8, 10, 89, 1000, 1234, 0, 0} => {1,8, 10, 89, 1000, 1234, 1234, 1234,} for(int i = high + 1; i < temp.length; i++) { temp[i] = a[high]; } // 使用while来循环处理,找到我们的数 key while (low <= high) { // 只要这个条件满足,就可以找 mid = low + f[k - 1] - 1; if(key < temp[mid]) { //我们应该继续向数组的前面查找(左边) high = mid - 1; //为甚是 k-- //说明 //1. 全部元素 = 前面的元素 + 后边元素 //2. f[k] = f[k-1] + f[k-2] //因为 前面有 f[k-1]个元素,所以可以继续拆分 f[k-1] = f[k-2] + f[k-3] //即 在 f[k-1] 的前面继续查找 k-- //即下次循环 mid = f[k-1-1]-1 k--; } else if ( key > temp[mid]) { // 我们应该继续向数组的后面查找(右边) low = mid + 1; //为什么是k -=2 //说明 //1. 全部元素 = 前面的元素 + 后边元素 //2. f[k] = f[k-1] + f[k-2] //3. 因为后面我们有f[k-2] 所以可以继续拆分 f[k-1] = f[k-3] + f[k-4] //4. 即在f[k-2] 的前面进行查找 k -=2 //5. 即下次循环 mid = f[k - 1 - 2] - 1 k -= 2; } else { //找到 //需要确定,返回的是哪个下标 if(mid <= high) { return mid; } else { return high; } } } return -1; } }
5. 树表查找
5.1 最简单的树表查找算法——二叉树查找算法。
基本思想:二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
二叉查找树(BinarySearch Tree,也叫二叉搜索树,或称二叉排序树Binary Sort Tree)或者是一棵空树,或者是具有下列性质的二叉树:
1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2)若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3)任意节点的左、右子树也分别为二叉查找树。