Codeforces Round #407 (Div. 1)

人傻不会B 写了C正解结果因为数组开小最后RE了 疯狂掉分

AC:A Rank:392 Rating: 2191-92->2099

A. Functions again

题目大意：给定一个长度为n的数组，求最大的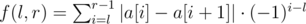，其中1<=l<r<=n。（n<=10^5）

思路：按左端点所在位置的奇偶性分开计算即可。

#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long
char B[1<<26],*S=B,C;int X,F;
inline int read()
{
    for(F=1;(C=*S++)<'0'||C>'9';)if(C=='-')F=-1;
    for(X=C-'0';(C=*S++)>='0'&&C<='9';)X=(X<<3)+(X<<1)+C-'0';
    return X*F;
}
#define MN 200000
int a[MN+5];
ll s[MN+5];
int main()
{
    fread(B,1,1<<26,stdin);
    int n=read(),i,p;long long mx=0,mn;
    for(i=1;i<=n;++i)a[i]=read();
    for(mn=0,i=p=1;i<n;++i,p*=-1)
    {
        s[i]=s[i-1]+abs(a[i+1]-a[i])*p;
        mx=max(mx,s[i]-mn);
        if(~i&1)mn=min(mn,s[i]);
    }
    for(mn=0,i=1,p=-1;i<n;++i,p*=-1)
    {
        s[i]=s[i-1]+abs(a[i+1]-a[i])*p;
        mx=max(mx,s[i]-mn);
        if(i&1)mn=min(mn,s[i]);
    }
    printf("%I64d",mx);
}

B. Weird journey

题目大意：给定一张n个点m条边的无向图，无重边，有自环，问有多少对边满足有路径有且只经过这两条边一次，且经过其他m-2条边两次。（n,m<=10^6）

思路：分类讨论+大判断。先判连通性，答案为相邻的非自环边对数+自环边数*非自环边数+自环边对数。

#include<cstdio>
char B[1<<26],*S=B,C;int X;
inline int read()
{
    while((C=*S++)<'0'||C>'9');
    for(X=C-'0';(C=*S++)>='0'&&C<='9';)X=(X<<3)+(X<<1)+C-'0';
    return X;
}
#define MN 1000000
int f[MN+5],r[MN+5],u[MN+5];
int gf(int k){return f[k]?f[k]=gf(f[k]):k;}
int main()
{
    fread(B,1,1<<26,stdin);
    int n,m,x,y,i,cnt=1,s=0;long long ans=0;
    n=read();m=read();
    for(i=1;i<=m;++i)
    {
        x=read();y=read();
        if(x==y)++s,u[x]=1;
        else ++r[x],++r[y];
        if(gf(x)!=gf(y))++cnt,f[gf(x)]=gf(y);
    }
    for(i=1;i<=n;++i)if(!u[i]&&!r[i])++cnt;
    if(cnt<n)return 0*puts("0");
    for(i=1;i<=n;++i)ans+=1LL*r[i]*(r[i]-1)>>1;
    ans+=1LL*s*(m-s)+(1LL*s*(s-1)>>1);
    printf("%I64d",ans);
}

C. The Great Mixing

题目大意：k种可乐，每种浓度为ai/1000，每种取出任意自然数份混合在一起，问混合出浓度为n/1000的可乐至少要几份。（0<=n,ai<=1000，k<=10^6）

思路：先把所有ai减去n，问题转化为选出的和为0至少选几个，如果都小于0或都大于0则无解，否则容易证明答案至多为O(n)（若ai<0，aj>0，则ai*aj+aj*(-ai)=0），bfs搜出和为x至少要几步，可以很快算出答案。

#include<cstdio>
char B[1<<26],*S=B,C;int X;
inline int read()
{
    while((C=*S++)<'0'||C>'9');
    for(X=C-'0';(C=*S++)>='0'&&C<='9';)X=(X<<3)+(X<<1)+C-'0';
    return X;
}
#define MN 1000
#define MX 1000000
int u[MN*2+5],t[MN+5],tn,d[MX*2+5],q[MX*2+5],qn;
int main()
{
    fread(B,1,1<<26,stdin);
    int n,k,i,j,x,o1=1,o2=1;
    n=read();k=read();
    for(i=1;i<=k;++i)
    {
        if(!(x=read()-n))return 0*puts("1");
        if(x<0)o1=0;
        if(x>0)o2=0;
        if(!u[x+MN])u[x+MN]=1,t[++tn]=x;
    }
    if(o1||o2)return 0*puts("-1");
    for(i=1;i<=tn;++i)d[q[++qn]=t[i]+MX]=1;
    for(i=1;i<=qn;++i)
    {
        if(q[i]==MX)return 0*printf("%d",d[MX]);
        for(j=1;j<=tn;++j)
        {
            x=q[i]+t[j];
            if(x<0||x>MX*2||d[x])continue;
            d[q[++qn]=x]=d[q[i]]+1;
        }
    }
}