模拟赛直接升天
100 + 100 + 100 + 30 秒变 50 + 30 + 0 + 30
自身的问题还是有点多
A. 简单游走
有一张 n 个点, m条边的无向图,点从 1到 n标号。
时刻 0时,你在结点1 。你需要用最少的时间从结点 1走到结点n 。通过m条边中的每一条都要花一定的时间。
每个结点会有可能在某些时刻被限制。一个结点 x 在时刻T被限制,意味着这个结点的人在时刻T不能从这个点x走出去。
你只能在整数时刻进出某个结点,一个结点可以逗留任意非负整数时间。
现在,请问你最少需要多少时间能从结点 1走到结点n 。
可以看出肯定越早到一个点越优 在这个点上等再到这个点的所有连点 和 到连点后再等待出点 是同一个道理,我们记录每个点的最早到达时间,
用最早出点时间更新它的连点 跑一遍最短路就行了 同时 数组 需要 开大 且 开始定义的最大值要很大 不然直接wa了。

#include <iostream> #include <cstdio> #include <queue> #include <algorithm> #define f(i, a, b) for (long long i = a; i <= b; i++) using namespace std; priority_queue<pair<long long, long long> > QAQ; long long n, m, k, begi, fina, v, head[100100], d[100100]; bool tim[5000][5000]; bool visit[100010]; struct QWQ { long long to, next, value; } edge[100100]; void make(long long a, long long b, long long c) { edge[++edge[0].value].to = b; edge[edge[0].value].value = c; edge[edge[0].value].next = head[a]; head[a] = edge[0].value; } void dij() { QAQ.push(make_pair(0, 1)); d[1] = 0; while (QAQ.size()) { long long num = QAQ.top().second; QAQ.pop(); if(visit[num]) continue; visit[num] = 1; long long p = d[num]; while(tim[num][p])p++; for (long long i = head[num]; i; i = edge[i].next) { if (p + edge[i].value < d[edge[i].to]) { d[edge[i].to] = p + edge[i].value; QAQ.push(make_pair(-d[edge[i].to], edge[i].to)); } } } } int main() { freopen("travel.in", "r", stdin); freopen("travel.out", "w", stdout); scanf("%lld%lld", &n, &m); f(i, 1, m) { scanf("%lld%lld%lld", &begi, &fina, &v); make(begi, fina, v); make(fina, begi, v); } f(i, 1, n) { scanf("%lld", &k); long long t; f(j, 1, k) { scanf("%lld", &t); tim[i][t] = 1; } d[i] = 1e16; } dij(); printf("%lld", d[n]); return 0; }
B. 卡牌选取
校庆志愿者小Z在休息时间和同学们玩卡牌游戏。一共有n张卡牌,每张卡牌上有一个数Ai,每次可以从中选出k张卡牌。一种选取方案的幸运值为这k张卡牌上数的异或和。小Z想知道所有选取方案的幸运值之和除以998244353的余数。
我们考虑使用二进制 对于 二进制的每一位 只有 奇数个1 异或 才是有意义的 所以我们只要对每一位的数字统计 n 个 0,1 有多少种 k 个 数的组合有奇数个1
(设此为所有的数的的和为sum)此位为第i位 选出 j 个 1 则剩下 k - j 个 0


#include<iostream> #include<cstdio> using namespace std; const long long MOD = 998244353; long long jc[1000000],inv[1000000]; long long n,k,sum,num[1000000],cn[1000000]; long long pow(long long a,long long b) { long long ans = 1; while(b) { if(b & 1) ans = (ans * a )%MOD; a =( a * a )%MOD; b = b >> 1; } return ans; } long long C(long long n,long long m) { if(m > n) return 0; return (jc[n] % MOD * inv[m] % MOD * inv[n-m] % MOD) % MOD; } int main() { freopen("card.in","r",stdin); freopen("card.out","w",stdout); scanf("%lld%lld",&n,&k); for(long long i = 1; i <= n; i++) { scanf("%lld",&num[i]); for(long long j = 0 ;j <= 30; j++) if(num[i] & (1 << j)) cn[j] ++; } jc[0] = inv[0] = jc[1] = 1; for(long long i = 2; i <= n ;i++) jc[i] = (i%MOD * jc[i - 1]%MOD)%MOD; inv[n] = pow (jc[n],MOD - 2)%MOD; for(long long i = n ; i >= 1; i--) inv[i - 1] = (inv[i]%MOD * (i)%MOD)%MOD; inv[1] = 1; for(long long i = 0; i <= 30 ; i++) { long long s = 0; for(long long j = 1 ; j <= k; j += 2) s += ((1LL)*C(cn[i],j)%MOD * C(n - cn[i],k - j)%MOD)%MOD ; sum += ((1LL<<i) %MOD * s%MOD)%MOD; } cout<<sum%MOD; }
 ‘
‘
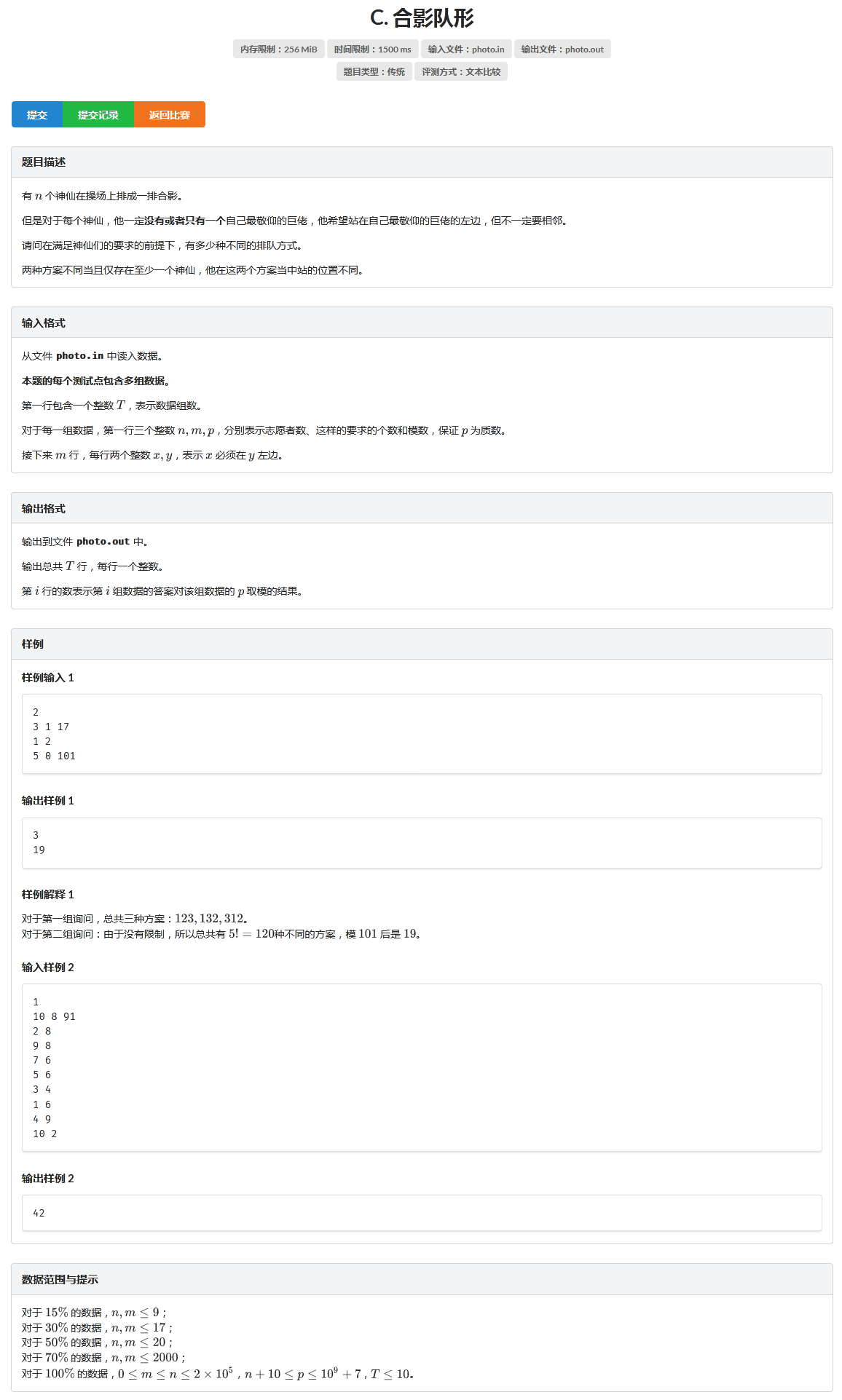
我们将所有的要求变成一颗树,若a要求在b前面,那么a<-b连一条边,若有x没有要求,连一条0->x的边
先判断有没有环,有就直接输出0
没有环,就从0开始dfs,当每个子树的方案都已经求出来后就可以用乘法原理合并了
其实就是每次将一堆节点插入到另一堆中,在乘上子树自己的方案数

#include <algorithm> #include <iostream> #include <cstring> #include <vector> #include <cstdio> #include <cmath> #include <queue> using namespace std; typedef long long LL; inline const LL Get_Int() { LL num = 0, bj = 1; char x = getchar(); while (x < '0' || x > '9') { if (x == '-') bj = -1; x = getchar(); } while (x >= '0' && x <= '9') { num = num * 10 + x - '0'; x = getchar(); } return num * bj; } const int maxn = 200005; int t, n, m, Size[maxn], InDegree[maxn]; LL f[maxn], fac[maxn], inv[maxn], mod; bool bj = 0, vst[maxn]; vector<int> edges[maxn]; void Clear() { memset(InDegree, 0, sizeof(InDegree)); memset(vst, 0, sizeof(vst)); bj = 0; for (int i = 0; i <= n; i++) edges[i].clear(); } void AddEdge(int x, int y) { edges[x].push_back(y); } void Dfs(int Now) { vst[Now] = 1; for (int i = 0; i < edges[Now].size(); i++) { int Next = edges[Now][i]; if (vst[Next]) { bj = 1; return; } Dfs(Next); if (bj) return; } } LL C(LL a, LL b) { return fac[a] * inv[b] % mod * inv[a - b] % mod; } void TreeDp(int Now) { f[Now] = 1; Size[Now] = 0; for (int i = 0; i < edges[Now].size(); i++) { int Next = edges[Now][i]; TreeDp(Next); Size[Now] += Size[Next]; f[Now] = f[Now] * C(Size[Now], Size[Next]) % mod * f[Next] % mod; } Size[Now]++; } LL Quick_Pow(LL a, LL b) { LL ans = 1; while (b) { if (b & 1) ans = ans * a % mod; a = a * a % mod; b >>= 1; } return ans; } int main() { freopen("photo.in", "r", stdin); freopen("photo.out", "w", stdout); t = Get_Int(); while (t--) { n = Get_Int(); m = Get_Int(); mod = Get_Int(); Clear(); fac[0] = inv[0] = 1; for (int i = 1; i <= n + 1; i++) fac[i] = fac[i - 1] * i % mod; inv[n + 1] = Quick_Pow(fac[n + 1], mod - 2); for (int i = n; i >= 1; i--) inv[i] = inv[i + 1] * (i + 1) % mod; for (int i = 1; i <= m; i++) { int x = Get_Int(), y = Get_Int(); AddEdge(y, x); InDegree[x]++; } for (int i = 1; i <= n; i++) if (!InDegree[i]) AddEdge(0, i); for (int i = 0; i <= n; i++) if (!vst[i]) Dfs(i); if (bj) { puts("0"); continue; } TreeDp(0); printf("%lld ", f[0]); } return 0; }

对于第一档数据我们考虑DP DP方程并不难写

#include<iostream> #include<cstdio> #define f(i,a,b) for(long long i = a; i <= b; i++) #define d(i,a,b) for(long long i = a; i >= b; i--) using namespace std; long long n,maxx; long long ans[1000010],c[1000010],v[1000010]; int main() { freopen("bus.in","r",stdin); freopen("bus.out","w",stdout); scanf("%lld%lld",&n,&maxx); f(i,0,n - 1) { scanf("%lld%lld",&c[i],&v[i]); ans[i] = 0x7f7f7f; } ans[n] = 0x7f7f7f; ans[0] = 0; f(i,1,n) { d(j,i-1,0) if((i - j)%c[j] == 0) ans[i] = min(ans[i],ans[j] + (i - j)/c[j]*v[j]); if(ans[i] == 0x7f7f7f) printf("-1 "); else printf("%lld ",ans[i]); } }
我们对于第三档数据 考虑贪心从v最小的转移

#include <bits/stdc++.h> using namespace std; #define ll long long #define re register inline int read() { int num = 0, sym = 1; char ch = getchar(); while (ch < '0' || ch > '9') { if (ch == '-') sym = -1; ch = getchar(); } while ('0' <= ch && ch <= '9') { num = (num << 1) + (num << 3) + (ch ^ 48); ch = getchar(); } return num * sym; } const int maxn = 1e6 + 10; int n, C, c[maxn], v[maxn]; ll f[maxn], ans; int main() { freopen("bus.in", "r", stdin); freopen("bus.out", "w", stdout); n = read(); C = read(); for (int i = 0; i < n; i++) c[i] = read(), v[i] = read(); if (C == 1) { int nu = v[0]; for (int i = 1; i <= n; i++) { ans += nu; nu = min(nu, v[i]); printf("%lld ", ans); } return 0; } memset(f, 0x3f3f3f3f, sizeof(f)); f[0] = 0; for (int i = 1; i <= n; i++) { for (int j = 0; j < i; j++) { if ((i - j) % c[j] == 0 && f[j]!= 0x3f3f3f3f) { f[i] = min(f[i], f[j] + ((i - j) / c[j]) * v[j]); } } if (f[i] >= 0x3f3f3f3f) printf("-1 "); else printf("%lld ", f[i]); } return 0; }
这样可以拿50分 对于其他数据要使用维护凸包(不会 雾)
这里埋个坑
