---恢复内容开始---
题意: t组数据,每组数据给出n个木棒,长度由1到n,除了两端的木棒外,每一根木棒,要么比它左右的两根都长,要么比它左右的两根都短。即要求构成的排列为波浪型。对符合要求的排列按字典序(从左到右,从低到高)进行排序,求排列序号为c的排列。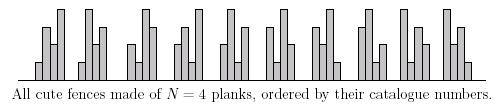
刚拿到这道题时,也是一脸懵逼,感觉起来要用dp,但又不知道从哪里去下手。在网上搜了一下才大概明白。
我们可以先定义状态f[i]表示第i个木棒的合法方案数,我们考虑去转移,怎么从f[i-j]转移到f[i]呢?我们就要考虑第i-j个木棒的长度以及第i个木棒的长度关系,我们把下降的方案称为down,上升的称为up,我们将i根木棒构成的合法集合称为S(i)。
我们在选定x作为第一根木棒之后,去选择第二个木棒y,此时我们要去考虑x,y的长度关系,而在选定y之后我们又要考虑y和下一根木棒长度的关系,并且当方案不符合时我们也不便于去重新选择,此时我们的方程很难进行转移。
我们便可以考虑在此基础上进行细化f[i]=f[i][k] (k=1....i)
我们再定义状态f[i][j]表示集合S(i)中以第j短的木棒为第一个的方案数那么我们便可以写出状态转移方程
f[i][j]= (sum_{m=j}^p) f[i][m] (down) + (sum_{n=1}^q) f[i][n] (up) (p=i-1,q=j-1)
我们发现这个方程仍然不好转移,因为它还是没有拜托前面的约束。我们便可在问题上再进行细分
f[i][j]=f[i][j][down]+f[i][j][up]
f[i][j][[down]表示i根木棒以第j短的木棒为首的下降方案数,我们再去考虑状态转移方程
f[i[[j][down]= (sum_{n=1}^q)f[i-1][n][up]
f[i[[j][up]= (sum_{m=j}^p)f[i-1][m][down]
(p=i-1,q=j-1)
至此我们可以得出一个技巧,当在做dp类型的题目时,状态不好进行转移时我们可以在此基础上增加一维,如blocks,便于转移
至此问题还并没有得到解决,题目要求序列为c的方案,那么我们又改如何去求到呢?我们考虑以第1短的木棒为第一个的方案p(1),若c>p(1)则说明c不在p(1)之中,c减去p(1),我们再去考虑p(2),若还大于,则类推,当c<=p(k)时我们便可确定c在以第k短的木棒为第一根的集合内,我们再去考虑第二根,以此类推下去,求得解。
代码
#include<bits/stdc++.h>
using namespace std;
int T,n,used[25];
long long f[25][25][2],c;//0->up,1->down
void sta(int n){
memset(f,0,sizeof(f));
f[1][1][0]=f[1][1][1]=1;
for(int i=2;i<=n;++i){
for(int j=1;j<=i;++j){
for(int M=j;M<i;++M) f[i][j][0]+=f[i-1][M][1];
for(int N=1;N<j;++N) f[i][j][1]+=f[i-1][N][0];
}
}
}
void print(int n,long long cc){
long long jump=0;
int a[25];
memset(used,0,sizeof(used));
for(int i=1;i<=n;++i){
long long tmp=jump;
int k,p=0;
for(k=1;k<=n;++k){
tmp=jump;
if(!used[k]){
++p;
if(i==1) jump+=f[n][p][1]+f[n][p][0];
else{
if(k>a[i-1]&&(i<=2||a[i-2]>a[i-1])) jump+=f[n-i+1][p][1];
if(k<a[i-1]&&(i<=2||a[i-2]<a[i-1])) jump+=f[n-i+1][p][0];
}
if(jump>=cc) break;
}
}
used[k]=1;
a[i]=k;
jump=tmp;
}
for(int i=1;i<=n;++i){
printf("%d ",a[i]);
if(i==n) printf("
");
}
}
int main(){
scanf("%d",&T);
sta(20);
while(T--){
scanf("%d %lld",&n,&c);
print(n,c);
}
return 0;
}
---恢复内容结束---