https://vjudge.net/contest/262670#problem/B
线段树
https://vjudge.net/contest/230809#problem/T
题目链接。后面两题比较难。
add与sum操作的时间复杂度都是logn的,(和二分有点相似,在时间复杂度方面),如果预处理执行n次add操作的话就是nlogn的复杂度。
https://blog.csdn.net/qq_37685156/article/details/79822314
树状数组,乒乓球比赛类似于求逆序数,好像可以用归并法来做,训练之南上的
https://blog.csdn.net/lin375691011/article/details/21247409
二维树状数组
https://www.cnblogs.com/whatbeg/p/3970310.html
三维树状数组,如果是01取反的话,在1的基础上加1与-1是一样的。
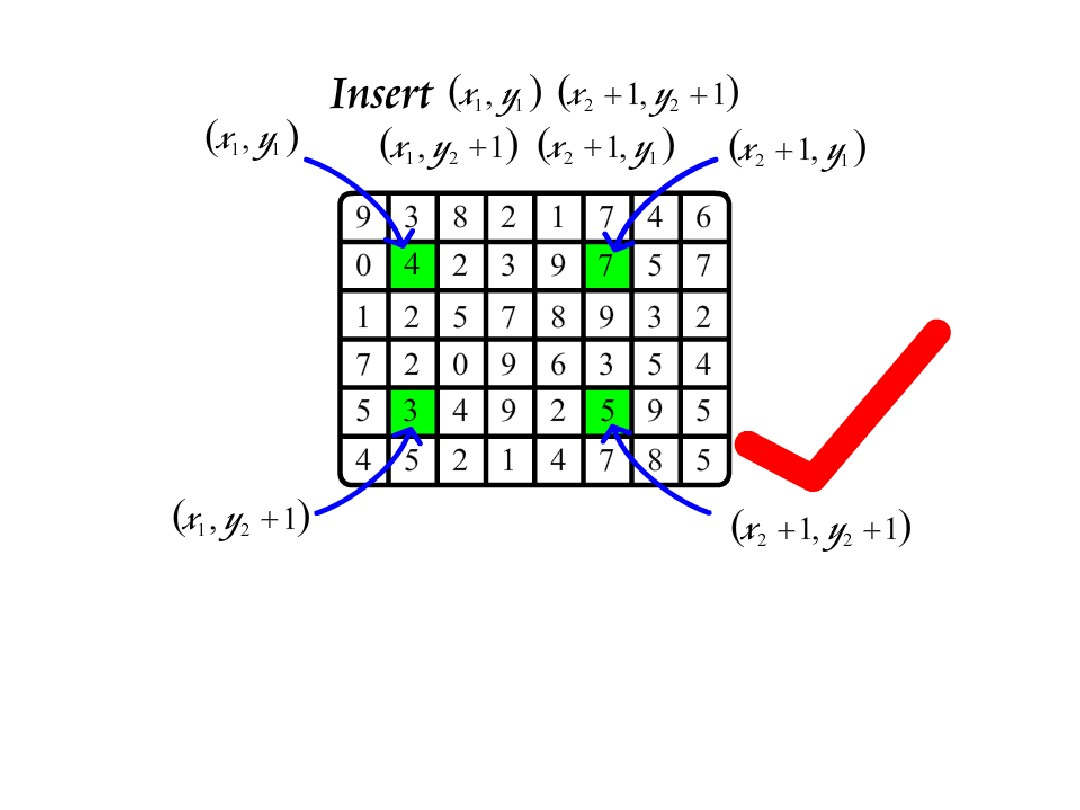
二维区间修改的图。
Matrix
差分
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int T,n,m,bit[1005][1005]; char s[10]; int sum(int a,int b) { int s = 0; for(int i=a;i>0;i-=i&-i) for(int j=b;j>0;j-=j&-j) s+=bit[i][j]; return s; } void add(int a,int b) { for(int i=a;i<=n;i+=i&-i) for(int j=b;j<=n;j+=j&-j){ bit[i][j]++; } } int main() { scanf("%d",&T); while(T--) { scanf("%d%d",&n,&m); memset(bit,0,sizeof(bit)); while(m--) { scanf("%s",s); if(s[0]=='C'){ int x1,y1,x2,y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2); add(x2+1,y2+1); add(x1,y1); add(x1,y2+1); add(x2+1,y1); } else { int x,y; scanf("%d%d",&x,&y); printf("%d ",sum(x,y)%2); } } if(T) printf(" "); } return 0; }
https://blog.csdn.net/qq_39826163/article/details/89450013
【题意】
在一个面积不超过n*m的矩形上,有p个矩形A,问之后的q个矩形B能否被之前的A全部覆盖(每个B的点都在至少一个A中)。
【解题思路】
对于A类矩形(x1,y1,x2,y2),我们只需要在(x1,y1),(x2+1,y2+1)处+1,在(x1,y2+1)(x2+1,y1)处-1。
之后对整个面积求一个前缀和。则大于0的地方就是被A类矩形覆盖的点。 把值大于0的地方变成1,再一次求一次前缀和,处理好后即可在O(1)的时间算出一个矩形内被覆盖的点的数量。
需要注意的是因为n*m<10^7,所以需要把二维转换成一维来做。
重点是把二维的树状数组转成一维的
#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=1e7+500; LL a[maxn],s[maxn]; int n,m,p,q; int lowbit(int x) { return (-x)&x; } void add(int x,int y,int z) { int ty=y; while(x<=n) { y=ty; while(y<=m) { a[x*m+y]+=z; y+=lowbit(y); } x+=lowbit(x); } } LL query(int x,int y) { LL sum=0; int ty=y; while(x) { y=ty; while(y) { sum+=a[x*m+y]; y-=lowbit(y); } x-=lowbit(x); } return sum; } int main() { while(~scanf("%d%d",&n,&m)) { memset(a,0,sizeof(a)); memset(s,0,sizeof(s)); int x1,y1,x2,y2; scanf("%d",&p); while(p--) { scanf("%d%d%d%d",&x1,&y1,&x2,&y2); add(x1,y1,1); add(x1,y2+1,-1); add(x2+1,y1,-1); add(x2+1,y2+1,1); } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { int t=query(i,j); if(t>0)s[i*m+j]=1; else s[i*m+j]=0; } } for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) s[i*m+j]+=s[(i-1)*m+j]+s[i*m+j-1]-s[(i-1)*m+j-1]; } scanf("%d",&q); while(q--) { scanf("%d%d%d%d",&x1,&y1,&x2,&y2); LL t1=(x2-x1+1)*(y2-y1+1); LL t2=s[x2*m+y2]+s[(x1-1)*m+y1-1]-s[(x1-1)*m+y2]-s[x2*m+y1-1]; if(t1==t2)printf("YES "); else printf("NO "); } } }
https://wenku.baidu.com/view/402b20d0162ded630b1c59eef8c75fbfc67d9479.html
浅谈信息学竞赛中的0和1.
https://blog.csdn.net/getsum/article/details/51316927
一个异或的题。
https://blog.csdn.net/qq_39562952/article/details/81298043
区间更新与区间查询。
https://blog.csdn.net/weizhuwyzc000/article/details/45442815/
二维的区间更新,与一维有点不同。
查找第几个比i大的值可以用二分。注意判断某一位是否为零必须是sum[i] - sum[i - 1] == 0 而不是直接判那一位是否为零,因为bit[i]指的是他管辖的范围内的值得总和。
注意当给一个矩形对角线坐标时,要判大小,小的放在一起,大的放在一起(可能会要换一条对角线,为了让二维树状数组好算)。
一般为了防止为零都会加一。
有时候要把sum的值用long long 存。
离散化后add是就是n,没离散化就是maxm.
用二分的时候范围记得搞大点。
1.预处理,输入并离散化处理
void init() { for(int i=1;i<=n;i++)//输入n个数(1-n) { scanf("%d",&d[i].v); d[i].ord=i; } sort(d+1,d+n+1,cmp1); for(int i=1;i<=n;i++) { b[d[i].ord]=i; } }
成对数据离散化
struct node { ll x, y, xx, yy; } p[maxm]; sort(p + 1, p + 1 + n, comp1); p[1].x = 1; for(int i = 2; i <= n; i++) { if(p[i].xx == p[i - 1].xx) { p[i].x = p[i - 1].x; } else p[i].x = i; } sort(p + 1, p + n + 1, comp2); p[1].y = 1; for(int i = 2; i <= n; i++) { if(p[i].yy == p[i - 1].yy) { p[i].y = p[i - 1].y; } else p[i].y = i; }
离散化处理。
2.一维前缀和与改变值
int lowbit(int x) { return x & -x; } void add(int i, int x) { while(i <= 32005) {//如果离散化的话就是n,没离散化就是maxm. bit[i] += x; i += lowbit(i); } } int sum(int i) { int s = 0; while(i > 0) { s += bit[i]; i -= i & -i; } return s; }
//注意先sum后add或者先add后sum.
3.二维
Mobile phones
int lowbit(int x) {
return x & -x;
}
void add(int x, int y, int a) {
for(int i = x; i <= n; i += lowbit(i)) {
for(int j = y; j <= n; j += lowbit(j)) {
bit[i][j] += a;
}
}
}
int sum(int x, int y) {
int s = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
for(int j = y; j > 0; j -= lowbit(j)) {
s += bit[i][j];
}
}
return s;
}
sum(l2, r2) + sum(l1 - 1, r1 - 1) - sum(l2, r1 - 1) - sum(l1 - 1, r2)//一个矩形
三维线状数组
int c[maxn][maxn][maxn]; int lowbit(int x){ return x&(-x); } void add(int x,int y,int z, int a) { for(int i=x;i<=maxn;i+=lowbit(i)) { for(int j=y;j<=maxn;j+=lowbit(j)) { for(int k=z;k<=maxn;k+=lowbit(k)) { c[i][j][k] += a; } } } } int getsum(int x,int y,int z) { int sum=0; for(int i=x;i>0;i-=lowbit(i)) { for(int j=y;j>0;j-=lowbit(j)) { for(int k=z;k>0;k-=lowbit(k)) { sum+=c[i][j][k]; } } } return sum; }
树状数组求区间最大值模板
专题结束在补
https://vjudge.net/contest/293001#problem/H Gym - 100971H
Description
一个人想邀请k个朋友来做客,给第i个朋友打电话他会告诉一个[ai,bi]表示包括这个人自己在内有ai到bi个人去这个人就会去,每次打电话都是从第一个朋友开始按顺序打,叫够k个人就不打电话了,问对1~n中每个k要打多少个电话恰能邀请到k个人
Input
第一行一整数n表示朋友数量,之后n行两个整数ai和bi表示该朋友去做客对人数的要求(1<=n<=2e5,1<=ai<=bi<=n)
Output
输出n个数表示k从1取到n时至少需要打多少电话才能叫到k个人,如果给n个人打电话后也叫不齐k个人则输出-1
Sample Input
6
3 3
1 2
3 6
3 4
1 4
4 6
Sample Output
2 5 4 6 -1 -1
解法 :树状数组,按区间值来排序,有点类似于差分,当邀一人时,就把所有可以为一的加到bit上去,两人时就接着邀。然后二分找值。
#include<bits/stdc++.h> using namespace std; const int maxm = 2e5 + 5; int bit[maxm]; int n; int res[maxm]; struct Node { int ind, v, flag; bool operator < (const Node &a) const { return v < a.v; } Node(int ind = 0, int v = 0, int flag = 0) : ind(ind), v(v), flag(flag) {}; }node[maxm * 2]; int lowbit(int x) { return x & -x; } void add(int x, int val) { while(x <= n) { bit[x] += val; x += lowbit(x); } } int sum(int x) { int s = 0; while(x > 0) { s += bit[x]; x -= lowbit(x); } return s; } int main() { scanf("%d", &n); int ql, qr; for(int i = 1; i <= n; i++) { scanf("%d%d", &ql, &qr); node[2 * i - 1] = Node(i, ql, 1); node[2 * i] = Node(i, qr + 1, -1); } sort(node + 1, node + 2 * n + 1); int r = 1; for(int i = 1; i <= n; i++) { while(r <= 2 * n && node[r].v <= i) { add(node[r].ind, node[r].flag); r++; } int ml = 1, mr = n, ans = n + 1, mid; while(ml <= mr) { mid = (ml + mr) >> 1; if(sum(mid) >= i) { if(sum(mid) == i) { ans = min(ans, mid); } mr = mid - 1; } else { ml = mid + 1; } } res[i] = (ans == n + 1) ? -1 : ans; } for(int i = 1; i <= n; i++) { printf("%d%c", res[i], i == n ? ' ' : ' '); } return 0; }
Cows
POJ - 2481这个在排序的时候要注意一下。
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; int bit[100005], n, res[100005]; struct node{ int l, r, index; } p[100005]; int lowbit(int x) { return x & -x; } void add(int i, int x) { while(i <= 100005) { bit[i] += x; i += lowbit(i); } } int sum(int i) { int s = 0; while(i > 0) { s += bit[i]; i -= lowbit(i); } return s; } int comp(node p1, node p2) { if(p1.r == p2.r) return p1.l < p2.l; return p1.r > p2.r; } int main() { while(~scanf("%d", &n) && n) { memset(res, 0, sizeof(res)); memset(bit, 0, sizeof(bit)); for(int i = 1; i <= n; i++) { scanf("%d%d", &p[i].l, &p[i].r); p[i].l++; p[i].r++; p[i].index = i; } sort(p + 1, p + 1 + n, comp); res[ p[1].index ] = 0; add(p[1].l, 1); for(int i = 2; i <= n; i++) { if(p[i].l == p[i - 1].l && p[i].r == p[i - 1].r) { //如果区间相等 res[ p[i].index ] = res[ p[i - 1].index ]; } else { res[ p[i].index ] = sum(p[i].l); } add(p[i].l, 1); } for(int i = 1; i <= n; i++) { if(i == 1) { printf("%d", res[1]); } else printf(" %d", res[i]); } printf(" "); } return 0; }
Apple Tree
POJ - 3321 涉及到dfs序的一道题目
https://www.cnblogs.com/gj-Acit/p/3236843.html
dfs序两个数组记录的是他子树节点的最大值与最小值。
#include<cstdio> #include<algorithm> #include<cstring> #include<vector> using namespace std; const int maxm = 1e5 + 5; int bit[maxm], in[maxm], out[maxm], n, m, fork[maxm], ans; vector< vector<int> >edge(maxm); int lowbit(int x) { return x & -x; } int sum(int i) { int s = 0; while(i > 0) { s += bit[i]; i -= lowbit(i); } return s; } void add(int i, int x) { while(i <= maxm) { bit[i] += x; i += lowbit(i); } } void dfs(int u) { in[u] = ans; for(int i = 0; i < edge[u].size(); i++) { ans++; dfs(edge[u][i]); } out[u] = ans; } int main() { scanf("%d", &n); int a = 0, b = 0; ans = 1; for(int i = 1; i < n; i++) { scanf("%d%d", &a, &b); edge[a].push_back(b); } for(int i = 1; i <= n; i++) { fork[i] = 1; add(i, 1); } dfs(1); scanf("%d", &m); for(int i = 0; i < m; i++) { char ch[3]; int t = 0; scanf("%s", ch); scanf("%d", &t); if(ch[0] == 'Q') { printf("%d ", sum(out[t]) - sum(in[t] - 1)); } else { if(fork[t]) { add(in[t], -1); } else { add(in[t], 1); } fork[t] = !fork[t]; } } return 0; }
MooFest
POJ - 1990 好题
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; typedef long long int64; const int MAXN = 20010; struct Node{ int x; int v; }; Node node[MAXN]; int n; int treeCount[MAXN]; int treeDis[MAXN]; int comp(Node n1, Node n2) { return n1.v < n2.v; } int lowbit(int x){ return x&(-x); } int64 getSum(int x , int arr[]){ int64 sum = 0; while(x){ sum += arr[x]; x -= lowbit(x); } return sum; } void add(int x , int val , int arr[]){ while(x <= MAXN){ arr[x] += val; x += lowbit(x); } } int64 solve(){ int64 ans = 0; int64 totalDis = 0; memset(treeCount , 0 , sizeof(treeCount)); memset(treeDis , 0 , sizeof(treeDis)); sort(node + 1 , node+n + 1, comp); for(int i = 1 ; i <= n ; i++){ int64 count = getSum(node[i].x , treeCount); int64 dis = getSum(node[i].x , treeDis); // left ans += node[i].v*(count*node[i].x-dis); // right ans += node[i].v*(getSum(MAXN, treeDis)-dis-(i - 1-count)*node[i].x); // update totalDis += node[i].x; add(node[i].x , 1 , treeCount); add(node[i].x , node[i].x , treeDis); } return ans; } int main(){ while(scanf("%d" , &n) != EOF){ for(int i = 1 ; i <= n ; i++) scanf("%d%d" , &node[i].v , &node[i].x); printf("%lld " , solve()); } return 0; }
KiKi's K-Number
HDU - 2852 涉及二分,好题
#include<cstdio> #include<algorithm> #include<cstring> using namespace std; typedef long long ll; const int maxm = 1e5 + 5; int n, T, x, a, b; ll bit1[maxm], bit2[maxm]; int lowbit(int x) { return x & -x; } ll sum(int i, ll a[]) { ll s = 0; while(i) { s += a[i]; i -= lowbit(i); } return s; } void add(int i, int x, ll a[]) { while(i <= maxm) { a[i] += x; i += lowbit(i); } } int main() { while(~scanf("%d", &T)) { memset(bit1, 0, sizeof(bit1)); // res = 0; for(int i = 1; i <= T; i++) { scanf("%d", &n); if(n == 0) { scanf("%d", &a); add(a, 1, bit1); // printf("%d ", sum(maxm, bit1)); } else if(n == 1) { scanf("%d", &a); if(sum(a, bit1) - sum(a - 1, bit1) == 0) { printf("No Elment! "); } else { add(a, -1, bit1); } } else { scanf("%d%d", &a, &b); if(sum(maxm, bit1) - sum(a, bit1) < b) { printf("Not Find! "); } else { int l = a, r = maxm + 1, res = 0, pp = a;; while(l <= r) { int mid = (l + r) / 2; // printf("%d ", mid); if(sum(mid, bit1) - sum(pp, bit1) >= b){ r = mid - 1; res = mid; // printf("%d ", sum(mid, bit1)); } else { l = mid + 1; } } printf("%d ", res); } } } } return 0; }
Necklace
HDU - 3874 线段树离线操作
#include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<iostream> using namespace std; const int maxn = 1e6+10; typedef long long LL; int a[50000+10]; LL ans[200000+10]; LL s[maxn]; int last[maxn];//记录值的位置 int n,m; struct ss{ int x,y,z; bool operator < (const ss &p){ return y<p.y; } }q[200000+10]; int lowbit(int x){ return x&-x; } void add(int x, int v){ while(x<=n){ s[x] += v; x += lowbit(x); } } LL sum(int x){ LL ans = 0; while(x>0){ ans += s[x]; x -= lowbit(x); } return ans; } int main(){ int t; scanf("%d", &t); while(t--){ memset(s,0,sizeof(s)); memset(last,0,sizeof(last)); scanf("%d", &n); for(int i = 1; i <= n; ++i){ scanf("%d",&a[i]); add(i,a[i]); if(!last[a[i]]) last[a[i]] = i;//初始化每个值第一次出现的位置 }scanf("%d", &m); for(int i = 1; i <= m; ++i){ scanf("%d %d", &q[i].x, &q[i].y); q[i].z = i; }sort(q + 1, q + 1 + m); int l = 1; for(int i = 1; i <= m; ++i){ for(int j = l; j <= q[i].y ;++j) if(last[a[j]] != j){//如果值不在当前位置,那么就删去 add(last[a[j]], -a[j]); last[a[j]] = j;//更新值为当前位置 } l = q[i].y; ans[q[i].z] = sum(q[i].y) - sum(q[i].x - 1); } for(int i = 1; i <= m; ++i) printf("%lld ",ans[i]); } return 0; }
1:单点修改:
void update(int x,int v)//单点修改(x节点加上v)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=v;
}
2:前缀和:
int sum(int x)//sum[1,x]
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))
ans+=c[i];
return ans;
}
3:区间修改,单点求值(差分思想)
int solve(int l,int r,int v,int x)//[l,r]区间同时加上v,同时求x节点值(这时转化为求前缀和)
{
c[l]+=v;
c[r+1]-=v;
return sum(x);
}
4:区间修改,区间求和(差分思想,辅助数组)
int solve(int l,int r,int v)//[l,r]同时增加v,同时求得[l,r]区间和
{
for(int i=1;i<=n;i++){
cin>>a[i];
update(diff,i,a[i]-a[i-1]);
update(aux,i,(i-1)*(a[i]-a[i-1]));
}
l--;
int sumr=r*sum(diff,r)-sum(aux,r);
int suml=l*sum(diff,l)-sum(aux,l);
return sumr-suml;
}
5:区间最大最小值
void update(int x)//更改节点值
{
for(int i=x;i<=n;i+=lowbit(i)){//将所有x能影响到的节点更新
h[i]=a[i];//首先取原数组值
for(int j=1;j<lowbit(i);j<<=1){//在子节点中寻求最优值
h[i]=max(h[i],h[i-j]);
}
}
}
int querymax(int l,int r)//区间最大值
{
int ans=0;
while(r>=l){
for(;r-lowbit(r)>=l;r-=lowbit(r))//找到该节点所示的区间包含于[x,y],可直接取根节点最优值
ans=max(ans,h[r]);
ans=max(ans,a[r]);//取当前区间右端点,下一步进行[x,y-1]区间寻找
r--;
}
return ans;
}
6:二维树状数组
void update(int x,int y,int v)//[x,y]值更新
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
c[i][j]+=v;
}
int sum(int x,int y)//[1,1]到[x,y]子矩阵前缀和
{
int ans=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
ans+=c[i][j];
return ans;
}
int solve(int x1,int y1,int x2,int y2)//求该子矩阵区间和
{
return sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1);
}
