——————————————————————————————歌颂这种平凡，一两句唱不完。
http://acm.hdu.edu.cn/showproblem.php?pid=2546 饭卡
题意：给你n个菜的价格，每种菜只能买一次，再给你一个m，表示你卡上的余额，有个规定，就是可以用卡里最后的5元钱去购买所有菜里面最贵的一个菜，问你卡里面最少还剩多少钱。
分析：首先贪心的先用5元钱，去买最贵的那一个菜，然后剩余的钱做一个01背包即可，哦对了，如果一开始的钱就小于5元的话就直接输出即可。
codes: 01背包+贪心
#include<bits/stdc++.h> using namespace std; const int N=1e3+10; int dp[N],a[N]; int main() { ios_base::sync_with_stdio(0); int n,V; while(cin>>n&&n) { memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++) cin>>a[i]; cin>>V; if(V<5) cout<<V<<endl; else { sort(a+1,a+n+1); for(int i=1;i<n;i++) { for(int j=V-5;j>=a[i];j--) { dp[j]=max(dp[j],dp[j-a[i]]+a[i]); } } cout<<V-dp[V-5]-a[n]<<endl; } } return 0; }
Bone collecor:http://acm.hdu.edu.cn/showproblem.php?pid=2602
最裸的01背包：
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?
#include<bits/stdc++.h> using namespace std; const int N=1e3+10; int w[N],v[N],dp[N];// 空间，价值，价值 int main() { int T;cin>>T; while(T--) { memset(dp,0,sizeof(dp)); int n,V;cin>>n>>V; for(int i=1;i<=n;i++) cin>>v[i]; for(int i=1;i<=n;i++) cin>>w[i]; for(int i=1;i<=n;i++) { for(int j=V;j>=w[i];j--) dp[j]=max(dp[j],dp[j-w[i]]+v[i]); } cout<<dp[V]<<endl; } return 0; }
_____________________________大多数人最值得为之不断奋斗的，是梦想而非爱情。_______________________________________________________________________________________
1 01背包问题
1.1 题目
有N件物品和一个容量为V的背包。放入第i件物品耗费的空间是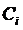
，得到的价值是
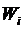。求解最大将哪些物品装入背包可使价值总和。
1.2 基本思路
这是最基本的背包问题，特点是：每种物品仅有一件，可以选择放或不放。
用子问题定义状态:即 f(i,v) 表示前 i 件物品放入一个容量为 v 的背包可以获得的最大价值。则其状态转移方程便是：
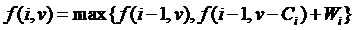
这个方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。所以有必要将它详细解释一下:"将前i件物品放入容量为v的背包中"这个子问题，若只考虑第i件的策略（放或不放），
那么就可以转化为一个只和前 i-1 件物品相关的问题。如果不妨第 i 件物品，那么问题就转化为"前 i-1 件物品放入容量为v 的背包中" ，价值为 f(i-1,v) ;如果放第 i 件物品，那么问题就转化为
"前 i-1 件物品放入容量为 v - C(i) 的背包中 "，此时能获得的最大价值就是 f( i-1, v-C(i) )再加上通过放入第 i 件物品获得的价值 W(i) .
伪代码如下:
f[0,0...V]=0// f[0,0]=0,...f[0,V]=0 for i=1 to N for v=C[i] to V f[i,v] = max{f[i-1,v],f[i-1,v-C[i]]+W[i]}
1.3 优化空间复杂度
以上方法的时间和空间复杂度均为 O(VN)，其中的时间复杂度应该已经不能再优化了，但空间复杂度却可以优化到 O(V)。
先考虑上面的讲的基本思路如何实现，肯定是有一个主循环 i = 1...N, 每次算出来二维数组 f[ i,0 ... V ] 的所有值。那么如果只用一个数组 f[0...V], 能不能保证第i 次循环结束后 f[v] 所表示的值就是我们
所定义的状态 f[i,v] 呢？f[i,v] 是由 f[i-1,v]和f[i-1,v-C[i]]两个子问题递推而来，能否保证在推 f[i, v]时 （也即在第i 次循环中推f[v]时）能够取用 f[i-1,v]和f[i-1, v-C[i]]呢？事实上，这要求在每次主循环中我们
以 v=V... 0 的递减顺序计算 f[v]，这样才能保证推 f[v] 时f[ v-C[i] ]保存的是状态 f[i-1, v-C[i]] 的值。
伪代码如下：
f[0...V]=0 for i=1 to N for v=V to C[i] f[v]=max{f[v],f[v-C[i]]+W[i]}
其中的f[v]=max{f[v] , f[v-C[i]]+W[i] }一句，恰就对应于我们原来的转移方程，因为现在的f[v-C[i]]就相当于原来的 f[i-1,v-C[i]] .
事实上，使用一维数组解 01背包的程序在后面会被多次用到，所以在这里抽象出一个处理一件01背包中的物品过程。
def ZeroOnePack(f,C,W) for v=V to C f[v]=max(f(v),f(v-C)+W)
有了这个过程以后，01背包问题的伪代码就可以这样写:
for i=1 to N ZeroOnePack(f,C,W)
1.4 初始化的细节问题
我们看到的求最优解的背包问题题目中，事实上有两种不太相同的问法。有的题目要求”恰好装满背包“时的最优解，有的题目则并没有要求把背包装满。一种区别这两种问法的实现方法是在初始化的时候有所不同。
1.5 一个常数优化
1.6 小结
01背包问题是最基本的背包问题，它包含了背包问题的设计状态,方程的最基本思想。另外，别的类型的背包问题往往可以转换成01背包问题求解。
故一定要仔细体会上面基本思路的得出方法，状态转移方程的意义，以及空间复杂度怎样被优化。
___________________________________________________________________________________________________________________________________________________________________________
Resources:
https://blog.csdn.net/nobleman__/article/details/78128318