1. 两者区别
约定:在本文中用 LCStr 表示最长公共子串(Longest Common Substring),LCSeq 表示最长公共子序列(Longest Common Subsequence)。
子串要求在原字符串中是连续的,而子序列则没有要求。例如:
字符串 s1=abcde,s2=ade,则 LCStr=de,LCSeq=ade。
2. 求最长公共子串(LCStr)
算法描述:构建如下图的矩阵dp[][],当s1[i] == s2[j] 的时候,dp[i][j]=1;最后矩阵中斜对角线上最长的“1”序列的长度,就是 LCStr 的长度。
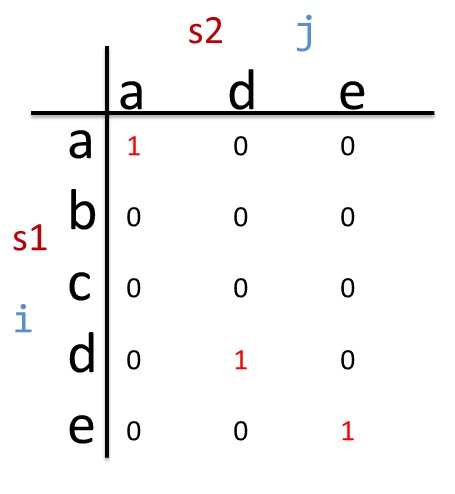
但是求矩阵里斜线上的最长的“1”序列,仍然略显麻烦,我们进行如下优化:当要往矩阵中填“1”的时候,我们不直接填“1”,而是填“1”+左上角的那个数。如下图所示:

这样,我们只需求出矩阵里的最大数(注意:最大数可不一定在最右下角,别误解了上图),即是 LCStr 的长度。
要求出这个 LCStr,其他的不多说了,见代码中注释。
C++ code:

1 #include <iostream> 2 #include <string> 3 #include <cstdlib> // freopen 4 #include <cstring> // memset 5 using namespace std; 6 7 #define MAXN 2001 8 static int dp[MAXN][MAXN]; 9 10 string LCStr(const string &s1, const string &s2) 11 { 12 string result; 13 14 //s1纵向,s2横向 15 //len1行,len2列 16 int len1=s1.length(), len2=s2.length(); 17 memset(dp,0,sizeof(dp)); 18 19 //预先处理第一行第一列 20 for(int i=0; i<len2; ++i) 21 if(s1[0]==s2[i]) dp[0][i]=1; 22 for(int i=0; i<len1; ++i) 23 if(s1[i]==s2[0]) dp[i][0]=1; 24 25 for(int i=1; i<len1; ++i) 26 for(int j=1; j<len2; ++j) 27 if(s1[i]==s2[j]) dp[i][j]=dp[i-1][j-1]+1; //矩阵填充 28 29 //将第一行的最大值移到最右边 30 for(int i=1; i<len2; ++i) 31 if(dp[0][i]<dp[0][i-1]) dp[0][i]=dp[0][i-1]; 32 33 //从第二行开始,将每一行的最大值移到最右边 34 //最后边的数和上一行的最右边数比较大小,将大的下移 35 //到最后,右下角的数就是整个矩阵的最大值 36 for(int i=1; i<len1; ++i) 37 { 38 for(int j=1; j<len2; ++j) 39 if(dp[i][j]<dp[i][j-1]) dp[i][j]=dp[i][j-1]; 40 if(dp[i][len2-1]<dp[i-1][len2-1]) dp[i][len2-1]=dp[i-1][len2-1]; 41 } 42 cout<<"length of LCStr: "<<dp[len1-1][len2-1]<<endl; 43 44 int max = dp[len1-1][len2-1]; 45 int pos_x; 46 for(int i=0; i<len1; ++i) 47 for(int j=0; j<len2; ++j) 48 { 49 if(dp[i][j]==max) 50 { 51 pos_x=i; 52 j=len2; /// 53 i=len1; ///快速跳出循环 54 } 55 } 56 result=s1.substr(pos_x-max+1,max); 57 return result; 58 } 59 60 int main() 61 { 62 int t; 63 freopen("in.txt","r",stdin); 64 cin>>t; 65 cout<<"total tests: "<<t<<endl<<endl; 66 while(t--) 67 { 68 string a,b; 69 cin>>a>>b; 70 cout<<a<<endl<<b<<endl; 71 72 string res=LCStr(a,b); 73 cout<<"LCStr: "<<res<<endl<<endl; 74 } 75 return 0; 76 }
运行:
输入:
5
abcde
ade
flymouseEnglishpoor
comeonflymouseinenglish
BCXCADFESBABCACA
ABCACADF
programming
contest
123454567811267234678392
1457890567809713265738
输出:

3. 最长公共子序列(LCSeq)
算法描述:

矩阵最后的 dp[i][j] 就是 LCSeq 的长度。
为了把 LCSeq 求出来,我们在给每一个 dp[i][j] 赋值的时候,需要记住这个值来自于哪里。是来自于左上角(LEFTUP),还是上边(UP),还是左边(LEFT)。然后从矩阵最后一个元素回溯,就能找出 LCSeq。如下图:
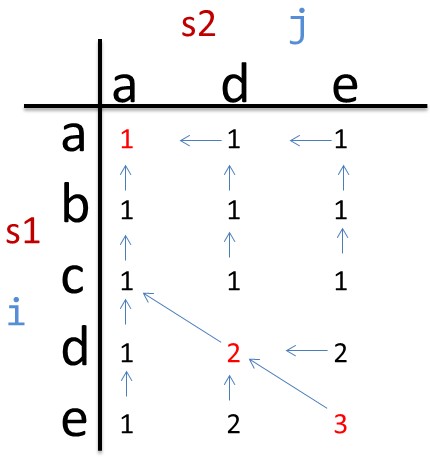
当 dp[i-1][j]==dp[i][j-1],即左边的元素等于上边的元素时,我取上边的元素。(取左边的也行,并不影响程序结果。但在整个代码中要统一规则)。
C++ code:

1 #include <iostream> 2 #include <string> 3 #include <cstring> //memset 4 #include <algorithm> //reverse 5 #define LEFTUP 0 6 #define UP 1 7 #define LEFT 2 8 #define MAXN 2001 9 using namespace std; 10 11 //s1纵向,s2横向 12 int dp[MAXN][MAXN]; 13 short path[MAXN][MAXN]; 14 string LCSeq(const string &s1, const string &s2) 15 { 16 int len1=s1.length(), len2=s2.length(); 17 string result=""; 18 19 //将dp[][]和path[][]的首行首列清零 20 for(int j=0; j<=len2; ++j) 21 {dp[0][j]=0; path[0][j]=0;} 22 for(int i=0; i<=len1; ++i) 23 {dp[i][0]=0; path[i][0]=0;} 24 //以上代码用 memset 也行 25 //memset(dp,0,sizeof(dp)); 26 //memset(path,0,sizeof(path)); 27 28 for(int i=1; i<=len1; ++i) 29 { 30 for(int j=1; j<=len2; ++j) 31 { 32 if(s1[i-1]==s2[j-1]) 33 { 34 dp[i][j]=dp[i-1][j-1]+1; 35 path[i][j]=LEFTUP; 36 } 37 else if(dp[i-1][j]>dp[i][j-1]) //up>=left 这里是用 > 还是 >= ,当LCS不唯一时,对结果有影响,但长度一样 38 { 39 dp[i][j]=dp[i-1][j]; 40 path[i][j]=UP; 41 } 42 else 43 { 44 dp[i][j]=dp[i][j-1]; 45 path[i][j]=LEFT; 46 } 47 } 48 } //矩阵填充完成 49 cout<<"length of LCSeq: "<<dp[len1][len2]<<endl; 50 51 int i=len1, j=len2; 52 while(i>0 && j>0) 53 { 54 if(path[i][j]==LEFTUP) 55 { 56 result+=s1[i-1]; 57 i--; 58 j--; 59 } 60 else if(path[i][j]==UP) i--; 61 else if(path[i][j]==LEFT) j--; 62 } 63 reverse(result.begin(), result.end()); 64 return result; 65 } 66 67 int main() 68 { 69 int t; 70 freopen("in.txt", "r", stdin); 71 //freopen("out.txt", "w", stdout); 72 cin>>t; 73 cout<<"total tests: "<<t<<endl<<endl; 74 while(t--) 75 { 76 string s1,s2; 77 cin>>s1>>s2; 78 cout<<s1<<endl<<s2<<endl; 79 80 string res=LCSeq(s1,s2); 81 cout<<"LCSeq: "<<res<<endl<<endl; 82 83 } 84 return 0; 85 } 86 87
运行:
输入:同上
输出:
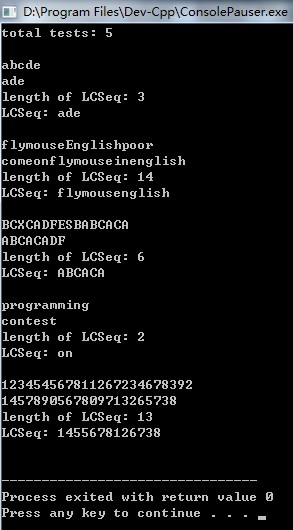
说一下以上程序中37行的 >= 和 > 的区别。当 LCSeq 不唯一时,讨论此区别才有意义。对于以下两个字符串
s1=BCXCADFESBABCACA , s2=ABCACADF
取>=和>符号时的求得的LCSeq分别为:
BCCADF 和 ABCACA
【s1=BCXCADFESBABCACA , s2=ABCACADF】
【s1=BCXCADFESBABCACA , s2=ABCACADF】
分析:
当取>=符号时,就是说当dp[i][j]上边的数与左边的数相等时,选择上边的数赋给dp[i][j]。这就造成在后来的回溯过程中,回溯的路径“更快地往上走,更慢的往左走”,当回溯结束时,所求的的子序列由“s2的靠后部分 + s1的靠前部分”构成。(这里的“靠前”、“靠后”为相对而言)。
当取>符号时,就是说当dp[i][j]上边的数与左边的数相等时,选择左边的数赋给dp[i][j]。这就造成在后来的回溯过程中,回溯的路径“更快地往左走,更慢的往上走”,当回溯结束时,所求的的子序列由“s1的靠后部分 + s2的靠前部分”构成。
可以参看上面的图来理解这个过程,也可自己画两个图试一下。
参考:
维基百科
http://en.wikipedia.org/wiki/Longest_common_substring_problem
http://en.wikipedia.org/wiki/Longest_common_subsequence_problem
http://en.wikibooks.org/wiki/Algorithm_implementation/Strings/Longest_common_substring
博客园
http://www.cnblogs.com/xudong-bupt/archive/2013/03/15/2959039.html
推荐:
http://blog.sina.com.cn/s/blog_54ce19050100wdvn.html
http://www.cnblogs.com/huangxincheng/archive/2012/11/11/2764625.html
http://my.oschina.net/leejun2005/blog/117167
