简介
简单的题, 直接上代码.
其实还挺复杂的.
参考链接
https://leetcode-cn.com/problems/sqrtx/solution/x-de-ping-fang-gen-by-leetcode-solution/
code
class Solution {
public:
int mySqrt(int x) {
return sqrt(x);
}
};
class Solution {
public int mySqrt(int x) {
return (int)Math.sqrt(x);
}
}
袖珍计算器法
其实是数学推导, 其实我还没怎么用过exp来进行计算和log
[sqrt{x} = x^{1/2} = (e ^ {ln x})^{1/2} = e^{frac{1}{2} ln x}
]
class Solution {
public:
int mySqrt(int x) {
if(x == 0) {
return 0;
}
int ans = exp(0.5 * log(x));
return ((long long)(ans + 1) * (ans + 1) <= x ? ans + 1 : ans);
}
};
二分查找
class Solution {
public:
int mySqrt(int x) {
int l = 0, r = x, ans = -1;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long long)mid * mid <= x) {
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return ans;
}
};
牛顿法
牛顿迭代法本质上是使用了泰勒级数的思想, 不过, 我不是特别清楚. 但是, 看了图片, 可知还是比较清晰的. 可以看参考链接
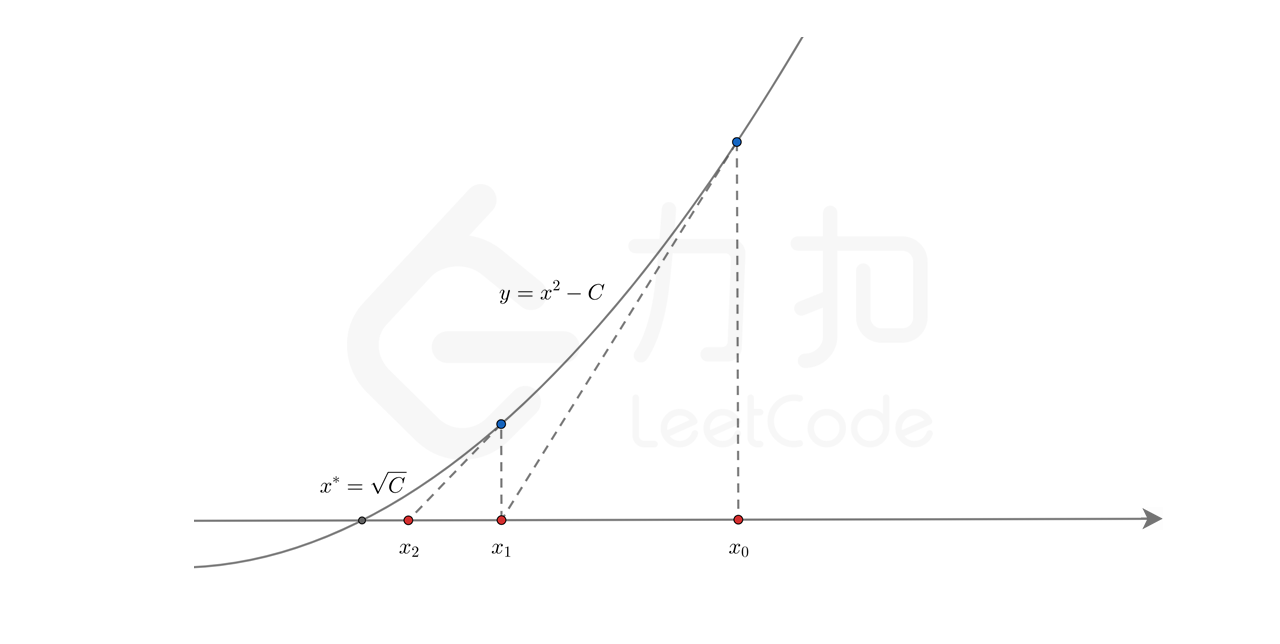
看了代码我们有了更深刻的理解
其实我们构建了一个函数
[f(x) = x^2 - C
]
其中(C)的初值设定为 输入的数 (x_0)
如果要这个方程(f(x_0) == 0) 的话, 其解 (x_{解} = sqrt{x_0})
然后我们又构建了一个直线函数求(f(x))求导后的直线与(y = 0)的交点, 当两次的点的变化很接近的时候,就是我们想要的解的范围.
class Solution {
public:
int mySqrt(int x) {
if(x == 0) {
return 0;
}
double C = x, x0 = x;
while(true){
double xi = 0.5 * (x0 + C/x0);
if(fabs(x0 - xi) < 1e-7){
break;
}
x0 = xi;
}
return int(x0);
}
};