493. Reverse Pairs

Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2*nums[j].

You need to return the number of important reverse pairs in the given array.

Example1:

Input: [1,3,2,3,1]
Output: 2

Example2:

Input: [2,4,3,5,1]
Output: 3

Note:

1. The length of the given array will not exceed 50,000.
2. All the numbers in the input array are in the range of 32-bit integer.

拿到题目后，最直观的解法就是遍历尝试所有的(i, j)组合，看看有多少种组合满足 i < j and nums[i] > 2*nums[j]这一条件。

那么，写成代码就是一个嵌套的for循环：

result := 0
for i:= 0; i < len(nums); i++ {
    for j := i; j < len(nums); j++ {
　　　　if nums[i] > nums[j]*2 {
　　　　　　result += 1
　　　　}
    }  
}

可以想见，这样解法的时间复杂度为O(n²)，空间复杂度为O(1)。

那么，有么有什么办法，可以把时间复杂度降低一些呢?

O(n*n)中，有个一个n是无法优化的，因为需要至少遍历每个元素一次，那么第二个n能否降低为＜n的值呢？

想象一下，当我们从第0个元素往右遍历的时候，随着index的增加，我们能知道哪些信息？

（想象一个卷轴打开的样子，未打开的部分是未知的，已打开的部分就能看的内容）

对于这类顺序展开的情况，我们可以将其抽象成 f(i,j) = f(i, j-1) + c的情况。其中，可以假定f(i, j-1) 已知，我们通过解决c来完成f(i, j)的求解。

那么，在这道题目中，f(i, j-1) 和 c 分别是什么呢？

假设：

f(i, j-1) 代表 [i，j-1] 范围内，满足nums[i] > 2*nums[j] 这一条件的pair数。

c 代表以 j 为end时，一共可以新增多少个pair。

故，f(i,j) 就等于 f(i, j-1)已知的pair数 +  新增第j位后新出现的pair数

那么，如何求 c 呢？

以题目的第二个例子 [2,4,3,5,1] 举例：

nums	2	4	3	5	1
index	0	1	2	3	4
c	0	0	0	0	3
result	0	0	0	0	3

只需要数一下，[0, j-1] 范围内，有多少个元素大于 2*nums[j] 即可得到c。或者换一个角度，即统计在[0, len(nums)-1] 内大于 2*nums[j] 的元素中有多少个已经出现了。

我们可以将nums数组复制一个副本并排序，得到一个sorted[]数组，并用一个bit[]数组来标记哪些元素已经出现了（0表示元素还未出现，>0表示元素出现了若干次）。

那么，问题转变成求一个范围内的累加值，即：

idx := index(sorted, 2*nums[j]+1) //查找 2*nums[j]+1这数在sorted数组中的下标

result := sum(idx, len(sorted)-1) //计算bit[]数组 [idx, n-1] 区间的累加值

求指定范围内的累加值有几种方法：

1、for 循环遍历累加，时间复杂度O(n)

func rangeSum(nums []int, start, end int) int {
　　result := 0
　　for i := start; i <= end; i++ {
　　　　result += nums[i]
　　}
　　return result
}

当数组中的值有变化时，时间复杂度仍为O(0)

2、预先先算一个累计数组，即sum[]；然后直接使用sum[j]-sum[i] 即可求得 [i, j]范围内的累加值。

var sum []int
func calcSums(nums []int)  {
　　sum = make([]int, len(nums))
　　lastSum := 0
　　for i := 0; i < len(nums); i++ {
　　　　sum[i] += nums[i] + lastSum
　　　　lastSum = sum[i]
　　}
}

func rangeSum(nums []int, start, end int) int {
　　return sum[end] - sum[start]
}

当数组不变时，预处理时间为O(n)，取值的时间为O(1)

当数组元素变化时，需要O(n)时间来更新sum数组

3、segment tree

 

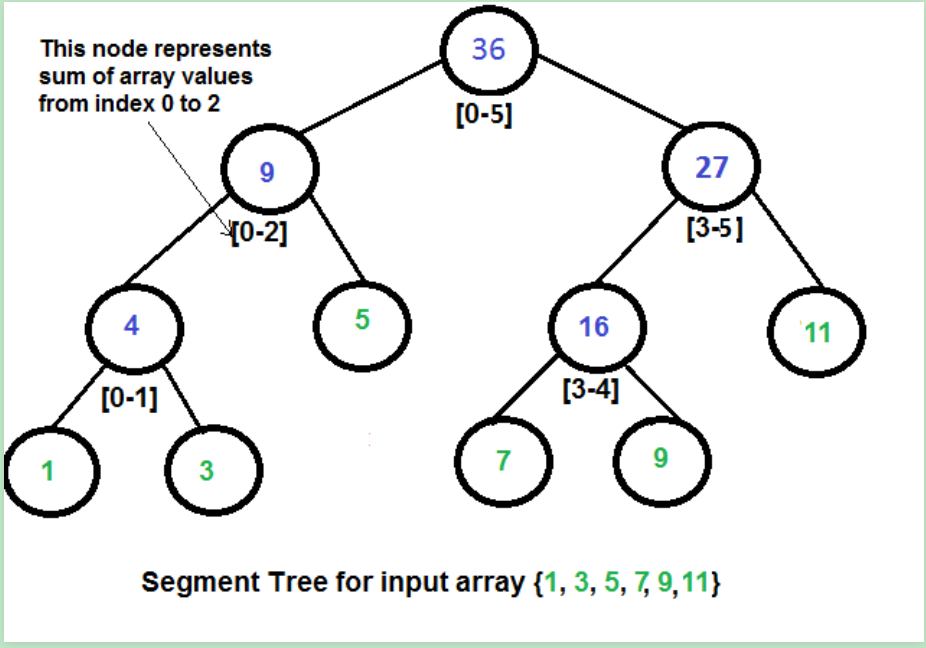
func rangeSum(nums []int, start, end int) int {
    root := addNode(nums, 0, len(nums)-1)
    getSum(root, start, end)
}

type SegmentTreeNode struct{
  sum int
  start int
  end int
  left *SegmentTreeNode
  right *SegmentTreeNode
}

func NewSegmentTreeNode(sum, start, end int, left, right *SegmentTreeNode) *SegmentTreeNode {
    return  &SegmentTreeNode{
        sum: sum,
        start: start,
        end: end,
        left: left,
        right: right,
    }
}

func addNode(nums []int, start, end int) *SegmentTreeNode {
    if start == end {
        return NewSegmentTreeNode(nums[start], start, end, nil, nil)
    }
    mid := (start+end)>>1
    left := addNode(nums, start, mid-1)
    right := addNode(nums, mid+1, end)
    return NewSegmentTreeNode(left.sum+right.sum, start, end, left, right)
}

func (node *SegmentTreeNode)update(idx, deltaVal int) {
    if node.start == idx && node.end == idx {
        node.sum += deltaValu
        return
    }

    mid := (node.start + node.end) >> 1
    sum := 0
    if idx >= mid {
        if node.right != nil {
            node.right.update(idx, deltaVal)
            sum += node.right.sum
        }
    }else{
        if node.left != nil {
            node.left.update(idx, deltaValu)
            sum += node.left.sum
        }
    }
    node.sum = sum
}

func getSum(root *SegmentTreeNode, start, end int) int {
    if root.start == start && root.end == end {
        return root.sum
    }
    //all in left subtree
    if end < root.start {
        if root.left == nil {
            return 0
        } 
        return getSum(root.left, start ,end)
    }
    //all in right subtree
    if start > root.end {
        if root.right == nil {
            return 0
        }
        return getSum(root.right, start ,end)
    }
    leftSum := getSum(root.left, start, root.start)
    rightSum := getSum(root.right, root.right, end)
    return leftSum+root.sum+rightSum
}

 segment tree的缺点是无法改变数组长度。

因为，为了保证查询时间是logn，因此在构造时使用了二分法保证树尽量平衡。

 4、fenwick tree

也称为 Binary Index Tree

 

func reversePairs(nums []int) int {
    sorted := getSortedArray(nums)
    fenwickTree := NewFenwickTree(len(nums)+1)
    result := 0
    for i := 0; i < len(nums); i++{
        if 2*nums[i]+1 <= sorted[len(sorted)-1] {
            idx := index(sorted, 2*nums[i]+1)
            count := fenwickTree.getSum(len(fenwickTree.arr)-1) - fenwickTree.getSum(idx-1)
            result += count
            fmt.Println(i, nums[i], idx, count, result, fenwickTree.arr)
        }
        //将nums[i]加入到fenwick tree中，让后面的元素可以看到它
        fenwickTree.update(index(sorted, nums[i]), 1)
    }
    return result
}

type FenwickTree struct {
    arr []int
}
func NewFenwickTree(n int) *FenwickTree {
    return &FenwickTree{arr: make([]int, n)}
}
func (ft *FenwickTree)update(idx, delta int) {
    for ;idx < len(ft.arr); {
        ft.arr[idx] += delta
        idx += idx & -idx
    }
    //fmt.Println(idx, ft.arr)
}
func (ft *FenwickTree)getSum(idx int) int {
    sum := 0
    for ;idx > 0; {
        sum += ft.arr[idx]
        idx -= idx &-idx
    }
    return sum
}

func index(sorted []int, val int) int {
    l, r, m := 0, len(sorted)-1, 0
    for ; l < r; {
        m = (l+r) >> 1
        if sorted[m] == val {
            l = m
            break
        }else if sorted[m] > val{
            r = m-1
        }else{
            l = m+1
        }
    }
    //fmt.Println(val, l+1)
    return l+1
}

func getSortedArray(nums []int) []int {
    list := make([]int, len(nums))
    for i := 0; i < len(nums); i++ {
        list[i] = nums[i]
    }
   
    sort.Slice(list, func (i,j int) bool{
        return list[i]<list[j]
    })
    return list
}

Reference:

https://leetcode.com/problems/reverse-pairs/discuss/97268/General-principles-behind-problems-similar-to-%22Reverse-Pairs%22

https://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/

https://zh.wikipedia.org/zh-hans/%E6%A0%91%E7%8A%B6%E6%95%B0%E7%BB%84

http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=3513BBA8CE0ADA3B5520B42FA344D045?doi=10.1.1.14.8917&rep=rep1&type=pdf