棋盘覆盖问题

 在一个2^k * 2^k个方格组成的棋盘中，有一个方格与其它的不同，若使用以下四种L型骨牌覆盖除这个特殊方格的其它方格，如何覆盖。

    四各L型骨牌如下图1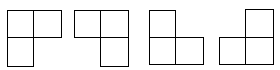



                    图1  

棋盘中的特殊方格如图2



        图2

    实现的基本原理是将2^k * 2^k的棋盘分成四块2^(k - 1) * 2^(k - 1)的子棋盘，特殊方格一定在其中的一个子棋盘中，如果特殊方格在某一个子棋盘中，继续递归处理这个子棋盘，直到这个子棋盘中只有一个方格为止如果特殊方 格不在某一个子棋盘中，将这个子棋盘中的相应的位置设为骨牌号，将这个无特殊方格的了棋盘转换为有特殊方格的子棋盘，然后再递归处理这个子棋盘。以上原理 如图3所示。



       图3

带bug版本的java实现：不知道为什么当size大于4的时候得出的是错误的结果

tr:棋盘左上角方格的行号

tc:棋盘左上角方格的列号

dr:特殊方格所在的行号

dc:特殊方格所在的列号

size:棋盘规格，size*size

public class Chessboard {
    
    public static int i=0;
    public static int size=10;
    public static int board[][] = new int[size][size];
    
    public static void chessBoard(int tr,int tc,int dr,int dc,int size){
        if(size==1) return;  //棋盘只有一个格的时候不再覆盖
        int s=size/2;         //分割棋盘 
        int t=++i;
        
        //覆盖左上角棋盘
        if(dr<tr+s&&dc<tc+s)
            //特殊方格在此棋盘中
            chessBoard(tr,tc,dr,dc,s);
        else{//此棋盘中无特殊方格
            //覆盖右下角
            board[tr+s-1][tc+s-1]=t;
            //覆盖其余方格
            chessBoard(tr,tc,tr+s-1,dc+s-1,s);
        }
        
        //覆盖右上角棋盘
        if(dr<tr+s&&dc>=tc+s)
            //特殊方格在此棋盘中
            chessBoard(tr,tc+s,dr,dc,s);
        else{//此棋盘中无特殊方格
            //覆盖左下角
            board[tr+s-1][tc+s]=t;
            //覆盖其余方格
            chessBoard(tr,tc+s,tr+s-1,tc+s,s);
        }
        
        //覆盖左下角棋盘
        if(dr>=tr+s&&dc<tc+s)
            //特殊方格在此棋盘中
            chessBoard(tr+s,tc,dr,dc,s);
        else{//此棋盘中无特殊方格
            //覆盖右上角
            board[tr+s][tc+s-1]=t;
            //覆盖其余方格
            chessBoard(tr+s,tc,tr+s,tc+s-1,s);
        }
        
        //覆盖右下角棋盘
        if(dr>=tr+s&&dc>=tc+s)
            //特殊方格在此棋盘中
            chessBoard(tr+s,tc+s,dr,dc,s);
        else{//此棋盘中无特殊方格
            //覆盖左上角
            board[tr+s][tc+s]=t;
            //覆盖其余方格
            chessBoard(tr,tc,tr+s,tc+s,s);
        }
        
    }
    
    public static void main(String[] args) {
        chessBoard(0, 0, 2, 2, 4);
        for(int i=0;i<4;i++)
            for(int j=0;j<4;j++)
            {
                if(j==0)
                    System.out.println();
                System.out.print(" "+board[i][j]);
            }
    }

}

没法保证chessBoard函数中无特殊方格的子棋盘被正确覆盖。