线性代数-矩阵的运算

1、矩阵的加减法

定义

A = (a_ij)mxn 、B = (b_ij)mxn；是两个同型矩阵（行数和列数分别相等），则矩阵A、B和定义为：

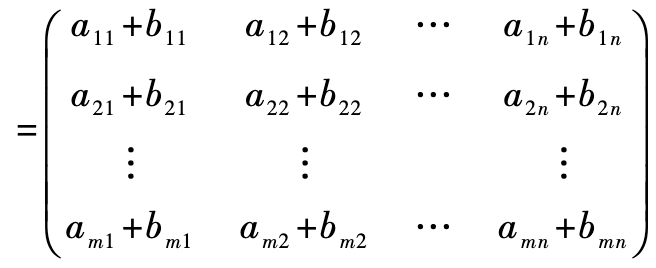
 只有同型矩阵才能进行加法计算

运算定律

• 交换律：A + B = B + A
• 结合律：（A + B）+ C = A + (B + C)
• A + O = A = O + A （O为零矩阵）
• A + （-A） = O （矩阵减法的定义）

设：

 则：

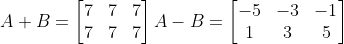
2、矩阵的数乘

定义

数k与矩阵A乘法定义为：

 记作：kA = (ka_ij)_mxn;

矩阵的加法和数乘运算，称为矩阵的线性运算。

运算定律

• 结合律：(kl)A = k(lA)
• 分配律：k(A+B) = kA + kB;(k + l)A = kA + lA;
• 1A = A;0A = O

 3、乘法运算

定义

设A = (aij)mxs、B=(bij)sxn AB的乘发定义为

 注意：只有当A矩阵的列数等于B矩阵的行数，矩阵乘积AB才有意义；且乘积C矩阵的行数等于A矩阵的行数、C矩阵的列数等于B矩阵的列数。

如：A是(2x3)矩阵,B是(3x4)矩阵，则AB为(2x4)矩阵，BA无意义。

运算定律

• 矩阵乘法不满足交换律：一般AB不等于BA，如果AB = BA，即记作A、B可交换
• AB = 0 未必 A = O或者 B = O
• 不满足消除律，即AB = AC 未必B = C

矩阵乘法满足下面运算律：

• 结合律：(AB)C = A(BC)
• 左分配律：A(B+C) = AB+AC
• 右分配律：(B+C)A = BA+CA
•  k(AB) = (kA)B = A(kB)
• 设A为mxs矩阵，则 I_mA = A ，AI_s = A（I为单位矩阵）
• AO=O OA=O
• A^kA^{l =} A^k+l  (A^k)^l = A^kl (kl皆为非负整数)

矩阵乘法中，单位矩阵与零矩阵，有类似于数字乘法1，0的作用。

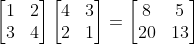
4、矩阵的转置

定义

mxn的矩阵A，行列交换后得到nxm的矩阵，称为A的转置矩阵，记作A'。

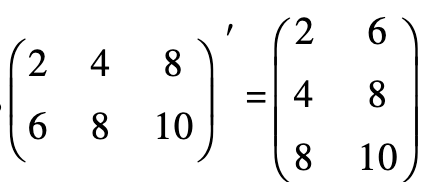
运算定律

• (A')' = A
• (A+B)' = A' + B'
• (kA') = kA'
• (AB)' = B'A'

若A' = A则称A为对称矩阵；显然A为方阵。对称矩阵主对角线对称位置的元素分别相等。

 若A' = -A 则称A为反对称矩阵，反对称矩阵必为方阵。且对角线上的元素全为0。