聚类算法之DBSCAN

DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。

该算法将具有足够密度的区域划分为簇，并在具有噪声的空间数据库中发现任意形状的簇，它将簇定义为密度相连的点的最大集合。

•  可以在有噪音的数据中发现各种形状和各种大小的簇。
• 寻找被低密度区域分离的高密度区域，这些高密度区域就是一个一个的簇，这里的密度指的是一个样本点的领域半径内包含的点的数目
• 可以用来过滤噪声孤立点数据，发现任意形状的簇（因为它将簇定义为密度相连的点的最大集合）
• 与k-means算法的不同之处在于它不需要事先指定划分的簇的数目。
  
  

基础概念

    作为最经典的密度聚类算法，DBSCAN使用一组关于“邻域”概念的参数来描述样本分布的紧密程度，将具有足够密度的区域划分成簇，且能在有噪声的条件下发现任意形状的簇。在学习具体算法前，我们先定义几个相关的概念：

• 邻域：对于任意给定样本x和距离ε，x的ε邻域是指到x距离不超过ε的样本的集合；

• 核心对象：若样本x的ε邻域内至少包含minPts个样本，则x是一个核心对象；

• 密度直达：若样本b在a的ε邻域内，且a是核心对象，则称样本b由样本x密度直达；

• 密度可达：对于样本a，b，如果存在样例p1,p2,...,pn,其中，p1=a,pn=b,且序列中每一个样本都与它的前一个样本密度直达，则称样本a与b密度可达；

• 密度相连：对于样本a和b，若存在样本k使得a与k密度可达，且k与b密度可达，则a与b密度相连。

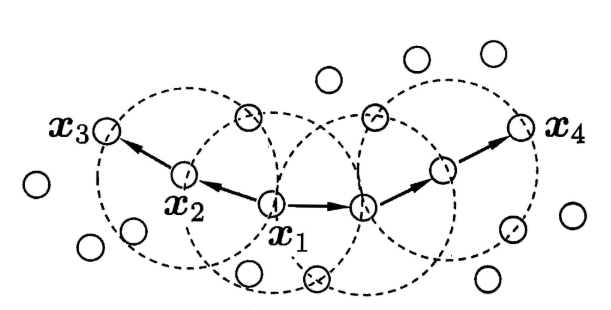
当minPts=3时，虚线圈表示ε邻域，则从图中我们可以观察到：

• x1是核心对象；

• x2由x1密度直达；

• x3由x1密度可达；

• x3与x4密度相连。

为什么要定义这些看上去差不多又容易把人绕晕的概念呢？其实ε邻域使用（ε，minpts）这两个关键的参数来描述邻域样本分布的紧密程度，规定了在一定邻域阈值内样本的个数（这不就是密度嘛）。那有了这些概念，如何根据密度进行聚类呢？

DBSCAN聚类的原理很简单：由密度可达关系导出最大密度相连的样本集合（聚类）。这样的一个集合中有一个或多个核心对象，如果只有一个核心对象，则簇中其他非核心对象都在这个核心对象的ε邻域内；如果是多个核心对象，那么任意一个核心对象的ε邻域内一定包含另一个核心对象（否则无法密度可达）。这些核心对象以及包含在它ε邻域内的所有样本构成一个类。

　　那么，如何找到这样一个样本集合呢？一开始任意选择一个没有被标记的核心对象，找到它的所有密度可达对象，即一个簇，这些核心对象以及它们ε邻域内的点被标记为同一个类；然后再找一个未标记过的核心对象，重复上边的步骤，直到所有核心对象都被标记为止。

　　算法的思想很简单，但是我们必须考虑一些细节问题才能产出一个好的聚类结果：

• 首先对于一些不存在任何核心对象邻域内的点，再DBSCAN中我们将其标记为离群点（异常）；
• 第二个是距离度量，如欧式距离，在我们要确定ε邻域内的点时，必须要计算样本点到所有点之间的距离，对于样本数较少的场景，还可以应付，如果数据量特别大，一般采用KD树或者球树来快速搜索最近邻，不熟悉这两种方法的同学可以找相关文献看看，这里不再赘述；
• 第三个问题是如果存在样本到两个核心对象的距离都小于ε，但这两个核心对象不属于同一个类，那么该样本属于哪一个类呢？一般DBSCAN采用先来后到的方法，样本将被标记成先聚成的类。

之前我们学过了kmeans算法，用户需要给出聚类的个数k，然而我们往往对k的大小无法确定。DBSCAN算法最大的优势就是无需给定聚类个数k，且能够发现任意形状的聚类，且在聚类过程中能自动识别出离群点。那么，我们在什么时候使用DBSCAN算法来聚类呢？一般来说，如果数据集比较稠密且形状非凸，用密度聚类的方法效果要好一些。

DBSCAN算法优点：

1. 不需要事先指定聚类个数，且可以发现任意形状的聚类；

2. 对异常点不敏感，在聚类过程中能自动识别出异常点；

3. 聚类结果不依赖于节点的遍历顺序；

DBSCAN缺点：

1. 对于密度不均匀，聚类间分布差异大的数据集，聚类质量变差；

2. 样本集较大时，算法收敛时间较长；

3. 调参较复杂，要同时考虑两个参数；

代码实现：

#用Python实现DBSCAN聚类算法
#导入数据：
import pandas as pd
from sklearn.datasets import load_iris
# 导入数据,sklearn自带鸢尾花数据集
iris = load_iris().data
print(iris)

#使用DBSCAN算法：
from sklearn.cluster import DBSCAN

iris_db = DBSCAN(eps=0.6,min_samples=4).fit_predict(iris)
# 设置半径为0.6，最小样本量为2，建模
db = DBSCAN(eps=10, min_samples=2).fit(iris)
 
# 统计每一类的数量
counts = pd.value_counts(iris_db,sort=True)
print(counts)

#可视化：
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = [u'Microsoft YaHei']

fig,ax = plt.subplots(1,2,figsize=(12,12))

# 画聚类后的结果
ax1 = ax[0]
ax1.scatter(x=iris[:,0],y=iris[:,1],s=250,c=iris_db)
ax1.set_title('DBSCAN聚类结果',fontsize=20)

# 画真实数据结果
ax2 = ax[1]
ax2.scatter(x=iris[:,0],y=iris[:,1],s=250,c=load_iris().target)
ax2.set_title('真实分类',fontsize=20)
plt.show()

#这时候可以使用轮廓系数来判定结果好坏，聚类结果的轮廓系数，定义为S，是该聚类是否合理、有效的度量。
#聚类结果的轮廓系数的取值在[-1,1]之间，值越大，说明同类样本相距约近，不同样本相距越远，则聚类效果越好。
from sklearn import metrics  
# 就是下面这个函数可以计算轮廓系数（sklearn真是一个强大的包）
score = metrics.silhouette_score(iris,iris_db) 
score

参考资料

1、https://mp.weixin.qq.com/s/heRnd6lA4H1Cj7S4wR0SkQ

2、DBSCAN密度聚类算法 - 刘建平Pinard - 博客园 (cnblogs.com)

3、https://zhuanlan.zhihu.com/p/185623849

4、https://blog.csdn.net/wuxintdrh/article/details/105449771

5、https://www.cnblogs.com/pinard/p/6217852.html

---------------------------本博客所有内容以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，并且是非商业用途，谢谢！---------------------

作者：enhaofrank

出处：https://www.cnblogs.com/enhaofrank/

中科院硕士毕业

现为深漂打工人