Link-Cut Tree的基本思路是用splay的森林维护一条条树链。
splay的森林,顾名思义,就是若干splay组成的东西。
每个splay都有一个根节点,所以lct里的splay不能记录根节点,因为根节点有好多。
我们开一个bool数组记录每个点是否为根节点。
每个splay都维护一条重链,重链之间的轻链在splay里只从儿子指向父亲,而父亲并没有这个儿子。
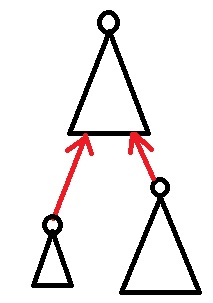
就像图里的红箭头。
每个splay都表示一条重链,这个splay的中序遍历与链上节点的深度顺序是一致的。
接下来是splay里最重要的操作:access(p)
就是指打通从p到整棵树的树根的一条重链。
同时也把p下面接的链变成轻链。
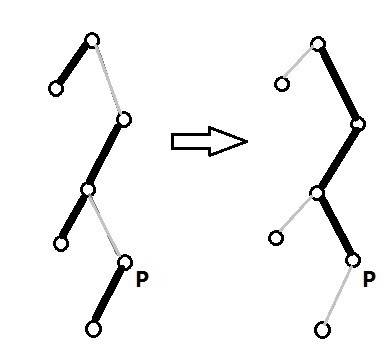
之后还有一个操作:move_to_root,把p变成整棵树的根。
在access之后,p和树根之间是重链直接连接,而一个splay维护一个重链,所以此时p和根已经在一个splay里了。
我们只需要splay(p)即可。
但是这样的话破坏了深度的性质。
把左右反转一下就行了:reverse(p)
接下来就是link和cut的操作。
link(x,y)很简单,mtr(x),之后接一条从x到y的轻链即可。
cut(x,y)的话,mtr(x),access(y),splay(y),x就是y的左儿子了。删掉父子关系即可。
查询连通性:mtr(x),access(y),splay(y),x就在y的子树里了。x=f[x]一直往上跳,判断最后y的终点是不是x。
这些大概是最最基础的操作了,子树信息什么的都不用维护。
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define id(x) (s[f[x]][1]==x) 5 using namespace std; 6 7 int n,m; 8 int f[10005],s[10005][2]; 9 bool rev[10005],rt[10005]; 10 11 void reverse(int p) 12 { 13 swap(s[p][0],s[p][1]); 14 rev[p]^=1; 15 } 16 17 void pushdown(int p) 18 { 19 if(!rev[p])return; 20 reverse(s[p][0]); 21 reverse(s[p][1]); 22 rev[p]=0; 23 } 24 25 void down(int p) 26 { 27 if(!rt[p])down(f[p]); 28 pushdown(p); 29 } 30 31 void rotate(int p) 32 { 33 int k=id(p); 34 int fa=f[p]; 35 if(rt[fa])rt[p]=1,rt[fa]=0; 36 else s[f[fa]][id(fa)]=p; 37 s[fa][k]=s[p][!k]; 38 s[p][!k]=fa; 39 f[p]=f[fa]; 40 f[fa]=p; 41 f[s[fa][k]]=fa; 42 } 43 44 void splay(int p) 45 { 46 down(p); 47 while(!rt[p]) 48 { 49 int fa=f[p]; 50 if(rt[fa]) 51 { 52 rotate(p); 53 return; 54 } 55 if(id(p)^id(fa))rotate(p); 56 else rotate(fa); 57 rotate(p); 58 } 59 } 60 61 void access(int p) 62 { 63 int son=0; 64 while(p) 65 { 66 splay(p); 67 rt[s[p][1]]=1,rt[son]=0; 68 s[p][1]=son; 69 son=p,p=f[p]; 70 } 71 } 72 73 void mtr(int p) 74 { 75 access(p); 76 splay(p); 77 reverse(p); 78 } 79 80 void link(int x,int y) 81 { 82 mtr(x); 83 f[x]=y; 84 } 85 86 void cut(int x,int y) 87 { 88 mtr(x); 89 access(y); 90 splay(y); 91 s[y][0]=f[x]=0; 92 rt[x]=1; 93 } 94 95 void check(int x,int y) 96 { 97 mtr(x); 98 access(y); 99 splay(y); 100 while(!rt[x])x=f[x]; 101 printf("%s ",(x==y?"Yes":"No")); 102 } 103 104 int main() 105 { 106 scanf("%d%d",&n,&m); 107 for(int i=1;i<=n;i++)rt[i]=1; 108 char op[15]; 109 int x,y; 110 while(m--) 111 { 112 scanf("%s",op+1); 113 scanf("%d%d",&x,&y); 114 if(op[1]=='C')link(x,y); 115 if(op[1]=='D')cut(x,y); 116 if(op[1]=='Q')check(x,y); 117 } 118 return 0; 119 }