第二章 分治算法
1. 分治算法的原理
分治法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
分治法所能解决的问题一般具有以下几个特征(这部分参考了这篇博文http://blog.csdn.net/com_stu_zhang/article/details/7233761)：
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解；
4) 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。
第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。
第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。
分治法的分析过程：
即总共的复杂度=划分为多个子问题的复杂度+求解各个子问题的复杂度+合并子问题的复杂度，用这个便可以建立递归方程，再利用上一章和的估计与界限中的第三种方法：递归方程 便可以得到时间复杂度了，当然也可以套用主定理。
2. 使用分治法解决的一些经典问题
(1)归并排序
归并排序的分治策略是将整个n个数分为左边，右边各一半，每个部分归并排序的时间复杂度为T(n/2),总共有两部分，所以求解子问题的复杂是2T(n/2)。划分子问题不需要什么多余的操作计算，直接取左右部即可，所以忽略不计。至于合并子问题操作，是将左部排好序的n/2个数和右部排好序的n/2个数合并成一个有序的数组，归并排序的合并步是比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可，可以看出合并有序数列的效率是比较高的，可以达到O(n)。所以整个归并排序的时间复杂度T(n)=2T(n/2)+O(n),有了递归方程，套用主定理:
这里的的f(n)的阶是O(n), a=2, b=2, 
是n，所以
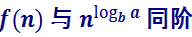，则立即推出归并排序的时间复杂度是：Θ (nlogn) ，不过这里我有个疑问就是：按照主定理结果是Θ (nlogn)，但是我网上搜了下归并排序的时间复杂度结果都是O(nlogn)，归并排序的最好、最坏和平均时间复杂度都是O(nlogn)，不过我看一般的书算时间复杂度是只用到了 O 记号，Ω 和 Θ 几乎没用过。。。。。 还有就是上一章讲到复杂函数的阶的时候，ppt把T(n)=Θ(f(n)) 定义为 “给出了算法时间复杂度的上界和下界”，意思就是如果T(n)=Θ(f(n)) 那就可以推出T(n)=O(f(n))和T(n)=Ω(f(n))？。。。。。是这样的么？拿不准啊。。。希望有大佬帮我答疑解惑下，感激不尽。
2017/1/6 今天看了算法导论，明白了这个问题，根据第28页的定理3.1: 对任意两个函数f(n)和g(n), 我们有f(n)=Θ(g(n)), 当且仅当f(n)=O(g(n))且f(n)=Ω(g(n)). 验证了我的想法
(2)找最大值
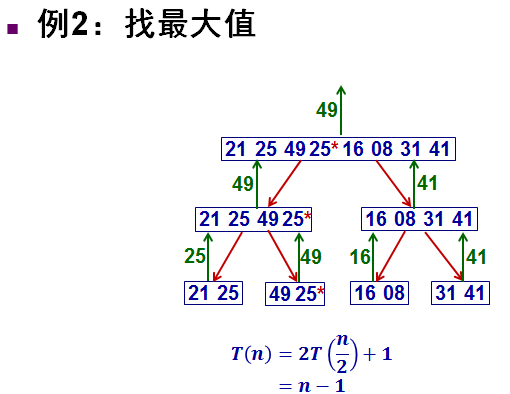
为什么总比较次数是n-1呢？很简单，上面是个二叉树结构，每个数节点会比较一次，比较次数是树的节点数，最下层应该有 n/2 个叶节点，对于二叉树来说，叶子节点数=度为2的节点数+1，所以推出度为2的节点的数量是 n/2-1, 所以上面的整个树共有n/2+n/2-1=n-1个节点, 即共有n-1次大小的比较。
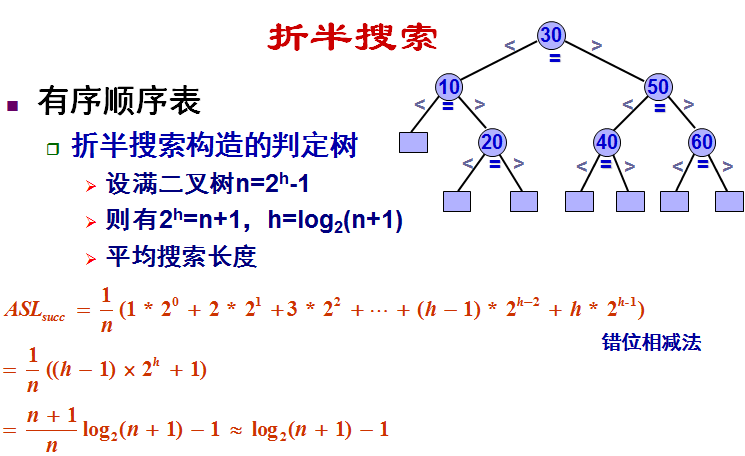
(3)折半搜索
(4)大整数乘法
其中需要理解的是这个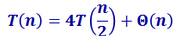
是怎么来的，AC，AD，BC，BD这四象都是n/2位数乘n/2位数，所以总共的复杂度是4T(n/2)，AD+BC 二进制整数和二进制整数想加，一位一位的加，故复杂度是Θ(n)。
(5)矩阵乘法
n/2*n/2的矩阵共有n/2*n/2=n2/4个元素，那么矩阵之间的加减操作的复杂度便是Θ(n2)
(6)快速排序
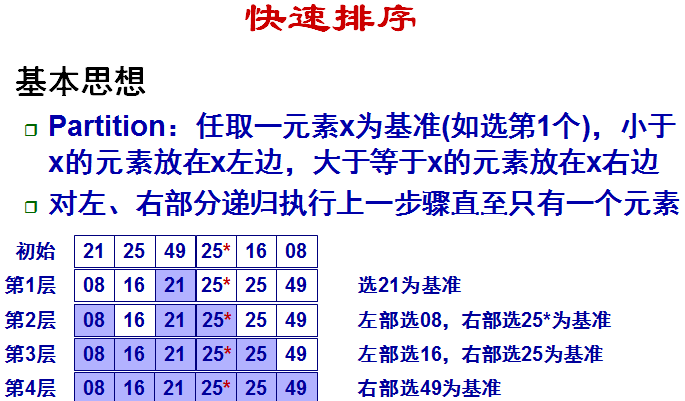
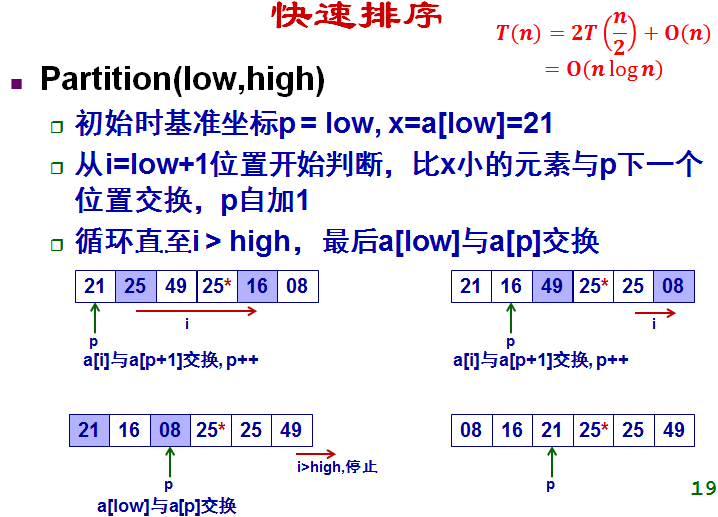
(7)求第k小元素
怎么理解这个呢？画一副图就知道了：
一列表示一组5个数，取中间的一组数，再取这组数的第M/2小的元素m，图上画的把中间这组数排好序了，那么大于m的数至少有图中圈的那么多，因为最后一组可能不足3个，以及m所在的那组下面只有两个(m不能算在内了),所以这里排除了最后一列和中间那一列。那么我们继续：
即求第k小元素总的时间复杂度 = 将整个数组划分为n/5(向上取整)并每组排序的时间复杂度O(n)+从每组第3个元素构成的数组M中寻找m的时间复杂度T(n/5)+Conquer的时间复杂度T((7n/10)+6)
(8)堆排序
这个理解起来比较容易，pass掉，记住时间复杂度是O(nlogn)
(9)最近点对
在二维平面上的n个点中找距离最近的两个点，输入是一系列的点，输出距离最近的两个点
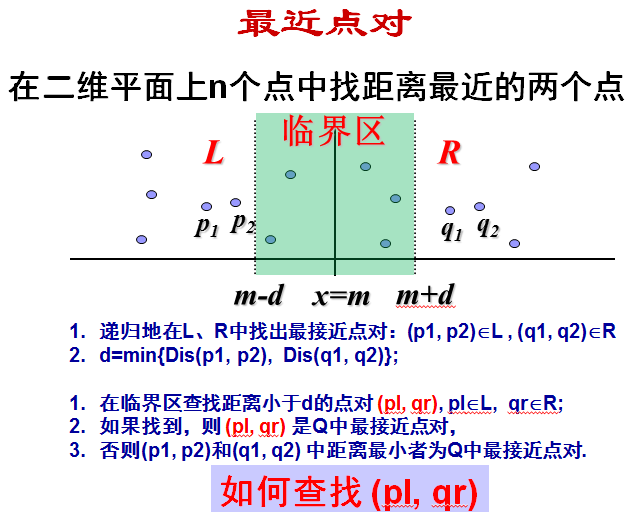
好难理解。。。。。。，难点是在于如何理解在临界区查找距离小于d的点对这块，烦烦烦。还是一步步来分析吧:
思考路径：将所有的点按照x坐标值和y坐标值排序——>按照x轴分成大小相等的两个子集合——>递归地找这两个子集合中的最近点对，设为d
现在问题就是：最近点对有可能是横跨左右两个集合的，在左集合和右集合各取一点所得到的点对，其中最小的距离能够小于d的话，那么这个点对便是整个点集合的最近点对了。所以现在按照x轴的中间线往左往右各推d距离(任何一边不可能大于d，否则大于d的那部分的点到右集合的距离肯定是大于d的)。
现在有一个理解的关键点：如果在左部任取一点pl，假设在右部能找到和它距离小于d的点qr，那么应该满足两个条件:
1. pl和qr的距离小于d 2. 因为d是左右两部分的最近点对的距离，所以右部任何两个点的距离都不可能小于d，即qr和它所在的那个区间的所有点的距离都不小于d
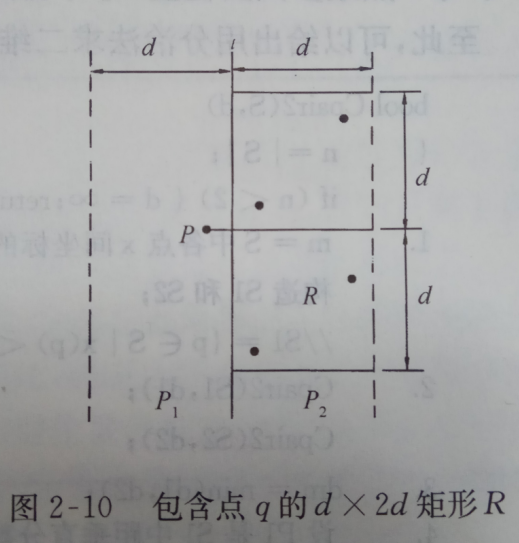
由上述可以推出对于左部的点pl，满足上述两个条件的的点在右部最多只有6个。现在来解释这个：对于左部的任意一点pl，与它构成距离小于d的右部的点一定是落在矩形R中(p为圆心，d为半径作圆，再取极端情况pl落在中位分割线上即可得此结论)。将矩形R的长为2d的边3等分，长为d的边2等分), 由此导出6个(d/2)x(2d/3)的矩形：
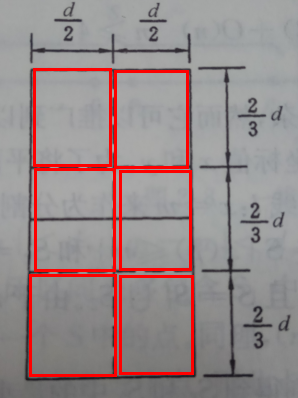
现在利用鸽舍原理，原理1： 把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。假设矩形R中有多于6个点，那么6个矩形中至少有一个有2个以上的点，假设u，v是位于同一小矩形中的的2个点，则
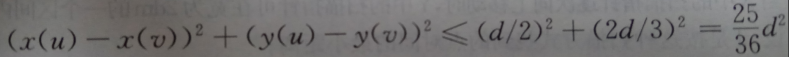
即distance(u,v)<=5d/6<d. 这与d的意义相矛盾，由此反证推出矩形R中最多只能有6个点。解决了这个，现在的问题是如何找这6个点呢？将左部的点pl和右部所有的点投影到垂线上(中位分割线)
上，由于能与点pl一起构距离小于d的点一定在矩形R中，所以他们在上的投影点距pl在上投影点的距离小于d。由上面的分析可知这种投影点最多只有6个，因此，若将左部和右部中所有的点按照其y坐标排好序，对左部中的所有点，对排好序的点列做一次扫描，就可以找出所有最近点对的候选者。对左部中的每一点最多只要检查右部中排好序的相继6个点。
分治法求最近点对的时间复杂度：
(10)快速傅立叶变换
ppt这块完全看不明白。。。。。。汗啊。。。。 上课不认真听的后果ToT。时间复杂度是nlogn
(11)寻找凸包
找到最下最左顶点，其他顶点与它连线，按夹角从小到大排序，夹角最小的开始寻找凸包点。
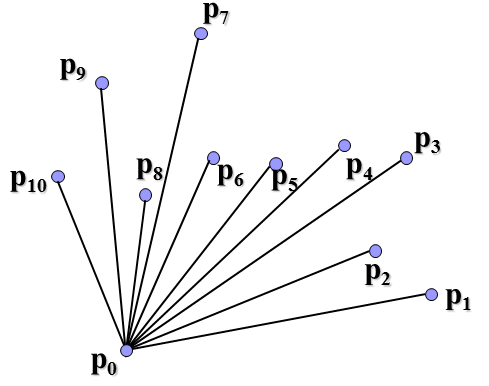
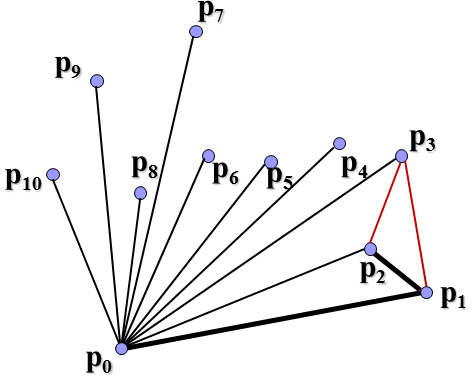
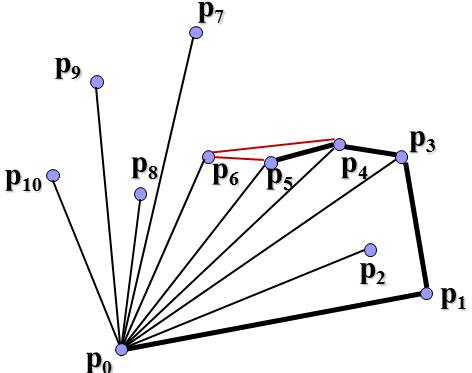
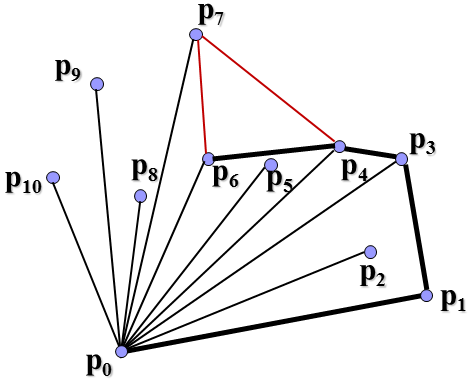
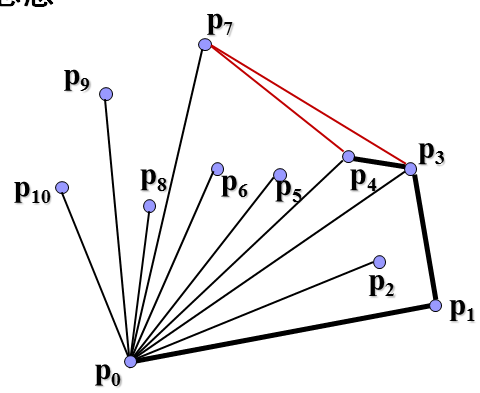
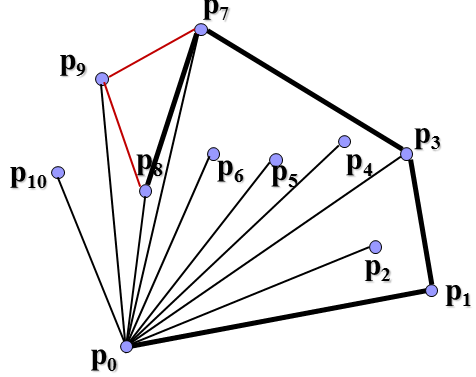
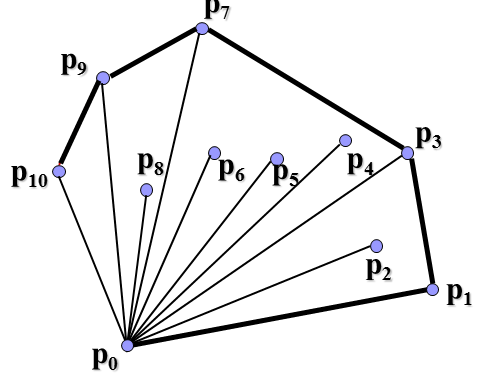
可以看到这里连线是有讲究的，如果与与下一顶点的连线在上一连线的右侧(如p2到p3)，那么就删除和下一顶点的连线上一连线，将上一点(如p1)直接和下一点连接起来，再作如此判断。这就是Graham-scan的基本思想。总的时间复杂度是O(nlogn)。现在怎么利用分治法来解决寻找凸包问题呢？
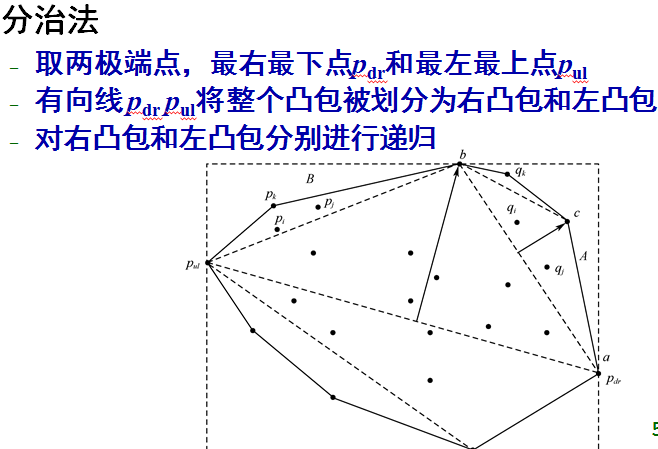
分治法寻找凸包的平均时间复杂度是O(nlogn)，最坏情况是O(n2)。注意这里递归划分自区间，每次找的是距离划分直线最远的点。
3. 平衡的概念
关于小节的总结就是：在使用分治法和递归时要尽量把问题分成规模相等，或至少是规模相近的子问题，即平衡。