https://loj.ac/problem/10016
题目描述
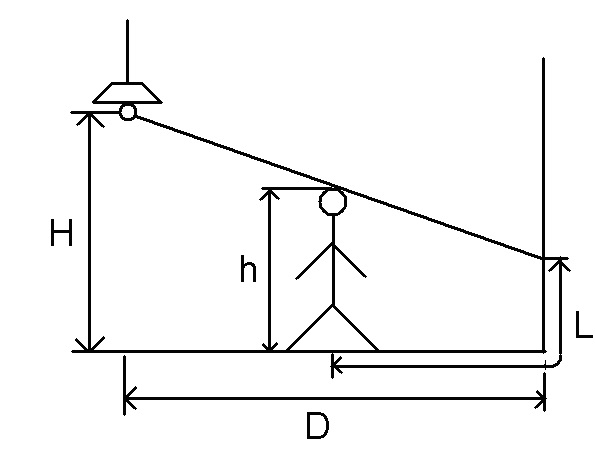
已知(H、h、D),求最大影子长度(L)。
思路

这道题是纯粹的数学题,只是用三分来求解最值而已。我们将灯的光线和地板延长交于一点,那么可以形成一组相似三角形。我们设人到灯的距离为(x),人到墙的距离为(x1),人的影子的高度为(x2),那么根据相似和三角函数可知:
[x1 = D - x \
连线交点的角:tanθ = (H - h)/ x \
那么可以知道:x2 = H - tanθ * D = H - D *(H - h) / x \
由此可得 L = x1 + x2 = D - x + H - D*(H - h)/ x
]
而数学好的同志会知道这是一个打钩函数,并且在([ 0 , +∞ ]) 为单峰函数,那么就可以用三分求最值时(x)的值。不过纯数学也是可以解决的,可以直接求出最值时(x)的取值,我在此就不加叙述了。
代码
#include <bits/stdc++.h>
using namespace std;
double H,h,D;
double f(double x)
{
double x1=D-x;
double x2=H-(H-h)*D/x;
return x1+x2;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%lf%lf%lf",&H,&h,&D);
double l=(H-h)*D/H,r=D,eps=1e-8;
while(r-l>eps)
{
double lmid=l+(r-l)/3;
double rmid=r-(r-l)/3;
if(f(lmid)<=f(rmid))l=lmid;
else r=rmid;
}
printf("%.3lf
",f(r));
}
return 0;
}