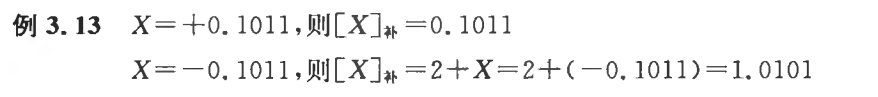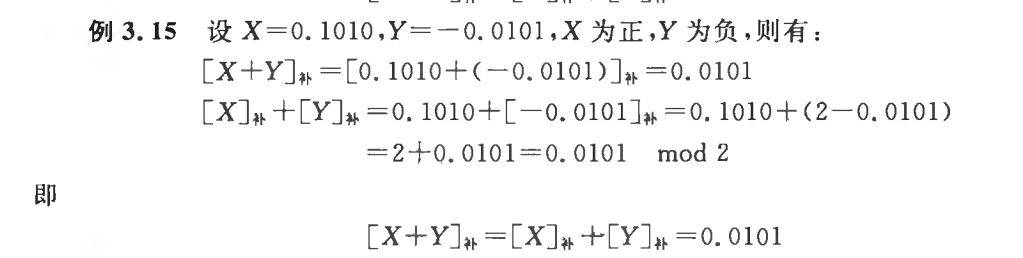运算方法和运算部件
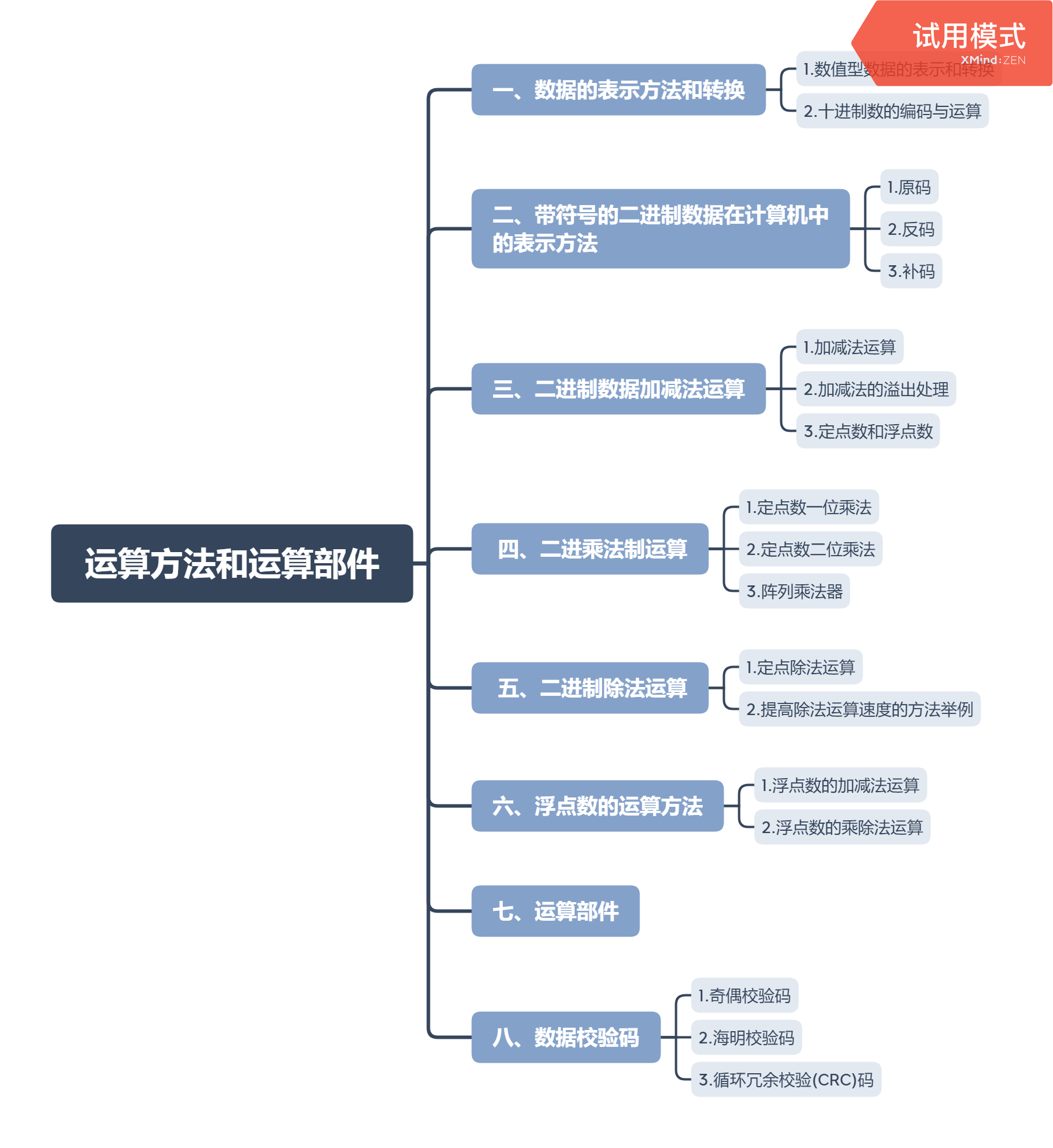
一、数据的表示方法和转换
1.数值型数据的表示和转换
-
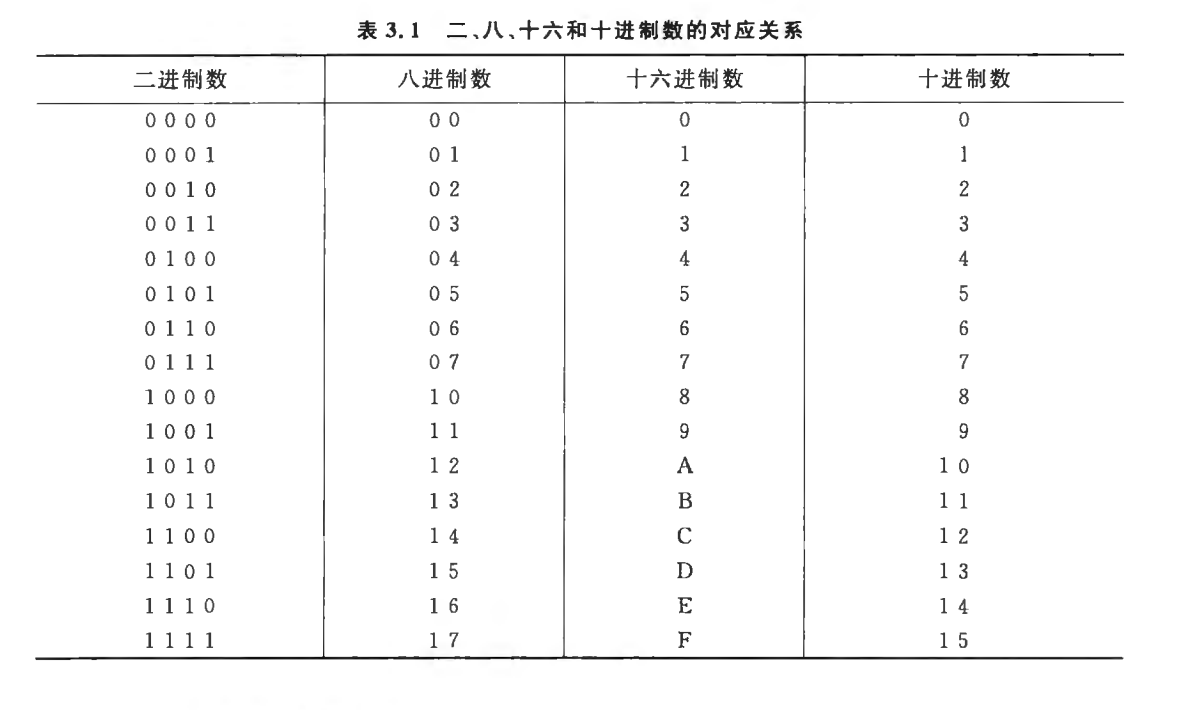
数制表示:
-
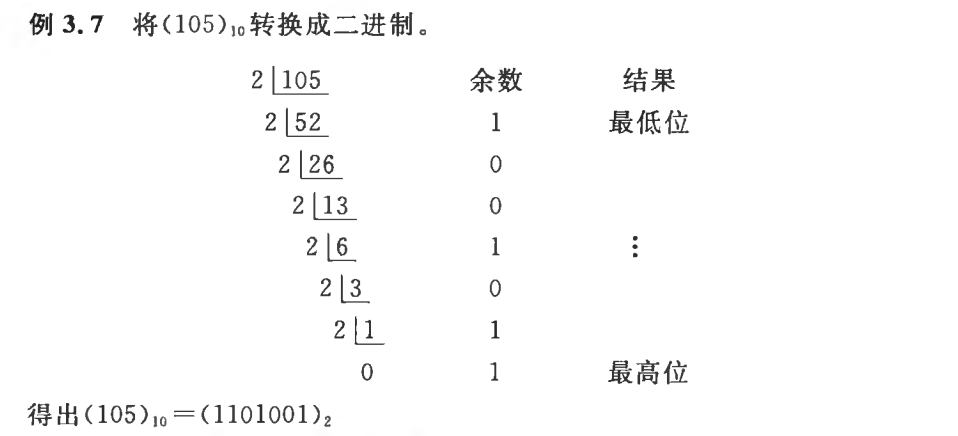
数制转换:
-
数据符号的表示:
- 在计算机中正负号需要数字化,一般用0表示正号,1表示负号,正号有时可省略
2.十进制数的编码与运算
-
有权码:
- 定义:表示一位十进制数的二进制码的每一位有确定的权
- 一般使用8421码(BCD码)

-
无权码:
- 定义:表示一个十进制数位的二进制码的每一位没有确定的权
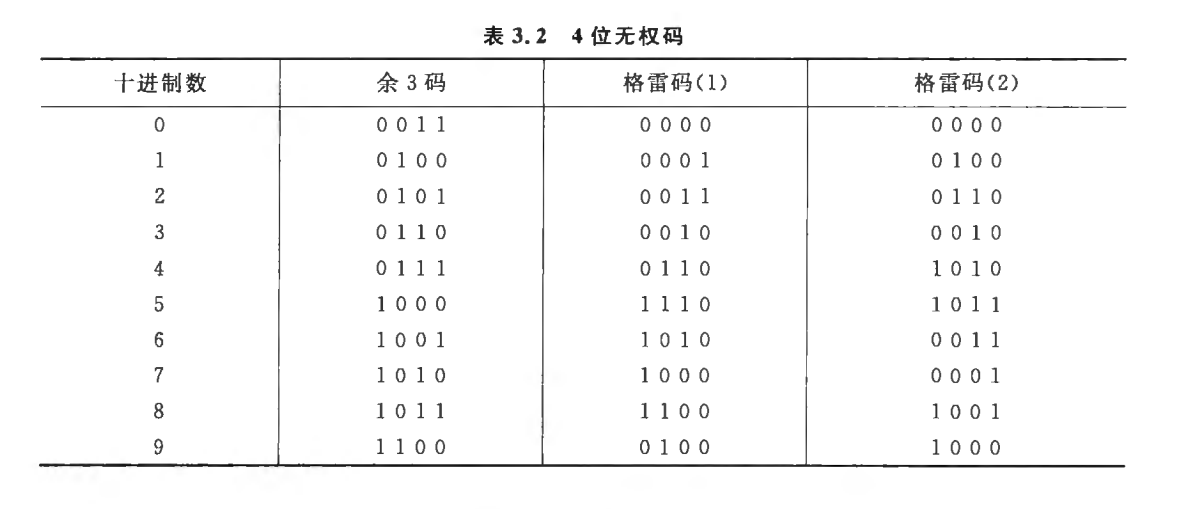
- 余3码:8421码的基础上,每个编码加上0011
- 加法修正:不产生进位时减3;产生进位时加3

- 格雷码:相邻编码只有1位不同,其余3位相同
- 一个编码变到另一个只有1位发生变化,构成计数器
二、带符号的二进制数据的表示方法
机器数:在计算机中表示的带符号的二进制数
- 表示方式:原码、反码、补码
- 先假设机器数为小数,符号位在最左面,小数点在符号位和数值之间,数的真值用X表示
1.原码
- 定义:机器数的最高位为符号位,0表示正数,1表示负数,数值位跟随其后,并以绝对值形式给出

- 例:

- 特点:

2.反码
- 定义:

- 例:
- 特点:

3.补码
-
定义:

-
例:
-
特点:

4.移码
- 定义:

- 例:

- 特点:

5.各码之间的转换
- 仿照原码转换成补码或反码的过程再重复执行一遍,即可还原成原码形式
- 例:
三、二进制数据加减法运算
1.加减法运算
- 逻辑示例:

2.加减法的溢出处理
- 法一:
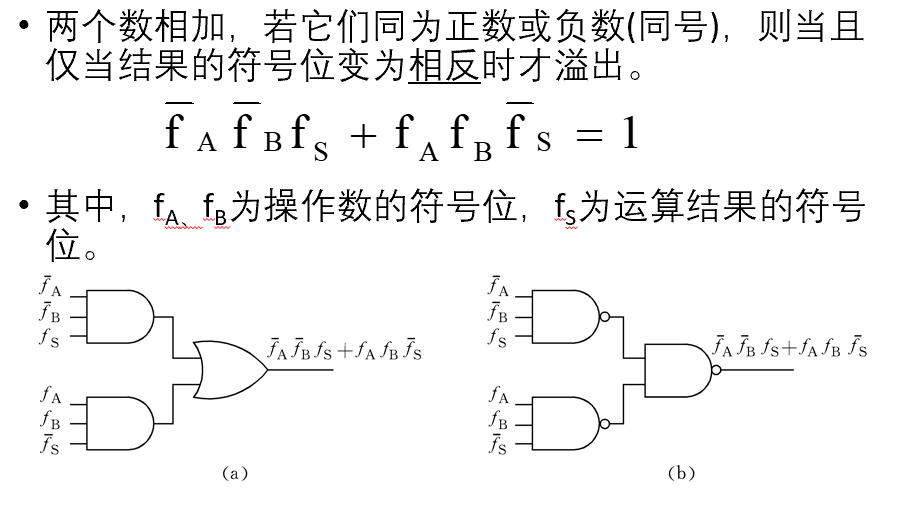
- 法二:
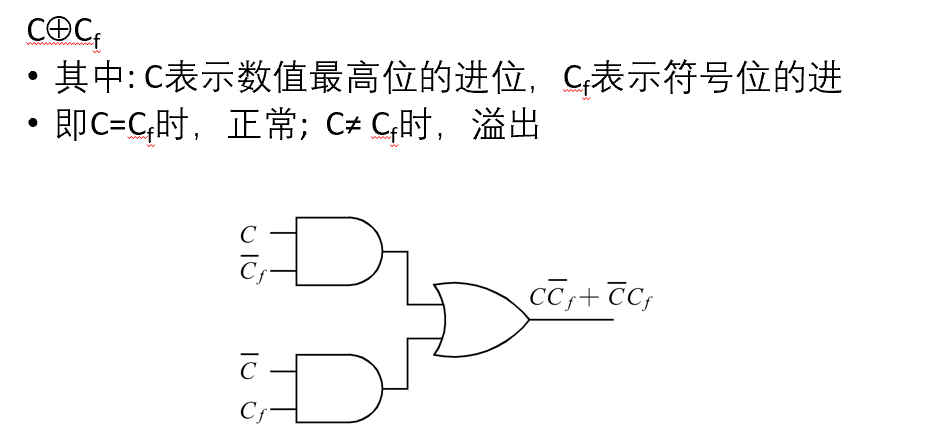
- 法三:

3.定点数和浮点数
- 定点数:指小数点固定在某个位置上的数据
- 浮点数:指小数点位置可浮动的数据

- 表示:
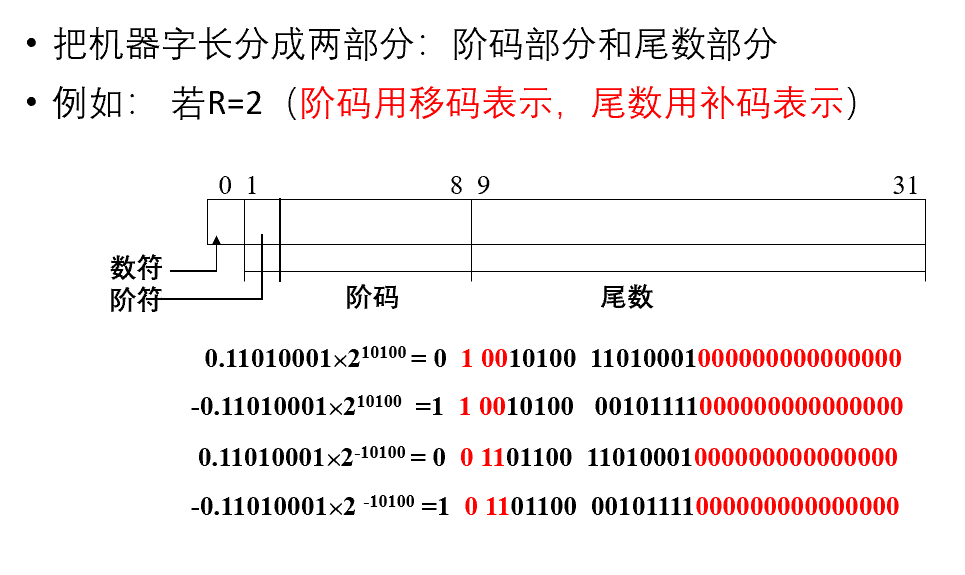
- 规格化:

- IEEE 754国际标准:
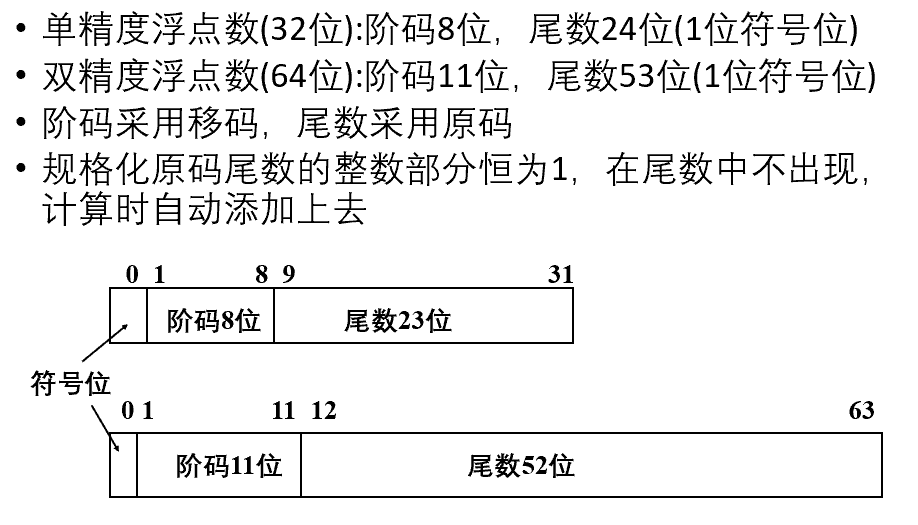
- 表示:
4.计算机中数据数值范围和精度
四、二进乘法制运算
1.定点数一位乘法
-
定点原码一位乘法:
- 规则:

- 例:
- 人工计算:



- 人工计算:
- 规则:
-
定点补码一位乘法:
- 规则:


- 例:

- 规则:
2.定点原码二位乘法
- 规则:


- 例:
 如果最后一次操作欠下+4X,则最后一次右移2位后还需补充+X操作,+X后不再移位
如果最后一次操作欠下+4X,则最后一次右移2位后还需补充+X操作,+X后不再移位
3.阵列乘法器
- 特点:内部结构规则性强,适于用超大规模集成电路实现
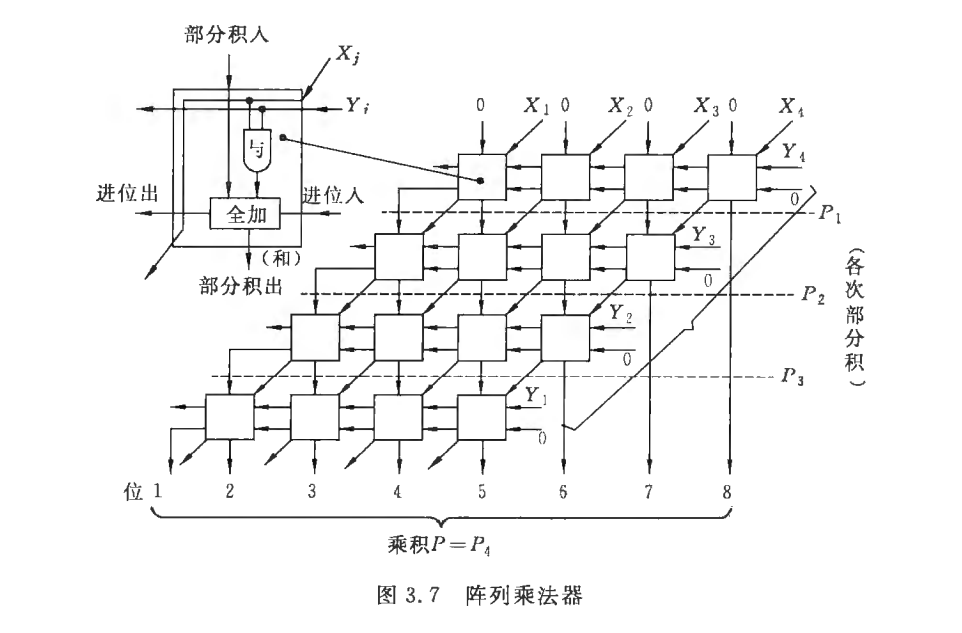
五、二进制除法运算
1.定点除法运算
- 特点:

- 恢复余数法:
- 规则:

- 特点:当某一次减Y的差值为负时,要多一次加Y恢复余数的操作,在计算机很少采用
- 规则:
- 加减交替法:
- 规则:

- 特点:不恢复余数的除法方案
- 例:

- 规则:
2.提高除法运算速度的方法举例
-
跳0跳1除法:
- 规则:

- 例:

- 规则:
-
通过乘法操作实现:
- 规则:

- 例:

- 规则:
六、浮点数的运算方法
1.浮点数的加减法运算
-
规则:
-
流程图:

-
流程:


-
-
例:

2.浮点数的乘除法运算
- 规则:


- 例:
- 特点:

3.浮点数的除法运算
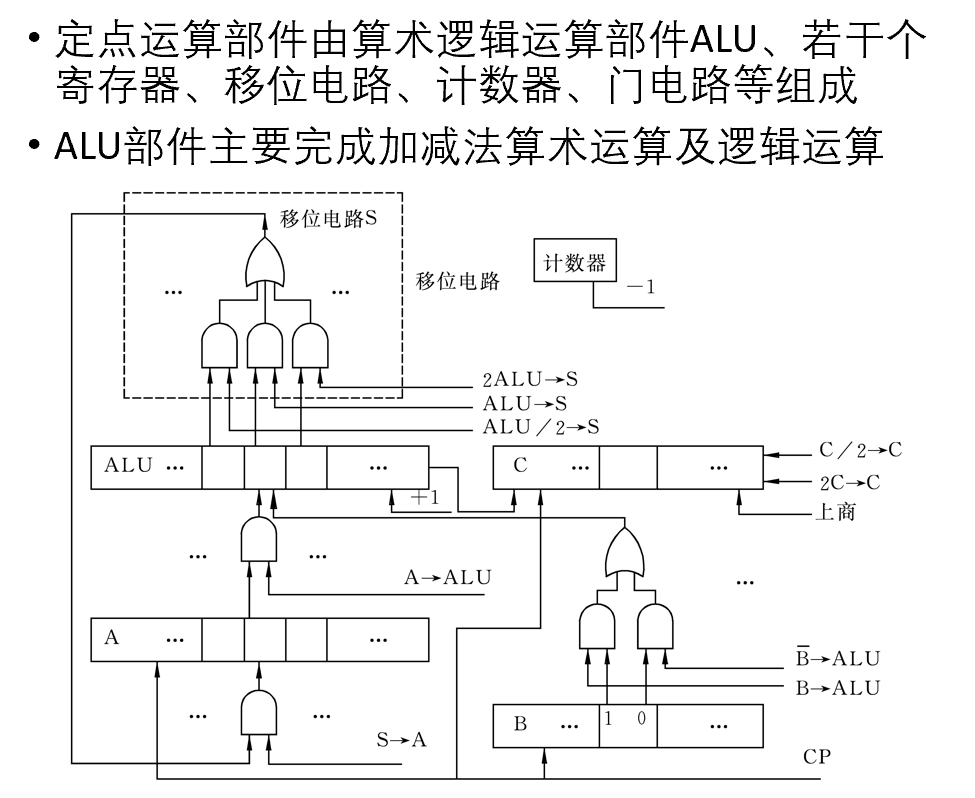
七、运算部件
1.定点运算部件
2.浮点运算部件
八、数据校验码
1.奇偶校验码
- 编码方法:

- 特点:

- 例:
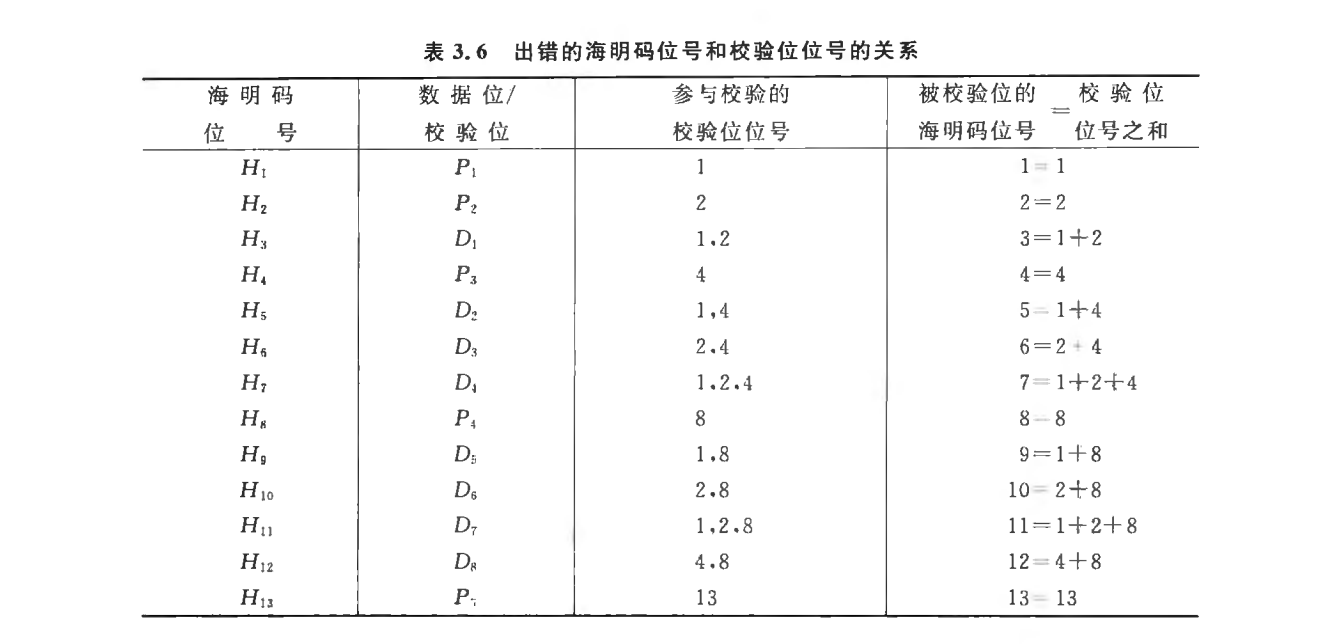
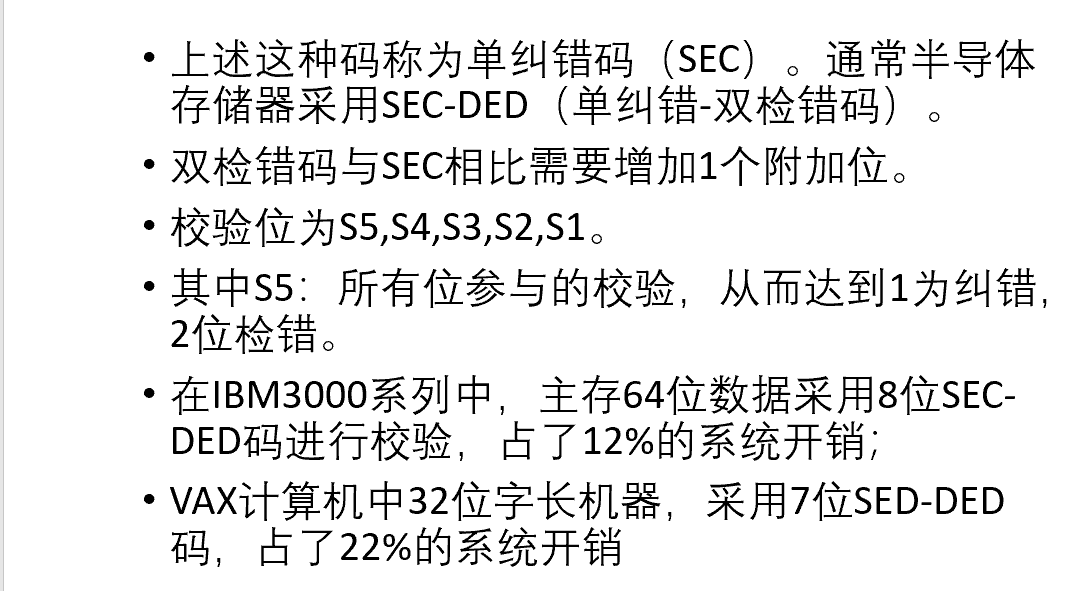
2.海明校验码
-
编码方法:


-
特点:可以发现2位错,并且能指出哪一位出错
-
例:


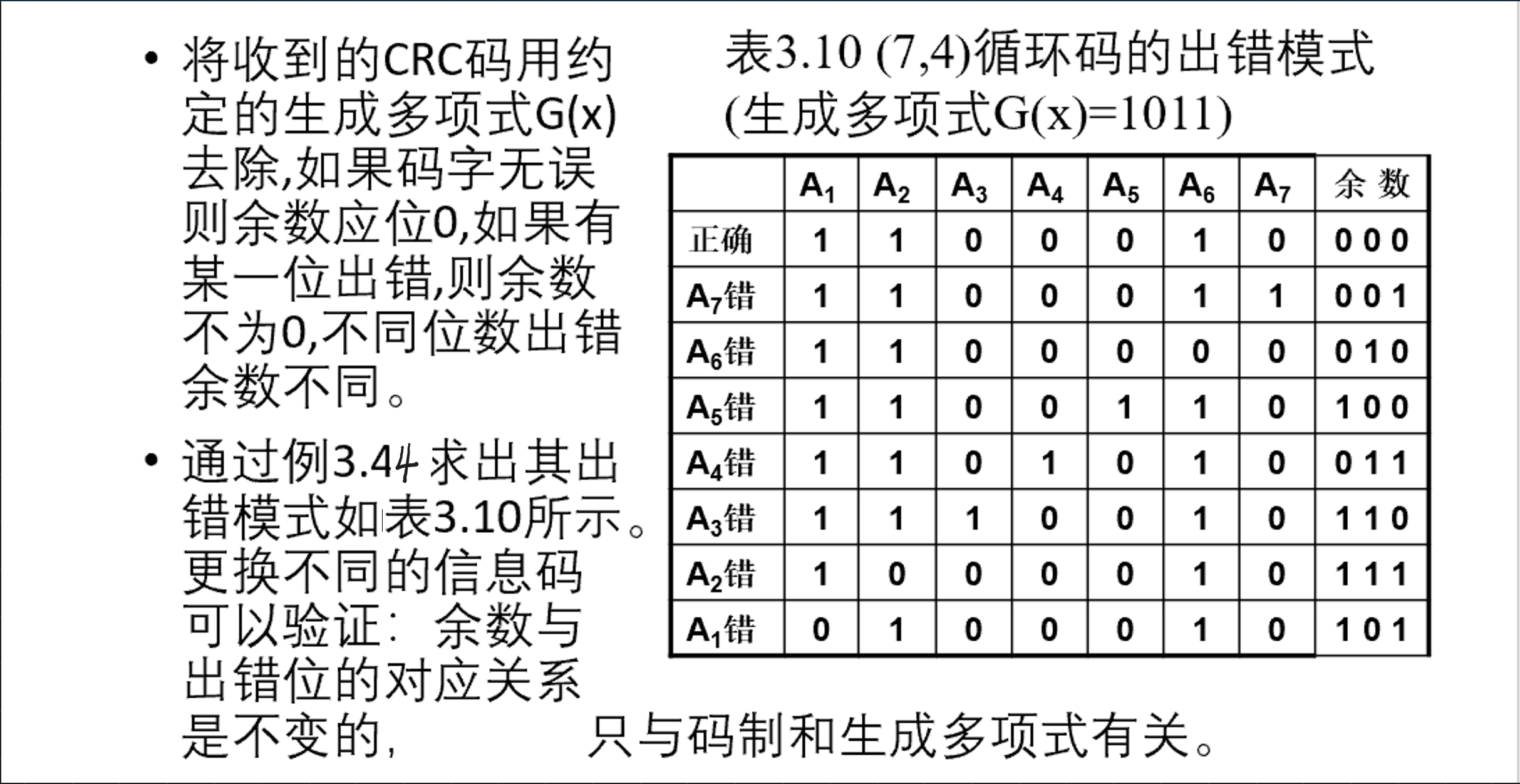
3.循环冗余校验(CRC)码
-
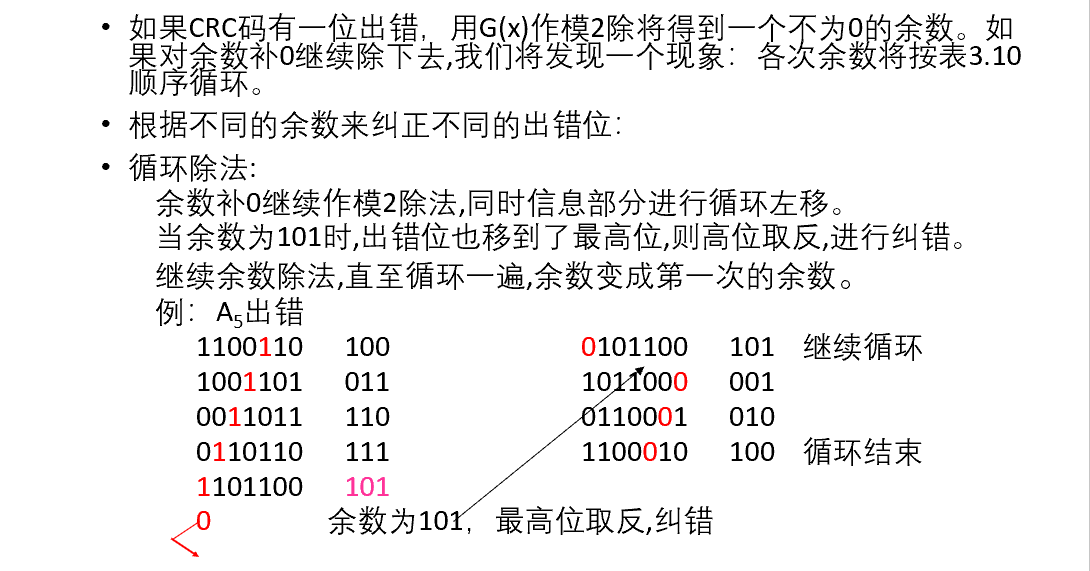
编码方法:



-
例:


参考-《计算机组成于结构》-清华大学 王爱英