代码:
void BFS(MGraph Graph, Vertex S, void(* Visit)(Vertex))
{
Queue Q;
Vertex V, W;
Q = CreateQueue(MaxSize); // 创建空队列
// 访问顶点, 此处可以根据需要改写 Visit 函数
Visit(S);
Visited[S] = true; // 标记 S 已访问
AddQ(Q, S); // S 入队
while (!IsEmpty(Q))
{
V = DeleteQ(Q); // 弹出 V
for (W = 0; W < Graph->Nv; W++) // 对图中的每个顶点
{
// 若 W 是 V 的邻接点并且未访问过
if (!Visited[W] && IsEdge(Graph, V, W)) {
// 访问顶点 W
Visit(W);
Visited[W] = true; // 标记 W 已访问
AddQ(Q, W); // W 入队
}
}
}
}
配套教程 --> 浙江大学陈越数据结构图部分, 教材 --> 《数据结构第二版》(陈越)
完整代码(这里的图用的是邻接矩阵的实现):
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include "string.h"
#include "queue.h"
#define MaxSize 100
#define MaxVertexNum 100 // 最大顶点数设为 100
#define INFINITY 65535 // 无穷大设为双字节无符号整数的最大值 65535
typedef int Vertex; // 用顶点下标表示顶点, 为整型
typedef int WeightType; // 边的权值设为整型
typedef char DataType; // 顶点存的数据类型设为字符型
// 全局变量 Visited[], 初始化为 false
bool Visited[MaxVertexNum]; // 0 代表 false, 1 代表 true
static void init()
{
memset(Visited, 0, MaxVertexNum);
}
// 图节点的定义
typedef struct GNode * PtrToGNode;
struct GNode {
int Nv; // 顶点数
int Ne; // 边数
WeightType G[MaxVertexNum][MaxVertexNum]; // 邻接矩阵
DataType Data[MaxVertexNum]; // 存顶点的数据
/* 注意: 若顶点无数据, 此时 Data[] 可以不用出现 */
};
typedef PtrToGNode MGraph;
// 边的定义
typedef struct ENode * PtrToENode;
struct ENode {
Vertex V1, V2; // 有向边 <v1, V2>
WeightType Weight; // 权重
};
typedef PtrToENode Edge;
MGraph CreateGraph(int VertexNum)
{
// 初始化一个有 VertexNum 个顶点但没有边的图
Vertex V, W;
MGraph Graph;
Graph = (MGraph) malloc(sizeof(struct GNode)); // 建立图
Graph->Nv = VertexNum;
Graph->Ne = 0;
// 初始化邻接矩阵
// 注意: 这里默认顶点编号是从 0 开始, 到 (Graph->Nv - 1)
for (V = 0; V < Graph->Nv; V++)
for (W = 0; W < Graph->Nv; W++)
Graph->G[V][W] = INFINITY;
return Graph;
}
void InsertEdge(MGraph Graph, Edge E)
{
// 插入边 <V1, V2>
Graph->G[E->V1][E->V2] = E->Weight;
// 若是无向图, 还要插入边 <V2, V1>
// Graph->G[E->V2][E->V1] = E->Weight;
}
MGraph BuildGraph()
{
MGraph Graph;
Edge E;
// Vertex V;
int Nv, i;
scanf("%d", &Nv); // 读入顶点个数
Graph = CreateGraph(Nv); // 初始化有 Nv 个顶点但没有边的图
scanf("%d", &(Graph->Ne)); // 读入边数
if (Graph->Ne != 0) // 如果有边
{
E = (Edge)malloc(sizeof(struct ENode)); // 建立边节点
// 读入边, 格式为 "起点 终点 权重", 插入邻接矩阵
for (i = 0; i < Graph->Ne; i++) {
scanf("%d %d %d", &E->V1, &E->V2, &E->Weight);
// 注意: 如果权重不是整型, Weight 的读入格式要改
InsertEdge(Graph, E);
}
}
// 如果顶点有数据的话, 读入数据
/*for (V = 0; V < Graph->Nv; V++)
scanf("%c", &(Graph->Data[V]));*/
return Graph;
}
// 简单遍历图
void PrintGraph(MGraph G)
{
int i, j;
for (i = 0; i < G->Nv; i++)
{
for (j = 0; j < G->Nv; j++)
{
if (G->G[i][j] == INFINITY)
{
printf("∞ ");
continue;
}
printf("%d ", G->G[i][j]);
}
printf("
");
}
}
bool IsEdge(MGraph Graph, Vertex V, Vertex W)
{
return Graph->G[V][W] < INFINITY ? true : false;
}
void Visit(Vertex V)
{
printf("正在访问顶点%d
", V);
}
void BFS(MGraph Graph, Vertex S, void(* Visit)(Vertex))
{
Queue Q;
Vertex V, W;
Q = CreateQueue(MaxSize); // 创建空队列
// 访问顶点, 此处可以根据需要改写 Visit 函数
Visit(S);
Visited[S] = true; // 标记 S 已访问
AddQ(Q, S); // S 入队
while (!IsEmpty(Q))
{
V = DeleteQ(Q); // 弹出 V
for (W = 0; W < Graph->Nv; W++) // 对图中的每个顶点
{
// 若 W 是 V 的邻接点并且未访问过
if (!Visited[W] && IsEdge(Graph, V, W)) {
// 访问顶点 W
Visit(W);
Visited[W] = true; // 标记 W 已访问
AddQ(Q, W); // W 入队
}
}
}
}
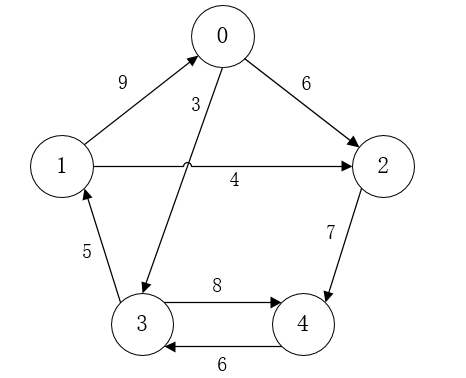
// 测试一组数据, 测试的图有 5 个顶点, 8 条有向边
// <1, 0, 9> <0, 2, 6> <2, 4, 7> <4, 3, 6> <3, 1, 5> <1, 2, 4> <0, 3, 3> <3, 4, 8>
int main()
{
/*---------- 初始测试 ----------*/
/*MGraph G = BuildGraph();
PrintGraph(G);*/
/*---------- 初始测试 ----------*/
/*---------- 测试 BFS ----------*/
MGraph G = BuildGraph();
BFS(G, 0, Visit);
/*---------- 测试 BFS ----------*/
return 0;
}
// 测试数据
/*
5
8
1 0 9
0 2 6
2 4 7
4 3 6
3 1 5
1 2 4
0 3 3
3 4 8
*/
输出结果:
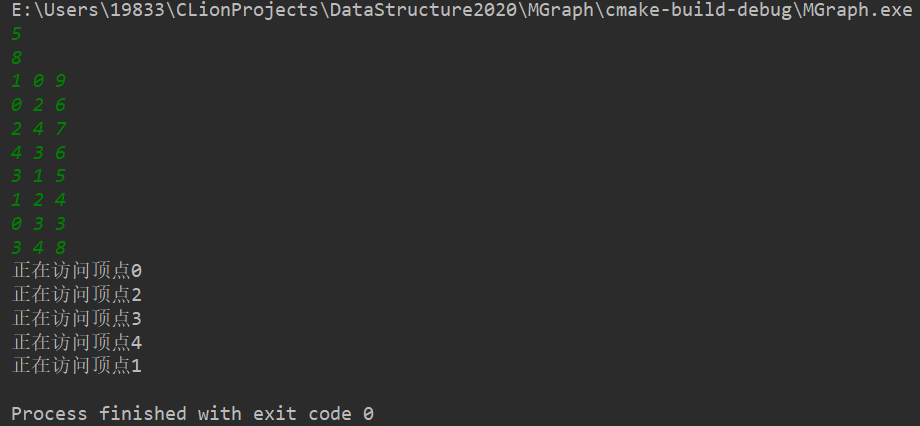
按1: 测试用的图的示意 -->
按2: 代码中所用的队列 --> https://www.cnblogs.com/fanlumaster/p/14016183.html