1.二叉树(BinaryTree):每个节点最多有两个分支(分支的度小于2)的树结构,可为空树,如下所示。
2.完全二叉树(Complete Binary Tree):在一棵二叉树中,除了最后一层,都是满的,并且最后一层或者是满的,或者是右边缺少连续若干节点,成为完全二叉树,如图所示:
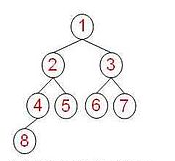
具有k个节点的完全二叉树深度为log2(k)+1
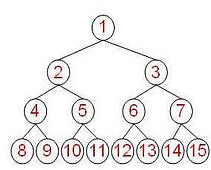
3.满二叉树(Full Tree):一棵深度为k,并且有![]() 个节点的二叉树,成为满二叉树,如图所示:
个节点的二叉树,成为满二叉树,如图所示:
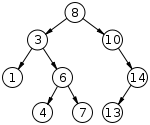
4.二叉查找树(Binary Search Tree):又称为二叉搜索树,排序二叉树,可为空树,或节点满足左子树所有节点<跟节点<右子树所以节点,不存在相等值的节点,如图所示:
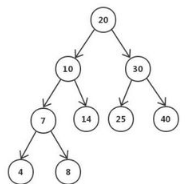
5.平衡二叉树(Balanced Binary Tree):是一种结构平衡的二叉搜索树,即叶子节点深度差不超过1,能够在O(logn)内完成插入、查找和删除操作,结构如图所示,常见的平衡二叉树有AVl树、红黑树等。
6.AVL树:又被称为高度平衡树,是最先发明的自平衡二叉查找树,任何节点的两个儿子子树的高度最大差别为1,增加和删除可能需要通过一次或多次树旋转来重新平衡这个树,树图如图所示。
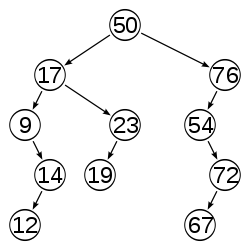
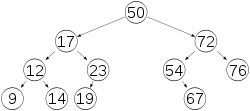
平衡前*(非AVL树) 平衡后(AVL树)
7.红黑树(Red-black tree):是一种自平衡二叉查找树,又称为“对称二叉B树”,除了满足所有二叉查找树的要求之外还需要满足以下要求:
(1)节点是红色或者是黑色的
(2)跟节点是黑色的
(3)每个叶子节点都是黑色的(叶子是NIL节点)
(4)每个红色节点必须有两个黑色节点(从叶子到根节点的所有简单路径上不可能有两个连续的红色节点)
(5)从任一节点到其每个叶子的所有简单路径都饱和相同数目的节点
注:
NIL节点就是空节点,二叉树中庸NIL节点代替NULL
简单路径:指顶点序列中顶点不重复出现的路径

8.线索二叉树:添加了直接指向节点的前驱和后继的指针的二叉树,如图所示:
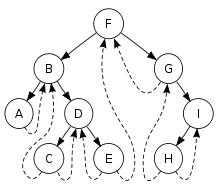
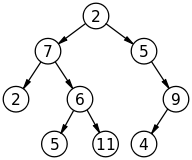
9.哈夫曼树:又称为最优二叉树,是一种带权路径长度最短的二叉树,霍夫曼树构造过程如下:
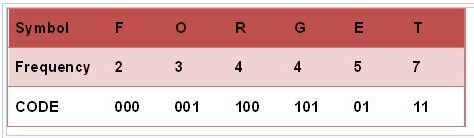
(1).将英文字母按照出现频率从小到大排序,如图所示.
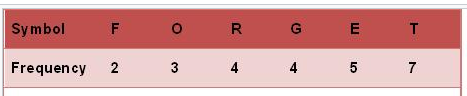
(2)每个字母代表一个终端节点(叶子),比较字母的出现频率,依次选取最小的两个字母组成一个新的节点,如F.O组成节点值为5
(3)比较5.R.G.E.T,发现R与G的频率最小,故相加4+4=8,得到值为8的节点,依次类推构架成树,如图所示
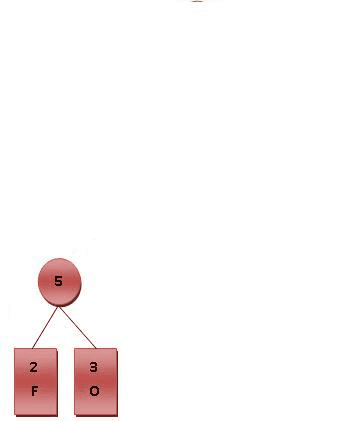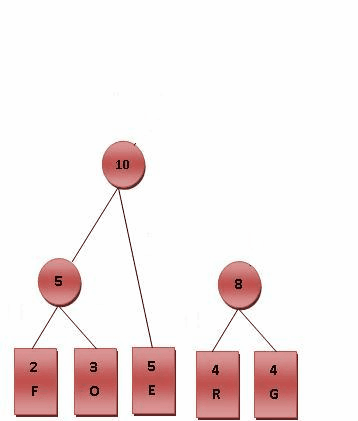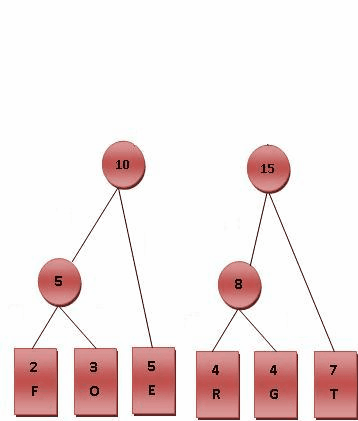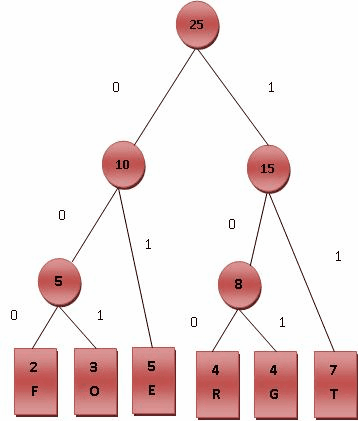
(4)将霍夫曼树的所有左链接置为0,右链接置为1,然后从跟节点到叶子节点分别对所有字母进行编码,完成哈夫曼编码,如图所示