在这里主要讨论两种归一化方法:
1、线性函数归一化(Min-Max scaling)
线性函数将原始数据线性化的方法转换到[0 1]的范围,归一化公式如下:
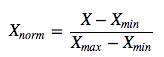
该方法实现对原始数据的等比例缩放,其中Xnorm为归一化后的数据,X为原始数据,Xmax、Xmin分别为原始数据集的最大值和最小值。
python实现:preprocessing.MinMaxScaler
2、0均值标准化(Z-score standardization)
0均值归一化方法将原始数据集归一化为均值为0、方差1的数据集,归一化公式如下:
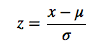
其中,μ、σ分别为原始数据集的均值和方法。该种归一化方式要求原始数据的分布可以近似为高斯分布,否则归一化的效果会变得很糟糕。
python实现:preprocessing.StandardScaler,preprocessing.robust_scale
两种归一化的应用场景:
1、在分类、聚类算法中,需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候,第二种方法(Z-score standardization)表现更好。
2、在不涉及距离度量、协方差计算、数据不符合正太分布的时候,可以使用第一种方法或其他归一化方法。比如图像处理中,将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
为什么在距离度量计算相似性、PCA中使用第二种方法(Z-score standardization)会更好呢?我们进行了以下的推导分析:
归一化方法对方差、协方差的影响:假设数据为2个维度(X、Y),首先看0均值对方差、协方差的影响:
先使用第二种方法进行计算,我们先不做方差归一化,只做0均值化,变换后数据为
![]()
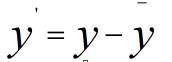
新数据的协方差为
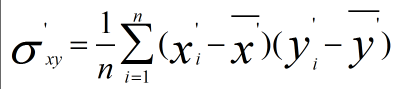
由于
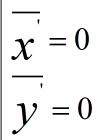
因此

而原始数据协方差为
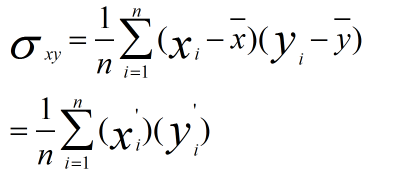
因此
![]()
做方差归一化后:
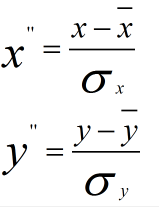
方差归一化后的协方差为:
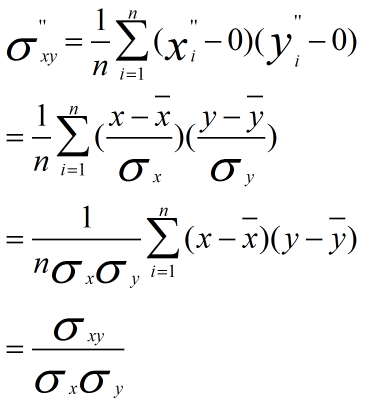
使用第一种方法进行计算,为方便分析,我们只对X维进行线性函数变换

计算协方差
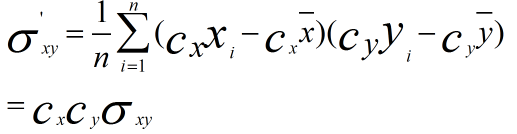
可以看到,使用第一种方法(线性变换后),其协方差产生了倍数值的缩放,因此这种方式无法消除量纲对方差、协方差的影响,对PCA分析影响巨大;同时,由于量纲的存在,使用不同的量纲、距离的计算结果会不同。
而在第二种归一化方式中,新的数据由于对方差进行了归一化,这时候每个维度的量纲其实已经等价了,每个维度都服从均值为0、方差1的正态分布,在计算距离的时候,每个维度都是去量纲化的,避免了不同量纲的选取对距离计算产生的巨大影响。
总结来说,在算法、后续计算中涉及距离度量(聚类分析)或者协方差分析(PCA、LDA等)的,同时数据分布可以近似为状态分布,应当使用0均值的归一化方法。其他应用中更具需要选用合适的归一化方法。