傅里叶变换是一种信号分析方法,让我们对信号的构成和特点进行深入的、定量的研究。把信号通过频谱的方式(包括幅值谱、相位谱和功率谱)进行准确的、定量的描述。
傅里叶变换的核心在于任何信号都可以表示成正弦信号的叠加。

为什么傅里叶变换要把信号分解为正弦波的组合,而不是方波或三角波?
正弦波有个其它任何波形(恒定的直流波形除外)所不具备的特点:正弦波输入至任何线性系统,出来的还是正弦波,改变的仅仅是幅值和相位,即:正弦波输入至线性系统,不会产生新的频率成分(非线性系统如变频器,就会产生新的频率成分,称为谐波)。用单位幅值的不同频率的正弦波输入至某线性系统,记录其输出正弦波的幅值和频率的关系,就得到该系统的幅频特性,记录输出正弦波的相位和频率的关系,就得到该系统的相频特性。
线性系统具备一个特点,多个正弦波叠加后输入至一个系统,输出是所有正弦波独立输入时对应输出的叠加。
也就是说,我们只要研究正弦波的输入输出关系,就可以知道该系统对任意输入信号的响应。
如何求傅里叶变换?
连续傅里叶变换公式如下:

傅里叶的伟大之处不在于如何进行傅里叶变换,而是在于给出了“任何连续周期信号可以由一组适当的正弦曲线组合而成”这一伟大的论断。
正弦函数有一个特点,叫做正交性,所谓正交性,是指任意两个不同频率的正弦波的乘积,在两者的公共周期内的积分等于零。如下:


这是一个非常有用的特性,我们可以利用这个特性设计一个如下的检波器(下称检波器A):
检波器A由一个乘法器和一个积分器构成,乘法器的一个输入为已知频率f的单位幅值正弦波(下称标准正弦信号f),另一个输入为待变换的信号。检波器A的输出只与待变换信号中的频率为f的正弦分量的幅值和相位有关。
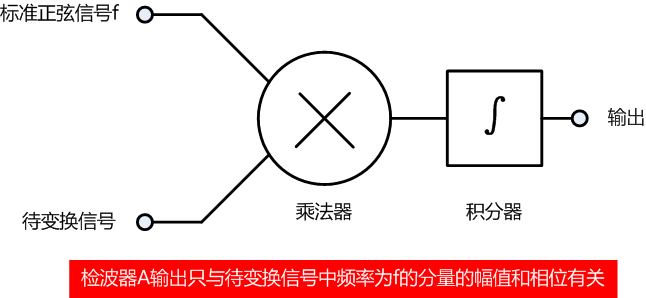
待变换信号可能包含频率为f的分量(下称f分量),也可能不包含f分量,总之,可能包含各种频率分量。一句话,待变换信号是未知的,并且可能很复杂!
因为其它频率分量与标准正弦信号f的乘积的积分都等于零,检波器A可以当它们不存在!经过检波器A,输出就只剩下与f分量有关的一个量,这个量等于待变换信号中f分量与标准正弦信号f的乘积的积分。
很容易得到的结论是:
如果输出不等于零,就说明输入信号包含f分量!
这个输出是否就是f分量呢?
答案:不一定!
正弦波还有下述的特性:
相同频率的正弦波,当相位差为90°时(正交),在一个周期内的乘积的积分值等于零;当相位相同时,积分值达到最大,等于两者的有效值的乘积,当相位相反时,积分值达到最小,等于两者的有效值的乘积取反。
我们知道标准正弦信号f的初始相位为零,但是,我们不知道f分量的初始相位!如果f分量与标准正弦信号f的相位刚好差90°(或270°),检波器A输出也等于零!为此,我们再设计一个检波器B:
检波器B与检波器A的不同之处在于检波器B用一个标准余弦信号f(与标准正弦信号A相位差90°)替代滤波器A中的标准正弦信号f。如果待变换信号中包含f分量,检波器A和检波器B至少有一个输出不等于零。
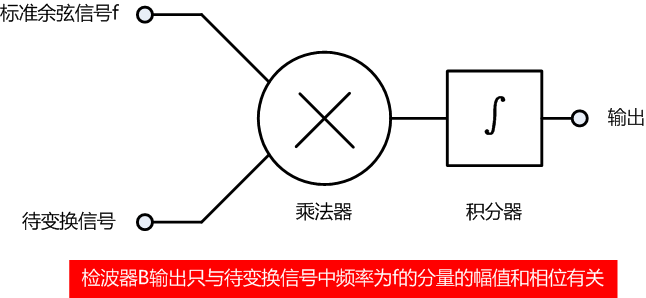
利用三角函数的基础知识可以证明,不论f分量的初始相位如何,检波器A和检波器B输出信号的幅值的方和根就等于f分量的幅值;而检波器B和检波器A的幅值的比值等于f分量初始相位的正切,如此如此……即可求出f分量的相位。
我们再把标准正弦信号f和标准余弦信号f的频率替换成我们关心的任意频率,就可以得到输入信号的各种频率成分。如果知道输入信号的频率,把这个频率作为基波频率f0,用f0、2f0、3f0依次替代标准正弦信号f和标准余弦信号f的频率,就可以得到输入信号的基波、2次谐波和3次谐波。
这就是傅里叶变换!
傅里叶级数


