Egyptian Fractions (HARD version)

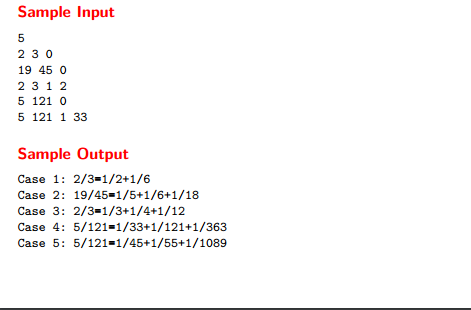
题解:迭代深搜模板题,因为最小个数,以此为乐观估价函数来迭代深搜,就可以了。
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 #include<cstdlib> 7 #define LL long long 8 #define N 10 9 using namespace std; 10 11 LL dep,flag,pre[N],now[N]; 12 bool book[1010]; 13 14 // 函数功能:求最大公约数 15 LL gcd(LL a,LL b){return b?gcd(b,a%b):a;} 16 17 // 函数功能:遍历第dep步的所有解 18 void dfs(LL a,LL b,LL k) 19 { 20 if(b%a==0&&b/a>now[k-1]&&(b/a>1000||!book[b/a])) // 找到符合要求的结果 21 { /* 不要忘记判断最后的结果是否能使用,不然会WA,且要记得b/a的范围在1000以内才能判断,不然会数组越界 */ 22 /* 不能把book放下面判断,没有循环continue不能用,return会出错,可能没有到达dep步b%a==0,但是b/a是不能使用的 */ 23 now[k]=b/a; 24 bool ans=0; 25 for(int i=k;i>=1;i--) 26 { 27 if(now[i]<pre[i]) 28 { 29 ans=1; 30 break; 31 } 32 else if(now[i]>pre[i]) 33 break; 34 } 35 if(!flag||ans) 36 memcpy(pre,now,sizeof(now)); 37 flag=1; 38 return ; 39 } 40 LL s=b/a; 41 if(s<=now[k-1]) s=now[k-1]+1; 42 LL t=(dep-k+1)*b/a; // 迭代搜索执行到第dep步就结束了,限制上界 43 /* 之所以是这个公式是,s是使等式成立最接近的解,把s平均拆分成dep-k+1份,如果没t还小,剩下的dep-k步无论取多少都会偏小 */ 44 if(flag&&t>pre[dep]) t=pre[dep]-1; 45 for(LL i=s;i<=t;i++) 46 { 47 if(i<=1000&&book[i]) // 判断这个点能否使用,不要忘记范围,不要越界访问 48 continue; 49 now[k]=i; 50 LL m=gcd(a*i-b,b*i); 51 dfs((a*i-b)/m,(b*i)/m,k+1); 52 } 53 return; 54 } 55 56 // 函数作用:简洁。可去掉,放在main函数中 57 inline void slove(LL a,LL b) 58 { 59 now[0]=1; 60 for(dep=2;dep<=N;dep++) 61 { 62 dfs(a,b,1); 63 if(flag) 64 { 65 printf("1/%lld",pre[1]); 66 for(LL i=2;i<=dep;i++) 67 printf("+1/%lld",pre[i]); 68 printf(" "); 69 return; 70 } 71 } 72 } 73 74 int main() 75 { 76 int T,cnt=1; 77 scanf("%d",&T); 78 while(T--) 79 { 80 flag=0;memset(book,false,sizeof(book)); 81 LL a,b,k,x; 82 scanf("%lld %lld %lld",&a,&b,&k); 83 while(k--) 84 { 85 scanf("%lld",&x); 86 book[x]=true; 87 } 88 printf("Case %d: %lld/%lld=",cnt++,a,b); 89 slove(a,b); 90 } 91 }