支持向量机(一)：Hard-margin SVM

1.SVM概念（重点：间隔对偶核技巧）

SVM：(support vector machine)，支持向量机，也称最大间隔分类器(max margin classifier)

超平面：实现高维空间中样本的线性可分。超平面公式：w^TX+b=0。

【SVM实现分类的手段是在特征空间中找到一个超平面。超平面可以用w^TX+b表示，构建一个SVM模型最终就是要求出最佳的参数w*和b*。】

间隔：样本到超平面的距离。SVM转化为优化问题就是求出一个超平面，使得离超平面最近的样本的间隔最大。

【距离：几何间隔，函数间隔《统计机器学习》对应章节】

对偶关系转化：max min L<= min max L

【将max L转化为 min L ,求解方便 ，L是拉格朗日乘子式】

核技巧：核函数（kernel function）有两个功能：特征高维转换；求内积。

【一个是将样本的特征空间通过特征转换映射到高维空间以便实现线性可分；】

【另一个功能是能够直接计算出高维数据的内积，避免庞大的计算量。（不同核函数的具体应用：待完成）】

KKT条件：等价于强对偶条件（使等式成立的条件）

SMO算法：SVM的常用实现算法

硬间隔(Hard-margin)：不允许分类错误

软间隔(Soft-margin)：允许一点点分类错误（鲁棒性更强）

2.SVM推导

1）原始问题转化

problem :

max margin

s.t: yi*(w^TX+b)>0 

=max min distance of X

= max min |w^TX+b|/||w||

s.t : yi*(w^TX+b)>0 

→ 【exist r>0 ,yi*(w^TX+b)>=r  meet the constrains → set r=1 → s.t min yi*(w^TX+b)=1】

→ problem: max min |w^TX+b|/||w||

→ max min  yi(w^TX+b)/||w||

→ max  1/||w|| 

→ min 1/2*w^Tw

→ problem : 

min 1/2*w^Tw

s.t  yi*(w^TX+b)>=1

【lagrange 乘子法求解带约束的优化问题：求极值】

【 |w^TX+b|/||w||表示样本x到超平面的距离，max对应参数为w,b，min对应参数为x ；max min L <= min max L为弱对偶关系，若要成为强对偶关系‘=’，有两种情况：①满足KKT条件；②凸优化问题，并且是线性约束】

→ w*

→ 满足KKT条件 

→ 支持向量【在间隔线|w^TX+b|=1上的样本称为支持向量】

→ b*

2）公式推导：

original problem:

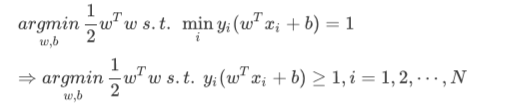
lagrange:

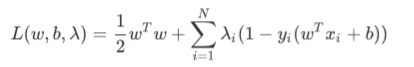
original problem: 【trick: using max to exclude {w,b | 1-yi(wTX+b)>0 } 】

 

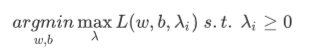
dual problem:

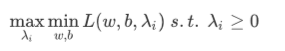
partial_diff_b:

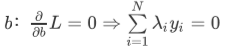
put into L:

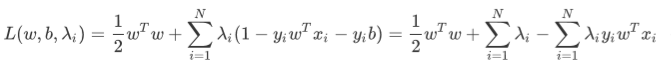
partial_diff_w:

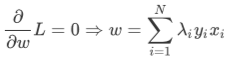
get L: (with w(λ)，b(λ)) 

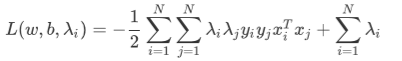
get dual problem:

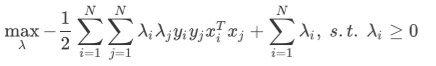
KKT：

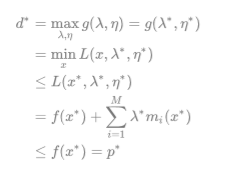
d*为对偶问题；p*为原问题；

梯度为零时，第一个不等号取等号；

满足互补松弛条件λ(1-yi(w^TX+b))=0时，第二个不等号取等号；

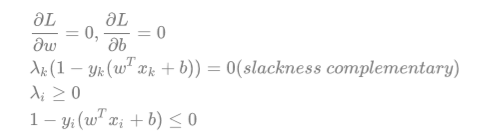
于是这个超平⾯的参数w就是数据点的线性组合，

最终的参数值就是部分满⾜互补松弛条件的向量的线性组合，这些向量也叫支持向量。

w*,b*: 【only depend on support vector → support vector machine】

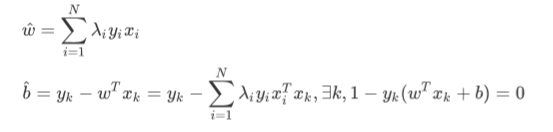
get xi^Txk:

using kernel function.

3.Hard SVM代码

参考资料：

1.https://www.bilibili.com/video/BV1Hs411w7ci?from=search&seid=1584423692713473845 ,作者：shuhuai008 

1.https://www.jianshu.com/p/ba02b92baaaf，作者：老坛酸菜君

2.https://www.zhihu.com/question/31211585/answer/640501555，作者：韦易笑