思路分析
最多放3种颜色
1.贪心放,与之前类型同,就放同一种颜色,不同就放与前面相反的颜色。 (颜色1 或者 颜色0)
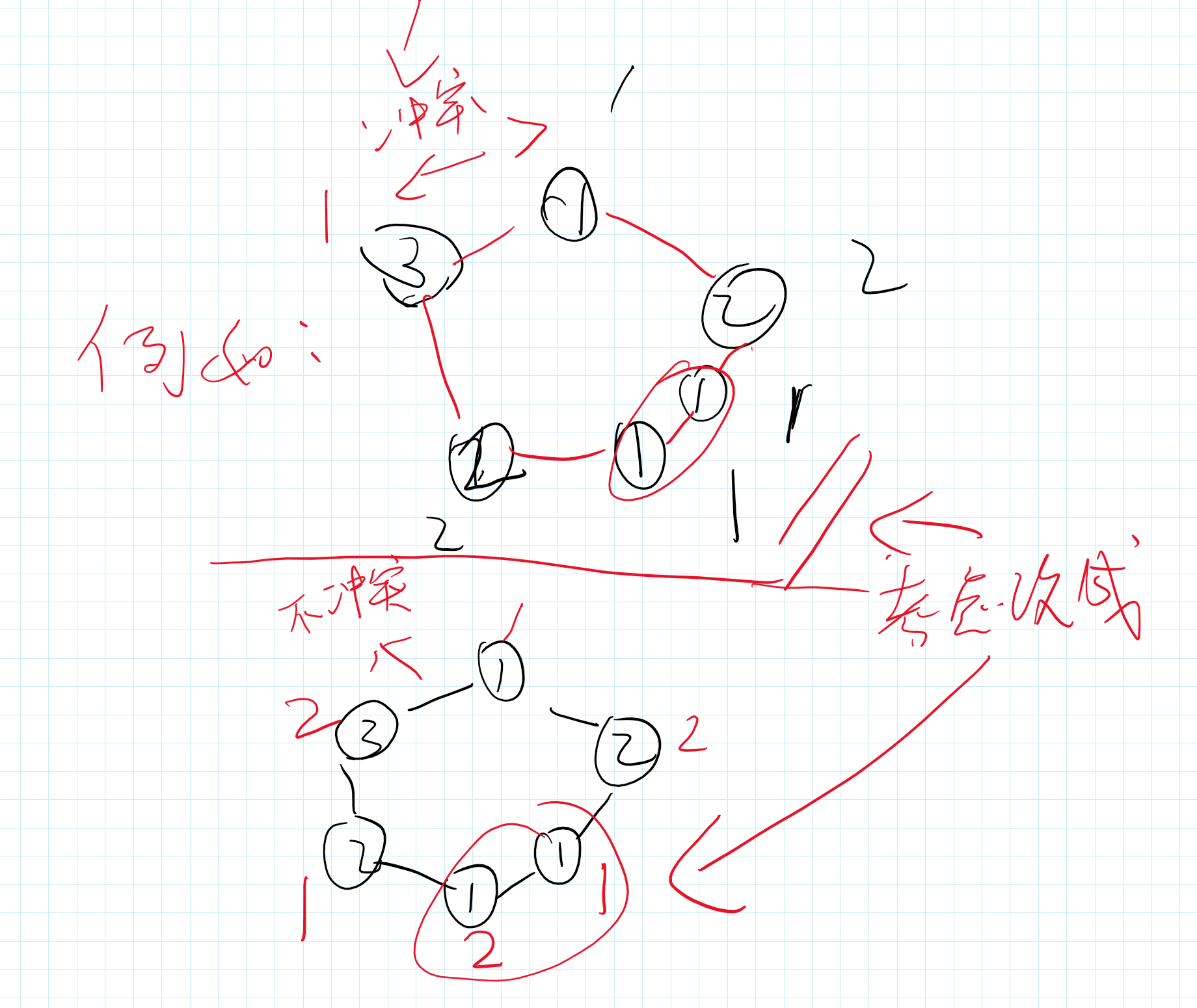
2.考虑最后1个的颜色方案:如果最后1个与第一个类型不相同,颜色却相同,即产生了颜色冲突,那么我们把最后的颜色改成(颜色2)(唯一)就肯定可以。
3.这样wa了,那么肯定是最后1个元素出问题了。再考虑最后1个颜色的方案有没有更优的方法,因为不一定改成颜色2就更优;想到:我们之前贪心忽略了相邻的同种类型放相同颜色对后面的影响,如果我们把这两个颜色中的其中1个改为相反的颜色,为了不影响后面的颜色,后面的颜色都需要变为相反的颜色,这样再贪心放到最后的n时,就不会和1产生冲突(前面已经冲突过了,改成另一种相反颜色肯定不冲突了)。
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e5+100;
int t;
int a[maxn];
int b[maxn];
void solve(){
int n;
cin>>n;
for(int i=1;i<=n;i++) b[i] = 0;
for(int i=1;i<=n;i++) cin>>a[i];
int t = 1;
int pos = 0;
b[1] = 0;
//贪心放
for(int i=2;i<=n;i++){
if(a[i] == a[i-1]){
pos = i;
b[i] = b[i-1];
}else{
t = 2;
b[i] = !b[i-1];
}
}
//判最后1个
if(a[n] != a[1] && b[n] == b[1]){ //产生冲突
if(pos != 0){ //在前面值相同的地方,做一次改变;就使得a[1] a[n]不在冲突
for(int i=pos;i<=n;i++) b[i] = !b[i]; //pos后面的元素全部取反,全部取反保证方案仍然正确
}else{
t = 3; //前面不能改变的话,就只能拿一个新的元素了
b[n] = 2;
}
}
cout<<t<<endl;
for(int i=1;i<=n;i++) cout<<b[i]+1<<" ";
cout<<endl;
}
int main(){
cin>>t;
while(t--){
solve();
}
return 0;
}