题目描述
多米诺骨牌有上下2个方块组成,每个方块中有1~6个点。现有排成行的
上方块中点数之和记为S1,下方块中点数之和记为S2,它们的差为|S1-S2|。例如在图8-1中,S1=6+1+1+1=9,S2=1+5+3+2=11,|S1-S2|=2。每个多米诺骨牌可以旋转180°,使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。
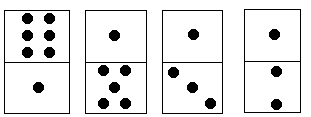
对于图中的例子,只要将最后一个多米诺骨牌旋转180°,可使上下2行点数之差为0。
输入输出格式
输入格式:
输入文件的第一行是一个正整数n(1≤n≤1000),表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数,表示多米诺骨牌上下方块中的点数a和b,且1≤a,b≤6。
输出格式:
输出文件仅一行,包含一个整数。表示求得的最小旋转次数。
输入输出样例
4
6 1
1 5
1 3
1 2
1
Solution:
本题发现每次决策只有两种情况:反转或者不反转。
套上$0/1$背包的模型,考虑枚举差值,由于差值可以为负,所以定义转移时要令其加上一个数$N$又保证不会越界(我这里取得是$N=5000$,因为$1000$个数最多相差$5000$),然后定义状态$f[i][j]$表示取了前$i$个物品差值为$j$的最少交换次数。
则不难想到状态转移方程:设$p$为上面的数减下面的数所得值,则不反转:$f[i][j+p+N]=min(f[i][j+p+N],f[i-1][j+N])$,反转:$f[i][j-p+N]=min(f[i][j-p+N],f[i-1][j+N]+1)$。
初始状态为$f[0][N]=0$(表示取$0$个时差值为$0$的情况不需要交换),其余为$inf$,目标状态为$f[n][i],iin [n-m,n+m]$中的$abs(i-N)$最小时的$f[n][i]$(其中$m$为最大差值,$abs(i-N)$最小时可能对应差值为正和为负两种情况,$f[n][i]$的值要取两者中的最小值)。
代码:
#include<bits/stdc++.h> #define Min(a,b) (a)>(b)?(b):(a) #define For(i,a,b) for(int (i)=(a);(i)<=(b);(i)++) using namespace std; const int N=1000; int n,p,a[N+1][2],f[N+1][10005],m,ans; int main(){ ios::sync_with_stdio(0); cin>>n;m=n*5; For(i,1,n)cin>>a[i][0]>>a[i][1]; memset(f,0x3f,sizeof(f));f[0][N*5]=0; For(i,1,n) For(j,-m,m) p=a[i][0]-a[i][1], f[i][j+p+N*5]=Min(f[i][j+p+N*5],f[i-1][j+N*5]), p=a[i][1]-a[i][0], f[i][j+p+N*5]=Min(f[i][j+p+N*5],f[i-1][j+N*5]+1); p=520520; For(i,N*5-m,N*5+m) if(f[n][i]!=f[0][0]){ if(p>abs(i-N*5))p=abs(i-N*5),ans=f[n][i]; else if(p==abs(i-N*5))ans=Min(f[n][i],ans); } cout<<ans; return 0; }