题目描述
峰值元素是指其值大于左右相邻值的元素。
给定一个输入数组 nums,其中 nums[i] ≠ nums[i+1],找到峰值元素并返回其索引。
数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞。
示例:
输入: nums = [1,2,3,1]
输出: 2
解释: 3 是峰值元素,你的函数应该返回其索引 2。
输入: nums = [1,2,1,3,5,6,4]
输出: 1 或 5
解释: 你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
说明:
- 你的解法应该是 O(logN) 时间复杂度的。
题目链接: https://leetcode-cn.com/problems/find-peak-element/
思路
题目要求时间复杂度为 O(logn) 的意思是让我们使用二分查找求解。因为数组中可能包含多个峰值,我们拿一个峰值为例。假设如下
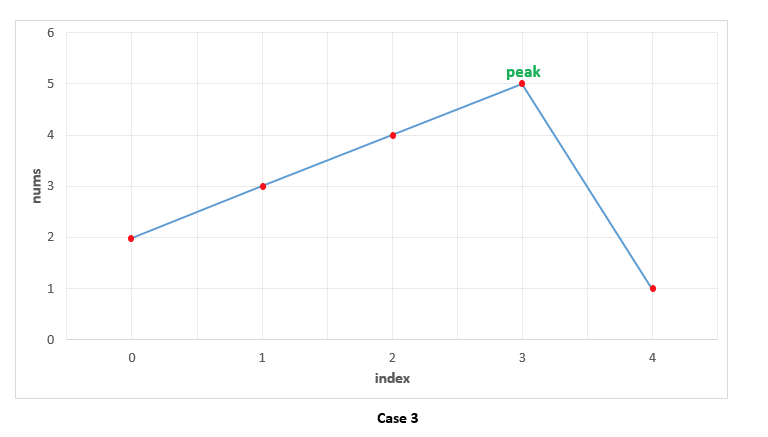
图来自官方题解。
初始时令 left = 0, right = nums.size()-1,mid = (left+right)/2:
- 如果 left<=right,循环:
- mid = (left+right)/2;
- 如果 nums[mid]<nums[mid+1],说明 mid 现在在左边的上坡,峰值在 mid 右边,所以更新 mid = left+1;
- 否则,说明 mid 在右边的下坡,峰值在 mid 的左边,所以更新 mid = right-1(更新为 right-1 而不是 right 的原因是循环条件是 left<=right,根据二分查找的思想来写就行);
left 就是最后的答案。
代码如下:
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0;
int right = nums.size()-1;
while(left<=right){
int mid = left + (right-left)/2;
if(mid+1<nums.size() && nums[mid]<nums[mid+1]){
left = mid+1;
}else right = mid-1;
}
return left;
}
};
- 时间复杂度:O(logn)
- 空间复杂度:O(1)
相关题目
1、山脉数组中查找目标值:https://www.cnblogs.com/flix/p/12805982.html