P1478 陶陶摘苹果（升级版）

题目链接

https://www.luogu.org/problemnew/show/P1478

题解来源：https://www.luogu.org/problemnew/solution/P1478

题目描述（简化）

n个苹果，s点体力，可以摘到苹果的高度为(a + b)。

输入

第1行：两个数 苹果数n，力气s。

第2行：两个数 椅子的高度a，陶陶手伸直的最大长度b。

第3行~第3+n-1行：每行两个数 苹果高度xi，摘这个苹果需要的力气yi。

输出：

只有一个整数，表示陶陶最多能摘到的苹果数

题解

1.搜索

搜索是一种很基本的算法，很多算法或多或少都是建立在搜索的基础上的。搜索思路简单，适用性广，如果不存在时间或空间的限制的话，基本上没有搜索解不了的题。

但是搜索的缺点也同样明显，由于它过于基础，难免有点粗枝大条，DFS容易TLE（运行超时），BFS容易MLE（运行内存超空间），有时DFS还面临着递归层数过多爆栈的风险……

我们在这里重点讲DFS搜索优化，BFS做法暂且先不讲了。

（1）第一版:无优化写法

搜索之所以可以被广泛地被使用于各种题目，就是因为它思路简单，实现容易。

搜索的基本思路就是枚举，枚举可能出现的各种情况，然后从中找到满足条件的结果。

对于这个题，朴素的搜索方法就是DFS搜索每个苹果，每个苹果可分支出两个搜索子树：摘这个苹果或者不摘这个苹果。比如这样的一棵搜索树：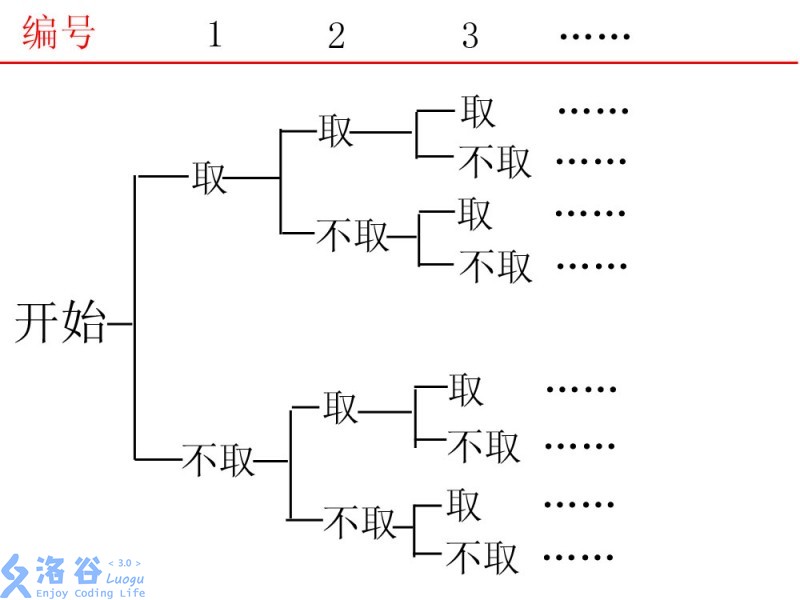 

那我们的代码实现也很简单：

我们使用递归函数，从第一个苹果开始递归访问，如果这个苹果可以取（高度够得到或者当前剩下的体力还够用），则递归搜索取这个苹果的子树。然后无论能不能取都递归搜索不取这个苹果的子树。

当搜索到叶子节点也就是第n+1个苹果（这个苹果并不存在）的时候，返回0。对于其他苹果节点，返回两个搜索子树返回值中的较大值（只有一个则返回那个值）。

那么函数的返回值是什么意思呢？返回值表示这个苹果的搜索子树里的最大能取的苹果数量。

具体的代码实现可以参考下面这份代码（这份代码并不能通过）：

#include<iostream>
using namespace std;
int n,s,a,b,ans;
int xi[5005],yi[5005];
int dfs(int num,int rest){
    if(num>n) return 0;//如果到了第n+1个苹果,就说明DFS递归到底了
    int maxn=0;
    if(xi[num]<=a+b&&rest>=yi[num]){
        maxn=dfs(num+1,rest-yi[num])+1>dfs(num+1,rest)?dfs(num+1,rest-yi[num])+1:dfs(num+1,rest);//dfs()+1表示取当前搜索到的苹果，因此摘到苹果的总数+1
    }//返回两个搜索子树里最大值的较大值
    return maxn;
}
int main(){
    cin>>n>>s>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>xi[i]>>yi[i];
    }
    cout<<dfs(1,s);//从第一个苹果开始递归求解
    return 0;
} 

但是这个代码如果你提交的话，就会完美的TLE掉。我们看一下这个题的数据范围，n最大有5000个，每个苹果有取或不取两个选择，那么搜索完所有的子树差不多就是2^{5000}次运算。而计算机一秒只能运算大约10^7次左右，当然会TLE了。

这种最朴素的搜索算法时间复杂度差不多是O(2^n)的……几乎绝大部分的题目的较大的数据都过不去……那么我们有什么好办法吗？确实存在方法——剪枝和记忆化搜索。

（2）第二版:优化写法

所谓剪枝，就是将对答案没有贡献的搜索子树剪去，从而减少搜索次数，提高运行速度的一种搜索优化方法。剪枝对于DFS的优化效果比较明显，上面一版代码的运行时间跑到了3500多毫秒，但是优化后113毫秒就跑完了（虽然这样还不是最快）。那这90%左右的时间是怎么优化掉的呢？

首先先不去考虑剪枝那么难的东西，大家有没有注意到上面的代码里有这么一行：

maxn=dfs(num+1,rest-yi[num])+1>dfs(num+1,rest)?dfs(num+1,rest-yi[num])+1:dfs(num+1,rest);

我们要知道，如果想得到一个函数的返回值，首先就要运行一遍这个函数。复杂度如此高的函数在比较和调用值的时候分别运算了一次，就相当于给搜索树凭空加了好多无用的搜索子树。那么我们能不能用两个个变量来存储dfs(num+1,rest-yi[num])dfs(num+1,rest−yi[num])和dfs(num+1,rest)dfs(num+1,rest)的值呢？这样经过测试可以节省大约30%的时间。代码如下：

#include<iostream>
using namespace std;
int n,s,a,b,ans;
int xi[5005],yi[5005];
int dfs(int num,int rest){
    if(num>n) return 0;
    int maxn=dfs(num+1,rest);
    if(xi[num]<=a+b&&rest>=yi[num]){
        int t=dfs(num+1,rest-yi[num])+1;
        maxn=t>maxn?t:maxn;
    }
    return maxn;
}
int main(){
    cin>>n>>s>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>xi[i]>>yi[i];
    }
    cout<<dfs(1,s);
    return 0;
} 

但是这还远远不够，那么剩下的时间是从哪里优化出来的呢？这里就要用到记忆化搜索了。

我们回想一下刚才的改动，就是用两个变量存储了函数的返回值从而避免了函数因为两次调用而做无用功。那么我们自然而然地想到，假如某个函数可能以相同的参量被调用多次的话，那么多调用的这几次不就也是浪费了吗？那么有没有这样的情况呢？有的。大家如果在每个DFS函数的最后加一句：

cout<<"num:"<<num<<" rest:"<<rest<<endl;

就会发现在输出的每次调用的函数中，有很多次调用的num和rest是相同的，这就说明我们做了很多无用功。那么怎么优化呢？这时候记忆化搜索就闪亮登场了：

所谓记忆化搜索，就是将每个不同参量的函数的返回值存在一个数组里，当再次调用这个函数的时候，就不用再次费时间计算这个函数的返回值了。这里我们还是结合代码讲一下：

#include<iostream>
using namespace std;
int n,s,a,b,ans;
int xi[5005],yi[5005];
bool visit[5005][1001];//存储是否访问过调用这两个参量的函数
int mem[5005][1001];//存储调用这两个参量的函数的返回值
int dfs(int num,int rest){
    if(num>n) return 0;
    if(visit[num][rest]) return mem[num][rest];//如果调用这两个参量的函数已经被访问过，那么直接返回之前存储的值即可
    visit[num][rest]=true;
    int maxn=dfs(num+1,rest);
    if(xi[num]<=a+b&&rest>=yi[num]){
        int  t=dfs(num+1,rest-yi[num])+1;
        maxn=t>maxn?t:maxn;
    }
    return mem[num][rest]=maxn;//返回值的同时存储这次运算的返回值
}
int main(){
    cin>>n>>s>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>xi[i]>>yi[i];
    }
    cout<<dfs(1,s);
    return 0;
} 

这样的话就减少了很多次不必要的访问和计算，大大加快了运行速度。

接下来讲剪枝。我们不难发现，对于那些不能够采到的苹果，我们搜索它们只会白白浪费时间，那我们就可以将这些苹果排除掉，这样就使得搜索子树被缩小了。这就是剪枝。

我们怎么才能避免搜索到这些苹果被搜索到呢？我们可以将所有的苹果按照高度从矮到高排序（排序的知识在第一弹里讲过，不会的同学可以去看一下）。在这种情况下当我们搜索到一个够不到的苹果时，无论我们再往下搜索多久，我们都不会再搜索到可以够得到的苹果了。这时候我们就可以 return 0 了。代码如下：

#include<iostream>
#include<algorithm> 
using namespace std;
int n,s,a,b,ans;
bool visit[5005][1001];
int mem[5005][1001];
struct apple{
    int xi,yi;
}ap[5005];
int dfs(int num,int rest){
    if(num>n||ap[num].xi>a+b) return 0;//当搜索到够不到的苹果后，就不再继续向下搜索了
    if(visit[num][rest]) return mem[num][rest];
    visit[num][rest]=true;
    int maxn=dfs(num+1,rest);
    if(ap[num].xi<=a+b&&rest>=ap[num].yi){
        int  t=dfs(num+1,rest-ap[num].yi)+1;
        maxn=t>maxn?t:maxn;
    }
    return mem[num][rest]=maxn;
}
int cmp(apple x,apple y){
    return x.xi<y.xi;
}
int main(){
    cin>>n>>s>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>ap[i].xi>>ap[i].yi;
    }
    sort(ap+1,ap+n+1,cmp);//按照高度从矮到高排序
    cout<<dfs(1,s);
    return 0;
} 

这种方法比起剪枝前，又快了大约15%。

---

2.动态规划——背包

我们做题不能只靠搜索，世界上解决这类问题也不是只有搜索这一种算法，要不然还要OI干吗？

于是，有一些特殊的搜索问题就被优化了，并且形成了一类新的算法：动态规划。动态规划的种类很多：有线性动态规划、多维动态规划、区间动态规划等。我们这里先只讲一类特殊的多维动态规划：背包问题。

动态规划最核心的思想就是状态转移。即任何状态的解都可以建立在已知状态的基础上快速求出。这是不是和记忆化搜索有些类似呢？事实上动态规划和记忆化搜索真的差不多，记忆化搜索需要一个数组来存储不同参量的递归函数的返回值，动态规划需要一个状态转移数组来存储已求解的状态的解。而动态规划相比搜索的高明之处就在于，动态规划可以将搜索有向化，而不是漫无目的地遍历搜索每一个可能的状态，相当于自动剪枝。

我们前面讲过，动态规划实质上是对搜索的优化，之前我们搜索，是从前向后递归搜索，根据之后状态返回的值来决定向前返回什么值。而动态规划用的方法恰恰相反，是从前向后递推搜索，根据之前状态传递来的值决定向后传递什么值。这就是动态规划省时的主要原因。

那么接下来我们来讲背包问题。背包问题解决的一类问题是：对于空间有限的背包，和一些有着已知体积与价值的物品，优化取物品策略使得背包里物品的价值总和最大。对于这个题，总力气就是背包的空间，摘每个苹果所需要的力气就是苹果占背包的空间，每个苹果的价值都是1，我们只需让背包里的苹果价值和最大即可。

上面讲到，动态规划的核心是状态的转移，与此相对应的，每类动态规划问题也都有它的状态转移方程，比如背包问题，它的状态转移方程就是：dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])dp[i][j]=max(dp[i−1][j],dp[i−1][j−v[i]]+w[i])。这之中，dp[i][j]dp[i][j]表示对于空间大小为j的背包考虑前i个物品所能得到的最大总价值，v[i]v[i]表示第i个物品的占空间大小，w[i]w[i]表示第i个物品的价值。

不过讲了这么多，大家估计也听烦了，我们先上代码，然后再根据代码讲一下背包问题的解法。代码如下：

#include<iostream> 
using namespace std;
int dp[5005][1001];
int xi[5005],yi[5005],n,s,a,b;
int main(){
    cin>>n>>s>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>xi[i]>>yi[i];
    }
    for(int i=1;i<=n;i++)//枚举考虑每一个苹果
    for(int j=0;j<=s;j++){//枚举背包大小
        dp[i][j]=dp[i-1][j];//不能取就直接转移考虑之前苹果的最大值
        if(xi[i]<=a+b&&j>=yi[i])//如果能够取
        dp[i][j]=dp[i-1][j-yi[i]]+1>dp[i][j]?dp[i-1][j-yi[i]]+1:dp[i][j];//这个就是动态转移方程。max函数运行太慢，我们这里选择三目运算符取较大值
    }
    cout<<dp[n][s];//因为是从前向后递推，因此接收最终答案的位置也从最前面转到了最后面
    return 0;
}

为什么背包问题的状态转移方程是dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])dp[i][j]=max(dp[i−1][j],dp[i−1][j−v[i]]+w[i])呢？我们还是回到之前讲过的知识点：动态规划实质上是对搜索的优化。回想一下我们当时是怎么搜索的？对于搜索到的每个苹果，都有两种选择：取或者不取。不取则对应返回不取这个苹果后剩下的苹果最多能取的个数，取则对应返回取这个苹果后剩下的苹果最多能够取的个数加1。那么我们该如何将这个转化为递推关系呢？

首先我们考虑，当我们取了一个苹果，就相当于把背包里容纳这个苹果的空间分给了这个苹果，剩下的空间再由这个苹果之前（为什么是之前等一下会讲到）的苹果来分。那么不就相当于把背包缩小后再考虑前面的苹果了吗？那么不取就是背包大小不变，由之前的苹果来分这个背包的空间。基于这样的思想，我们就可以比较在当前背包大小下，是取这个苹果更值还是不取这个苹果更值。而缩小背包考虑之前的苹果的工作，在考虑上一个苹果时就已经求解过了。这样就可以不断地考虑一个又一个的苹果，不断地递推下去，最终得到最终的结果。

那么实现思路就是这样的：首先用一个循环枚举每个苹果，然后在考虑每个苹果时，再用一个循环枚举背包大小（为什么要枚举背包大小？——比较最大值时不是要缩小背包吗？这里就是为下一步递推比较做准备），对于每个大小的背包，如果能够取这个苹果（够得着而且当前背包大小装得下这个苹果），就比较取这个苹果和不取这个苹果哪个更值；如果不能取（够不到或者当前背包大小装不下这个苹果），就将这个大小的背包装之前的苹果的最大值传递给这个dp值。这样就得到了上面的代码。现在再回去看看之前的代码，是不是就明白了呢？

---

3.贪心算法

有的同学可能会注意到，我们给的状态转移方程里有一个变量w[i]w[i]，但是在这个题里我们没有用w[i]w[i]，而是直接用1表示，让人对照起来看难免有些别扭。如果你觉得别扭的话，那我要夸奖你，因为一眼就看出了这个问题其实动态规划并不是最优解。

我们最开始用无优化搜索跑了3500多毫秒才跑完，之后记忆化搜索直接提升到130多毫秒，然后剪枝又优化到110多毫秒，之后动态规划直接60多毫秒解决问题。那你以为这就是这个题的极限通过时间了吗？接下来介绍的贪心算法15毫秒就通过了这个题。

贪心算法其实比动态规划算法要低级不少，因为它适用面实在是有点窄。但是对于某些问题，贪心法却能跑出比动态规划快不少的成绩。

那么为什么这个题可以用贪心算法解决呢？我们看一下，在这个题里，所有苹果费力气也就是占背包空间不同，但是价值都是1。背包问题主要是为了解决拿得多却不一定价值最大，拿价值大的却可能装不下其他有价值的东西而使人陷入两难才被发明的算法。对于价值相同体积却不同的物品，我们每次只取体积最小的，不就能在取得当前价值的情况下，最大化剩余空间，从而拿更多苹果了吗？

讲到这里，大家可能就有点明白贪心算法的适用范围了。我之所以先引例，就是因为下面这段话实在有点晦涩难懂：

百度百科定义：贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，关键是贪心策略的选择，选择的贪心策略必须具备无后效性，即某个状态以前的过程不会影响以后的状态，只与当前状态有关。

我语言功底有限，就不再用我贫瘠的语言来给大家详细解释这段话了。总之，这个题，用贪心确实是最优解。这点从时间复杂度上就能看出来：

搜索的基础复杂度（不加优化）是O(k^n)（k指每个节点的选择分支的个数）的，动态规划的基础复杂度是O(nm)（n,m分别指的是物品数量和背包大小），而贪心却只有O(n)。搜索适用范围最广，同样地时间复杂度也最高；动态规划适用范围有所缩小，但是时间复杂度也相应地提高了；贪心算法适用范围极窄，但却拥有极优的时间复杂度。万事万物都是这样，既有长处，又有短处，长短互补，向来如此。

咳咳……扯远了。下面放上贪心算法的代码。这里就不加注释了，大家借此机会锻炼一下自己的读代码能力吧。

#include<iostream>
#include<algorithm> 
using namespace std;
int n,s,a,b,x_,y_,can,rest,ans;
struct apple{
    int xi,yi;
}ap[50005];
int cmp(apple x,apple y){
    return x.yi<y.yi;
}
int main(){
    cin>>n>>s>>a>>b;
    for(int i=1;i<=n;i++){
        cin>>x_>>y_;
        if(x_<=a+b){
            can++;
            ap[can].xi=x_;
            ap[can].yi=y_;
        }
    }
    sort(ap+1,ap+can+1,cmp);
    rest=s;
    ans=0;
    for(int i=1;rest>=ap[i].yi&&i<=can;i++){
        ans++;
        rest-=ap[i].yi;
    }
    cout<<ans;
    return 0;
} 

（myself）

TLE代码

#include <stdio.h>
#define MAX 5003
#define max(a, b) ((a) > (b) ? (a) : (b))
int h_apple[MAX], n_apple[MAX];
int N;
int fun(int n, int s) {
    if (n == N - 1)
        if (n_apple[n] <= s)
            return 1;
        else
            return 0;
    if (n_apple[n] > s)
        return fun(n + 1, s);
    return max(1 + fun(n + 1, s - n_apple[n]), fun(n + 1, s));
}
int main() {
    int i, s, x, y, a, b;
    scanf("%d%d%d%d", &N, &s, &a, &b);
    for (i = 0; i < N; i++) {
        scanf("%d%d", &x, &y);
        if (x > a + b)
            i--, N--;
        else
            h_apple[i] = x, n_apple[i] = y;
    }
    printf("%d", fun(0, s));
    return 0;
}

方法一、动态规划

#include <stdio.h>
#include <stdlib.h>
#define MAX 5003
#define max(a, b) ((a) > (b) ? (a) : (b))
int h_apple[MAX], n_apple[MAX];
int vis[MAX][1003];
int N;
int fun(int n, int s) {
    if (vis[n][s] != -1)
        return vis[n][s];
    int ans;
    if (n == N - 1) {
        if (n_apple[n] <= s)
            ans = 1;
        else
            ans = 0;
    } else if (n_apple[n] > s) {
        ans = fun(n + 1, s);
    } else {
        ans = max(1 + fun(n + 1, s - n_apple[n]), fun(n + 1, s));
    }
    vis[n][s] = ans;
    return vis[n][s];
}
int main() {
    int i, j, s, x, y, a, b;
    scanf("%d%d%d%d", &N, &s, &a, &b);
    for (i = 0; i < N; i++) {
        scanf("%d%d", &x, &y);
        if (x > a + b)
            i--, N--;
        else
            h_apple[i] = x, n_apple[i] = y;
    }
    for (i = 0; i < MAX; i++)
        for (j = 0; j < 1003; j++)
            vis[i][j] = -1;
    if (N == 0)
        printf("0");
    else
        printf("%d", fun(0, s));
    return 0;
}

方法二、贪心

#include <stdio.h>
#include <stdlib.h>
#define MAX 5003

typedef struct {
    int x;
    int y;
}Node;

int cmp(const void *a, const void *b) {
    if ((*(Node *)a).y > (*(Node *)b).y)
        return 1;
    if (((Node *)a)->y < ((Node *)b)->y)
        return -1;
    return 0;
}

int main() {
    Node apple[MAX];
    int i, n, s, a, b, x, y, cnt = 0;
    scanf("%d%d%d%d", &n, &s, &a, &b);
    for (i = 0; i < n; i++) {
        scanf("%d%d", &x, &y);
        if (x > a + b)
            i--, n--;
        else
            apple[i].x = x, apple[i].y = y;
    }
    qsort(apple, n, sizeof(apple[0]), cmp);
    for (i = 0; i < n; i++) {
        if (s < apple[i].y)
            break;
        s -= apple[i].y;
        cnt++;
    }
    printf("%d", cnt);
    return 0;
}

方法三、背包

#include <stdio.h>
#define maxs 1003
#define maxn 5003
#define max(x, y) ((x) > (y) ? (x) : (y)) 
int dp[maxn][maxs];
int apple[maxn];
int main() {
    int i, j, n, s, a, b, x, y;
    scanf("%d%d%d%d", &n, &s, &a, &b);
    for (i = 1; i <= n; i++) {
        scanf("%d%d", &x, &y);
        if (x > a + b)
            i--, n--;
        else
            apple[i] = y;
    }
    for (i = 1; i <= n; i++)
    for (j = 0; j <= s; j++) {
        // 苹果有0个则最多一定只能取0个
        // 背包容量为0却不一定只能取0个，因为苹果所占空间也可能为0（其实这个地方无需考虑）
        if (apple[i] > j) {
            dp[i][j] = dp[i - 1][j];
        } else {
            dp[i][j] = max(1 + dp[i - 1][j - apple[i]], dp[i - 1][j]);
        }
    }
    printf("%d", dp[n][s]);
    return 0;
}