题目大意:
有 (N) 个星球,编号为 (1ldots N)。每个星球有 (M) 座城市,编号为 (1ldots M)。我们将 (e) 星球上的城市 (f) 记作 ((e,\,f))。有两类边,均为双向:
有 (N imes P) 条一类边,每个星球有 (P) 条,编号为 (1) 到 (P)。第 (i) 条边连接城市 ((e,\,a_i))和 ((e,\,b_i)) ,边权为 (c_i)。
有 (M imes Q) 个二类边。每个城市有 (Q) 条,编号为 (1) 到 (Q)。第 (j) 个边连接城市 ((x_j,\,f))和 ((y_j,\,f)) ,边权 (z_j) 。
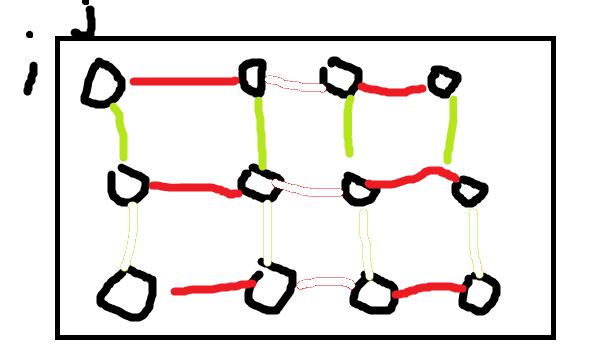
如图所示,红色为一类边,绿色为二类边。请读者注意,这里极易混淆导致下文无法理解
求总边权和-最小生成树边权和。
(0le N,M,P,Qle 10^5),边权最大(10^8)。
题目思路:
首先,我们可以按照题目大意做出最小生成树,这样可以拿到(59 pts)。而剩余测试点会因点数或边数过大而无法通过,因此需考虑优化。
观察一下本题中,(Kruskal)算法运行时的加边过程,可以发现选边时是选一组相同(即所有(a_i b_i c_i)或所有(x_j y_j z_j))的,这里面又是有规律的。我们将一组相同的边统筹起来,并分类考虑。
以下所有叙述均以Kruskal为基础
若当前没有一类边,我们加入二类边,显然要加(m)条。
若当前有一组一类边,那么必定在每个星球中,存在((e,a_i))和((e,b_i))被连接,此时二类边可以不同时在(i)和(j)连边,而是在(i)或(j)连一条边即可,这与同时连边是等价的。因此,仅需加(m-1)条边
若当前有两组一类边,同理,需加(m-2)条边,若当前有(x)组一类边,需加(m-x)条二类边。
而二类边对一类边的影响也是类似的,若有(y)组二类边,需加(n-y)条一类边。
有了这些规律后,我们可以发现不再需要用所有点建最小生成树,而只需要维护一行和一列,建最小生成树即可,即,并查集由(n imes m)变为(n+m),这时建最小生成树可以通过。
上代码
#include<bits/stdc++.h>
using namespace std;
int n,m,p,q,fa[300100],siz;long long s,s1,s2;bool task1;
struct edg
{
long long u,v,len;
}e1[100100],e2[100100];
bool cmp(edg x,edg y)
{
return x.len<y.len;
}
int getfa(int x)
{
if (x==fa[x]) return x;
return fa[x]=getfa(fa[x]);
}
bool hebing(int x,int y)
{
x=getfa(x);y=getfa(y);
if (x!=y)
{
fa[x]=y,siz--;
return true;
}
else return false;
}//并查集
int main()
{
cin>>n>>m>>p>>q;
for (int i=1;i<=p;i++)
{
cin>>e1[i].u>>e1[i].v>>e1[i].len;
s+=e1[i].len*n;
if (e1[i].len!=1) task1=false;
}
for (int i=1;i<=q;i++)
{
cin>>e2[i].u>>e2[i].v>>e2[i].len;
s+=e2[i].len*m;
if (e2[i].len!=1) task1=false;
}
siz=n+m;
for (int i=1;i<=n+m;i++)
{
fa[i]=i;
}
sort(e1+1,e1+p+1,cmp);
sort(e2+1,e2+q+1,cmp);//排序,Kruskal建边
bool f1=false,f2=false;
for (int i=1,j=1;i<=p||j<=q;)
{
if ((i<=p)&&(e1[i].len<e2[j].len||j>q))
{
f1=hebing(e1[i].u,e1[i].v);
if (f1) s-=e1[i].len*(n-s2),s1++;
if (siz==2) break;
i++;continue;
}
else
{
f2=hebing(m+e2[j].u,m+e2[j].v);
if (f2) s-=e2[j].len*(m-s1),s2++;
if (siz==2) break;
j++;continue;
}
}
cout<<s<<endl;
return 0;
}