在最近的项目中,我们涉及到了“内存对齐”技术。对于大部分程序员来说,“内存对齐”对他们来说都应该是“透明的”。“内存对齐”应该是编译器的“管辖范围”。编译器为程序中的每个“数据单元”安排在适当的位置上。但是C语言的一个特点就是太灵活,太强大,它允许你干预“内存对齐”。如果你想了解更加底层的秘密,“内存对齐”对你就不应该再透明了。
一、内存对齐的原因
大部分的参考资料都是如是说的:
1、平台原因(移植原因):不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。
2、性能原因:数据结构(尤其是栈)应该尽可能地在自然边界上对齐。原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访问。
二、对齐规则
每个特定平台上的编译器都有自己的默认“对齐系数”(也叫对齐模数)。程序员可以通过预编译命令#pragma pack(n),n=1,2,4,8,16来改变这一系数,其中的n就是你要指定的“对齐系数”。
规则:
1、数据成员对齐规则:结构(struct)(或联合(union))的数据成员,第一个数据成员放在offset为0的地方,以后每个数据成员的对齐按照#pragma pack指定的数值和这个数据成员自身长度中,比较小的那个进行。
2、结构(或联合)的整体对齐规则:在数据成员完成各自对齐之后,结构(或联合)本身也要进行对齐,对齐将按照#pragma pack指定的数值和结构(或联合)最大数据成员长度中,比较小的那个进行。
3、结合1、2颗推断:当#pragma pack的n值等于或超过所有数据成员长度的时候,这个n值的大小将不产生任何效果。
三、试验
我们通过一系列例子的详细说明来证明这个规则吧!
我试验用的编译器包括GCC 3.4.2和VC6.0的C编译器,平台为Windows XP + Sp2。
我们将用典型的struct对齐来说明。首先我们定义一个struct:
#pragma pack(n) /* n = 1, 2, 4, 8, 16 */
struct test_t {
int a;
char b;
short c;
char d;
};
#pragma pack(n)
首先我们首先确认在试验平台上的各个类型的size,经验证两个编译器的输出均为:
sizeof(char) = 1
sizeof(short) = 2
sizeof(int) = 4
我们的试验过程如下:通过#pragma pack(n)改变“对齐系数”,然后察看sizeof(struct test_t)的值。
1、1字节对齐(#pragma pack(1))
输出结果:sizeof(struct test_t) = 8 [两个编译器输出一致]
分析过程:
1) 成员数据对齐
#pragma pack(1)
struct test_t {
int a; /* 长度4 < 1 按1对齐;起始offset=0 0%1=0;存放位置区间[0,3] */
char b; /* 长度1 = 1 按1对齐;起始offset=4 4%1=0;存放位置区间[4] */
short c; /* 长度2 > 1 按1对齐;起始offset=5 5%1=0;存放位置区间[5,6] */
char d; /* 长度1 = 1 按1对齐;起始offset=7 7%1=0;存放位置区间[7] */
};
#pragma pack()
成员总大小=8
2) 整体对齐
整体对齐系数 = min((max(int,short,char), 1) = 1
整体大小(size)=$(成员总大小) 按 $(整体对齐系数) 圆整 = 8 /* 8%1=0 */ [注1]
2、2字节对齐(#pragma pack(2))
输出结果:sizeof(struct test_t) = 10 [两个编译器输出一致]
分析过程:
1) 成员数据对齐
#pragma pack(2)
struct test_t {
int a; /* 长度4 > 2 按2对齐;起始offset=0 0%2=0;存放位置区间[0,3] */
char b; /* 长度1 < 2 按1对齐;起始offset=4 4%1=0;存放位置区间[4] */
short c; /* 长度2 = 2 按2对齐;起始offset=6 6%2=0;存放位置区间[6,7] */
char d; /* 长度1 < 2 按1对齐;起始offset=8 8%1=0;存放位置区间[8] */
};
#pragma pack()
成员总大小=9
2) 整体对齐
整体对齐系数 = min((max(int,short,char), 2) = 2
整体大小(size)=$(成员总大小) 按 $(整体对齐系数) 圆整 = 10 /* 10%2=0 */
3、4字节对齐(#pragma pack(4))
输出结果:sizeof(struct test_t) = 12 [两个编译器输出一致]
分析过程:
1) 成员数据对齐
#pragma pack(4)
struct test_t {
int a; /* 长度4 = 4 按4对齐;起始offset=0 0%4=0;存放位置区间[0,3] */
char b; /* 长度1 < 4 按1对齐;起始offset=4 4%1=0;存放位置区间[4] */
short c; /* 长度2 < 4 按2对齐;起始offset=6 6%2=0;存放位置区间[6,7] */
char d; /* 长度1 < 4 按1对齐;起始offset=8 8%1=0;存放位置区间[8] */
};
#pragma pack()
成员总大小=9
2) 整体对齐
整体对齐系数 = min((max(int,short,char), 4) = 4
整体大小(size)=$(成员总大小) 按 $(整体对齐系数) 圆整 = 12 /* 12%4=0 */
4、8字节对齐(#pragma pack(8))
输出结果:sizeof(struct test_t) = 12 [两个编译器输出一致]
分析过程:
1) 成员数据对齐
#pragma pack(8)
struct test_t {
int a; /* 长度4 < 8 按4对齐;起始offset=0 0%4=0;存放位置区间[0,3] */
char b; /* 长度1 < 8 按1对齐;起始offset=4 4%1=0;存放位置区间[4] */
short c; /* 长度2 < 8 按2对齐;起始offset=6 6%2=0;存放位置区间[6,7] */
char d; /* 长度1 < 8 按1对齐;起始offset=8 8%1=0;存放位置区间[8] */
};
#pragma pack()
成员总大小=9
2) 整体对齐
整体对齐系数 = min((max(int,short,char), 8) = 4
整体大小(size)=$(成员总大小) 按 $(整体对齐系数) 圆整 = 12 /* 12%4=0 */
5、16字节对齐(#pragma pack(16))
输出结果:sizeof(struct test_t) = 12 [两个编译器输出一致]
分析过程:
1) 成员数据对齐
#pragma pack(16)
struct test_t {
int a; /* 长度4 < 16 按4对齐;起始offset=0 0%4=0;存放位置区间[0,3] */
char b; /* 长度1 < 16 按1对齐;起始offset=4 4%1=0;存放位置区间[4] */
short c; /* 长度2 < 16 按2对齐;起始offset=6 6%2=0;存放位置区间[6,7] */
char d; /* 长度1 < 16 按1对齐;起始offset=8 8%1=0;存放位置区间[8] */
};
#pragma pack()
成员总大小=9
2) 整体对齐
整体对齐系数 = min((max(int,short,char), 16) = 4
整体大小(size)=$(成员总大小) 按 $(整体对齐系数) 圆整 = 12 /* 12%4=0 */
四、结论
8字节和16字节对齐试验证明了“规则”的第3点:“当#pragma pack的n值等于或超过所有数据成员长度的时候,这个n值的大小将不产生任何效果”。另外内存对齐是个很复杂的东西,上面所说的在有些时候也可能不正确。呵呵^_^
[注1]
什么是“圆整”?
举例说明:如上面的8字节对齐中的“整体对齐”,整体大小=9 按 4 圆整 = 12
圆整的过程:从9开始每次加一,看是否能被4整除,这里9,10,11均不能被4整除,到12时可以,则圆整结束。
关于内存对齐的话题,始终是敏感的。稍有不慎,必将闯下大祸!最近项目稍显轻闲,自己给自己安排一天反思和总结一下,突然想到以前写过的一篇'也谈内存对齐',那篇文章谈的是内存对齐的基本知识以及一些实验的数据,想必很多人看完后,会收获一些东西,但是对内存对齐的应用还是处于懵懂状态,其实大部分时间我们是不会显式的用到'内存对齐的',但是有些时候我们需要这样做。这里做了一个小例子,希望能给大家以启发。
例子是这样的:我们有一种二进制文件,其中存储了多条经过特定对齐的某种记录格式的数据,我们的任务就是解析出来这些数据,但是我们不知道也没有这种数据的记录格式结构的定义,但我们不是一无所有,我们有一个表,这个表描述了这个记录格式中有哪些域以及这些域的类型信息,我们还知道的是源数据的对齐系数。
叙述完问题后,我们来给出一些具体的东西:
二进制文件生成程序:
#pragma pack(1)
struct foo_t {
int a;
char b[25];
int c;
};
#pragma pack()
int main() {
FILE *fp = NULL;
struct foo_t foo1 = {12457, "test foo1", 75421};
struct foo_t foo2 = {36098, "test foo2", 89063};
fp = fopen("foo.dat", "wb+");
if (fp == NULL) {
printf("error in open foo.dat!/n");
}
fwrite(&foo1, sizeof(foo1), 1, fp);
fwrite(&foo2, sizeof(foo2), 1, fp);
fclose(fp);
return 0;
}
生成的待解析文件:foo.dat,其中有两条记录。
好了,我们的任务已经很明确了,就是正确解析出这两条记录。如果解析程序知道有下面这样的结构体定义:
#pragma pack(1)
struct foo_t {
int a;
char b[25];
int c;
};
#pragma pack()
那这里也就不用说废话了,我们不知道这个结构定义,不过我们通过知道的一些信息可以整理出一个描述该结构定义的一个表:
#define X_CHAR 1
#define X_STRING 2
#define X_INT 3
typedef struct x_fld_info_t {
char name[MAX_FIELD_NAME_LEN];
int type;
int nitems;
int offset;
} x_fld_info_t;
x_fld_info_t cpi_type_info_tab[3] = { /* cpi - composite */
{"a", X_INT, 1, -1},
{"b", X_STRING, 25, -1},
{"c", X_INT, 1, -1}
};
想一想,我们能从文件foo.dat中读出来什么?仅仅是一块数据,每次读多大一块?如何在这块数据中找到相应的域呢?没错,我们需要通过cpi_type_info_tab这个表信息得出每条foo_t记录的大小,还要得到foo_t中每个域在这块数据中的偏移量,然后根据偏移量和域自身大小准确获取其内容。
好了终于要用到内存对齐的知识了,其实想想也知道foo.dat的文件生成程序和我们的解析程序可能不在一台机器上,而且完全可能在体系结构不同的机器上,这样不同体系结构的机器他们的默认对齐系数、字节序都可能不同(这里我们暂不考虑字节序的问题),我们在文件生成程序那边强制指定对齐系数有利于解析程序这边的解析。我们要做的就是根据已知的对齐系数和cpi_type_info_tab表中的信息计算出来该结构体在特定对齐系数下的总大小以及其各个域的偏移量。下面的宏X_ROUND_UP和函数align_cpi_type配合完成了这一工作:
int x_atom_type_size[4] = {
-1,
sizeof(char),
sizeof(char),
sizeof(int)
};
static int lg2(int k) { /* 这里假设k一定为2的次方^_^ */
int i = 0;
while ((k /= 2) != 0) {
i++;
}
return i;
}
#define X_ROUND_UP(x, k, rv) do { /
unsigned int t = (-1 << k); /
(rv) = ((x - t - 1) & t); /
} while(0)
static void align_cpi_type(x_fld_info_t *tab, int fld_cnt, int force_align_mod, int *size) {
int i = 0;
int cur = 0;
int rv = 0;
int max_sz = 0; /* 复合类型各个域中的最大原子类型的长度, 用于对齐整个结构 */
int atom_sz = 0; /* 域的原子类型 */
int ali_mod = 0; /* alignment modules */
/*
* 对齐各个域
*/
for (i = 0; i < fld_cnt; i++) {
atom_sz = x_atom_type_size[tab[i].type];
if (max_sz < atom_sz) {
max_sz = atom_sz;
}
if (atom_sz < modules) {
ali_mod = atom_sz;
} else {
ali_mod = force_align_mod;
}
X_ROUND_UP(cur, lg2(ali_mod), rv);
tab[i].offset = rv;
cur += (atom_sz * (tab[i].nitems));
}
/*
* 对齐整个复合类型
*/
if (max_sz < force_align_mod) {
ali_mod = max_sz;
} else {
ali_mod = force_align_mod;
}
X_ROUND_UP(cur, lg2(ali_mod), rv);
(*size) = rv;
}
如果对内存对齐还有疑惑的,可以去看看我的那篇'也谈内存对齐',再回到这来看align_cpi_type的实现,这里的X_ROUND_UP的算法借自于'Hacker's Delight'一书,很好的一本讨论'Computer Arithmetic'的书,里面的很多Knowledge & Tip很有价值。通过align_cpi_type函数我们既得到了结构的大小也得到了结构中各个域的偏移量。根据这些信息我们就可以输出文件foo.dat中的数据了。
static void output_cpi_mem(x_fld_info_t *tab, int fld_cnt, char *buf)
{
int i = 0;
int int_tmp = 0;
char str_tmp[50]; /* 这里仅是举例, 所以使用了一个固定大小的缓冲区, 实际上需要做一个可动态扩展的缓冲区 */
for (i = 0; i < fld_cnt; i++) {
if (tab[i].type == X_STRING) {
memset(str_tmp, 0, sizeof(str_tmp));
memcpy(str_tmp, (char*)(buf+(tab[i].offset)), x_atom_type_size[tab[i].type] * (tab[i].nitems));
printf("the value of field '%s' is [%s]/n", tab[i].name, str_tmp);
} else if (tab[i].type == X_INT) {
memcpy(&int_tmp, (char*)(buf+(tab[i].offset)), x_atom_type_size[tab[i].type] * (tab[i].nitems));
printf("the value of field '%s' is [%d]/n", tab[i].name, int_tmp);
}
}
}
int main() {
x_fld_info_t cpi_type_info_tab[3] = { /* cpi - composite */
{"a", X_INT, 1, -1},
{"b", X_STRING, 25, -1},
{"c", X_INT, 1, -1}
};
int size = 0;
int i = 0;
align_cpi_type(cpi_type_info_tab, sizeof(cpi_type_info_tab)/sizeof(cpi_type_info_tab[0]), modules, &size);
/*
* 从文件foo.dat中读出所有记录
* 并打印出来
*/
FILE *fp = NULL;
char buf[50];
fp = fopen("foo.dat", "r");
if (fp == NULL) {
printf("error in fopen!/n");
}
for (i = 0; i < 2; i++) { /* 这里偷了个懒儿,直接用2这个记录的个数了 */
memset(buf, 0, sizeof(buf));
fread(buf, size, 1, fp);
/*
* 通过cpi_type_info_tab中的信息打印出
* 各个字段的值
*/
output_cpi_mem(cpi_type_info_tab, 3, buf);
}
fclose(fp);
return 0;
}
执行输出:
the value of field 'a' is [12457]
the value of field 'b' is [test foo1]
the value of field 'c' is [75421]
the value of field 'a' is [36098]
the value of field 'b' is [test foo2]
the value of field 'c' is [89063]
看到这有些人可能还是很糊涂,到底为什么要这么做呢?提示一下:现在我们要解析一存储未知类型数据的文件的记录时,我们只需要这个纪录的一些描述信息即可了,而无需知道那个foo_t的具体定义了。能不能理解就看你自己了。
记得以前曾经两次谈到过内存对齐话题,一次在'也谈内存对齐'一文中,另一次则是'也谈内存对齐(续)',今天下午和同事又谈到内存对齐的问题了,遂想继续挖掘下去,看看其背后的故事。
关于内存对齐的中文文章多在介绍对齐的'法则',比如为什么sizeof(T)和我们估计的T的大小有出入呢等等,而对于内存对齐的本质少有介绍,我在Google上搜索了一阵后,在IBM开发社区上发现一篇叫'Data alignment: Straighten up and fly right'的文章,其中就有我想知道的关于'内存对齐背后的故事',下面的很多内容都是来自那篇文章的。
很多书籍中都讲到:内存可以看成一个byte数组,我们通过编程语言提供的工具对这个'大数组'中的每个元素进行读写,比如在C中我们可以用指针一次读写一个或者更多个字节,这是我们一般程序员眼中的内存样子。但是从机器角度更具体的说从CPU角度看呢,CPU发出的指令是一个字节一个字节读写内存吗?答案是'否'。CPU是按照'块(chunk)'来读写内存的,块的大小可以是2bytes, 4bytes, 8bytes, 16bytes甚至是32bytes. 这个CPU访问内存采用的块的大小,我们可以称为'内存访问粒度'。
程序员眼中的内存样子:
---------------------------------
| | | | | | | | | | | | | | | | |
---------------------------------
0 1 2 3 4 5 6 7 8 9 A B C D E F (地址)
CPU眼中的内存样子:(以粒度=4为例)
---------------------------------------------
| | | | | | | | | | | | | | | | | | | |
---------------------------------------------
0 1 2 3 4 5 6 7 8 9 A B C D E F (地址)
有了上面的概念,我们来看看粒度对CPU访问内存的影响。
假设这里我们需要的数据分别存储于地址0和地址1起始的连续4个字节的存储器中,我们目的是分别读取这些数据到一个4字节的寄存器中,
如果'内存访问粒度'为1,CPU从地址0开始读取,需要4次访问才能将4个字节读到寄存器中;
同样如果'内存访问粒度'为1,CPU从地址1开始读取,也需要4次访问才能将4个字节读到寄存器中;而且对于这种理想中的''内存访问粒度'为1的CPU,所有地址都是'aligned address'。
如果'内存访问粒度'为2,CPU从地址0开始读取,需要2次访问才能将4个字节读到寄存器中;每次访存都能从'aligned address'起始。
如果'内存访问粒度'为2,CPU从地址1开始读取,相当于内存中数据分布在1,2,3,4三个地址上,由于1不是'aligned address',所以这时CPU要做些其他工作,由于这四个字节分步在三个chunk上,所以CPU需要进行三次访存操作,第一次读取chunk1(即地址0,1上两个字节,而且仅仅地址1上的数据有用),第二次读取chunk2(即地址2,3上两个字节,这两个地址上的数据都有用),最后一次读取chunk3(即地址5,6上两个字节,而且仅仅地址5上的数据有用),最后CPU会将读取的有用的数据做merge操作,然后放到寄存器中。
同理可以推断如果'内存访问粒度'为4,那么从地址1开始读取,需要2次访问,访问后得到的结果merge后放到寄存器中。
是不是所有的CPU都会帮你这么做呢,当然不是。有些厂商的CPU发现你访问unaligned address,就会报错,或者打开调试器或者dump core,比如sun sparc solaris绝对不会容忍你访问unaligned address,都会以一个core结束你的程序的执行。所以一般编译器都会在编译时做相应的优化以保证程序运行时所有数据都是存储在'aligned address'上的,这就是内存对齐的由来。
我们可以指定按照何种粒度访问特定内存块儿:其中void *T为指向特定内存块的地址指针
char *p = (char*)T;每次操作一个字节
short *p = (short*)T;每次操作两个字节
int *p = (int*)T;每次操作4个字节
以此类推。
在'Data alignment: Straighten up and fly right'这篇文章中作者还得出一个结论那就是:"如果访问的地址是unaligned的,那么采用大粒度访问内存有可能比小粒度访问内存还要慢"。
最近在思考改进项目中一模块的实现,该模块维护起来让我很是头疼,所有才有了整体换掉它的想法。设计和实现中利用了内存对齐的技术。关于内存对齐,我曾经写过三篇文章,第一篇介绍了计算内存对齐的方法和例子,第二篇说了一个内存对齐的应用;三谈内存对齐时,则从其本质上做了阐述,而这次实际上是继续在其本质上的做文章,结合本质谈谈为什么内存对齐的计算方法就应该是第一篇中所讲的那两条。
如果对内存对齐本质还不清楚的话,就看看我的内存对齐系列的第三篇吧。如果你清楚了本质,那么我们结合第一篇中交待的内存对齐计算方法来进一步探究,为什么计算的方法就是这个样子的。
再理解一下对齐系数/模数,众所周知Alignment module反映了CPU 取数据时对数据起始地址的限制-这个地址值必须能被Alignment module所整除,但继续仔细考虑下去,你会想到CPU在下一次取数据依然要从下一个能被Alignment module所整除的地址的地方去取,这显而易见,又能说明什么呢?如果说CPU第一次取数据的地址是first_read_address,那么连续下一次的地址就应该是first_read_address + Alignment module了,也就是说每次取数据的量就是Alignment module这么多,这样通过Alignment module我们又可以知道一个量,那就是:在Alignement module限制下,CPU一次能取Alignment module个字节;在“Data alignment: Straighten up and fly right”一文中作者也称之为"memory access granularity"。从应用层开发人员的角度理解:被访问变量的长度,就是CPU要去读取的字节数;而对齐系数又是限制CPU读取字节数的一个指标,有了这两个理解,解决下面的疑问就有了基础了。
在'也谈内存对齐'一篇中介绍了内存对齐的计算方法,这里不妨再引用一下:
1、数据成员对齐规则:结构(struct)(或联合(union))的数据成员,第一个数据成员放在offset为0的地方,以后每个数据成员的对齐按照#pragma pack指定的数值和这个数据成员自身长度中,比较小的那个进行。
2、结构(或联合)的整体对齐规则:在数据成员完成各自对齐之后,结构(或联合)本身也要进行对齐,对齐将按照#pragma pack指定的数值和结构(或联合)最大数据成员长度中,比较小的那个进行。
疑问:对于数据成员对齐规则:为什么每个成员的对齐都要按照Min(指定对齐模数,数据成员自身长度)来确定呢?为了不用Max(指定对齐模数,数据成员自身长度)呢,用Max值对齐的不更加完美么?同样对于结构的整体对齐规则也一样有此疑问。这里我们还是举个例子更加直观:
#pragma pack(8)
struct Foo {
char a;
int b;
short c;
};
#pragma pack()
我们先来看数据成员对齐,以b为例子,按照规则的说法,sizeof(b) = 4 < 8,那么Address_of_b = Start_Address_of_Foo + 4; 我们来看看当应用的代码里访问b的时候,CPU做了些什么?Address_of_b一半情况下是不能被8整除的,在不能被8整除的情况下,我们去访问b,这里我要提两个问题:
1) 访问b的时候是否会因内存没有对齐到8上而触发core呢?(在Sun SPARC上因访问未对齐地址上的变量时会出core)
2) 为什么不将b放到Start_Address_of_Foo + 8这个地址上呢?
下面一一说说我的理解:
根据前面所说,程序在访问b的时候,CPU实际不一定是从Address_of_b这个地址上开始读取的。如果b这个地址恰巧既能被4整除,也能被8整除(如地址24),那就无可厚非了。但是如果这个地址只能被4整除,而不能被8整除(如地址12),那么此时CPU读取的地址肯定是从Address_of_b - 4开始读取8个字节的,也就是说实际上CPU都是从能被8整除的地址上读取的,而且一次读了8个字节,b所在的位置恰是这个8个字节中的后4个字节,所以不存在触发core的可能。
第二个问题,sizeof(b) = 4 < 8,为什么就要按照4而不是按照8去安排b的地址呢?我们不妨按照8去给b分配地址,Address_of_b' = Start_Address_of_Foo + 8,这样的话CPU也能一次将b读取,而且是从b的起始地址开始读,似乎更完美。但你看出问题了么?这么做浪费的空间显然大了很多。将b安排在Address_of_b'比安排在Address_of_b多浪费了一半空间。
同样整体对齐原则也是同样的道理。内存对齐计算显然有两个目标:一是减少CPU的访存次数;第二个就是还要保持存储空间的效率足够高。
上文转自:http://blog.csdn.net/jiaocj223/article/details/6003243
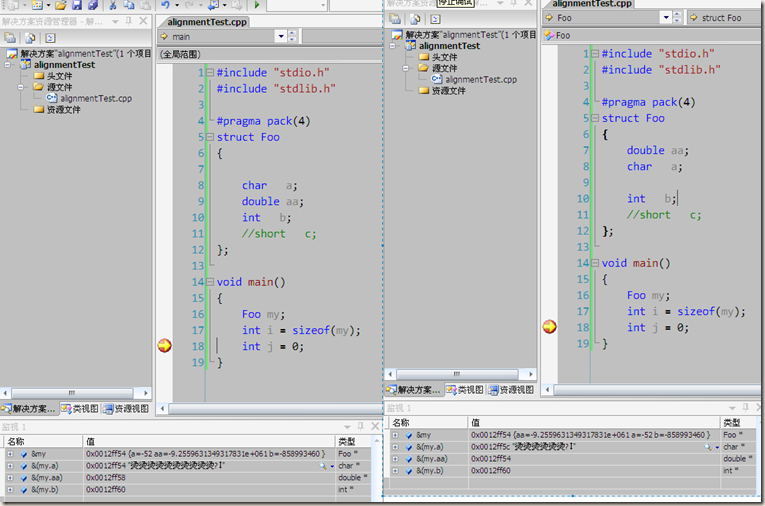
下面是自己碰到的两个具体的例子:
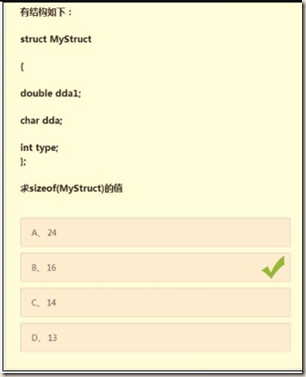
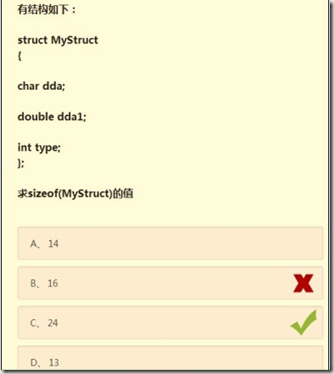
左图结构体大小为16字节,右图结构体大小为24字节。
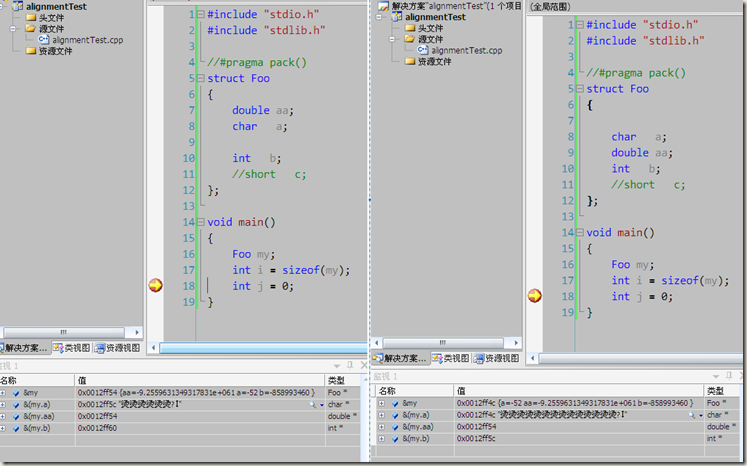
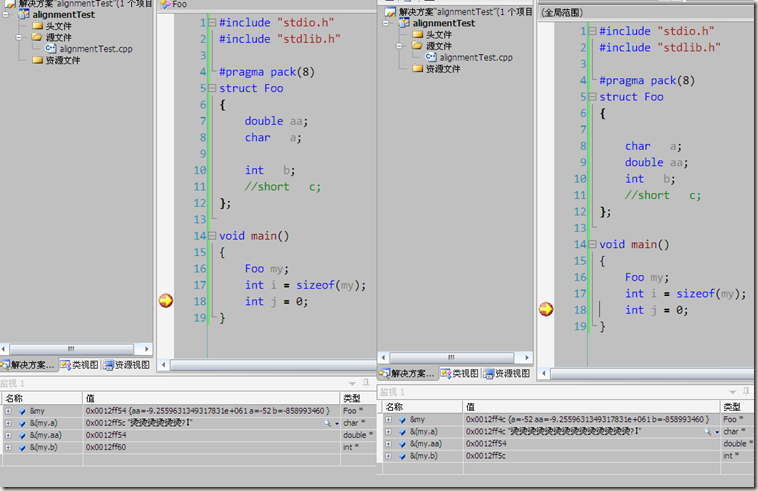
下面几张图是我自己在vs2005+winXP上做的实验:
验证了两个问题:1、vs2005默认是#pragma pack(8)的
2、符合上述分析。