最长公共子序列

题目

分析

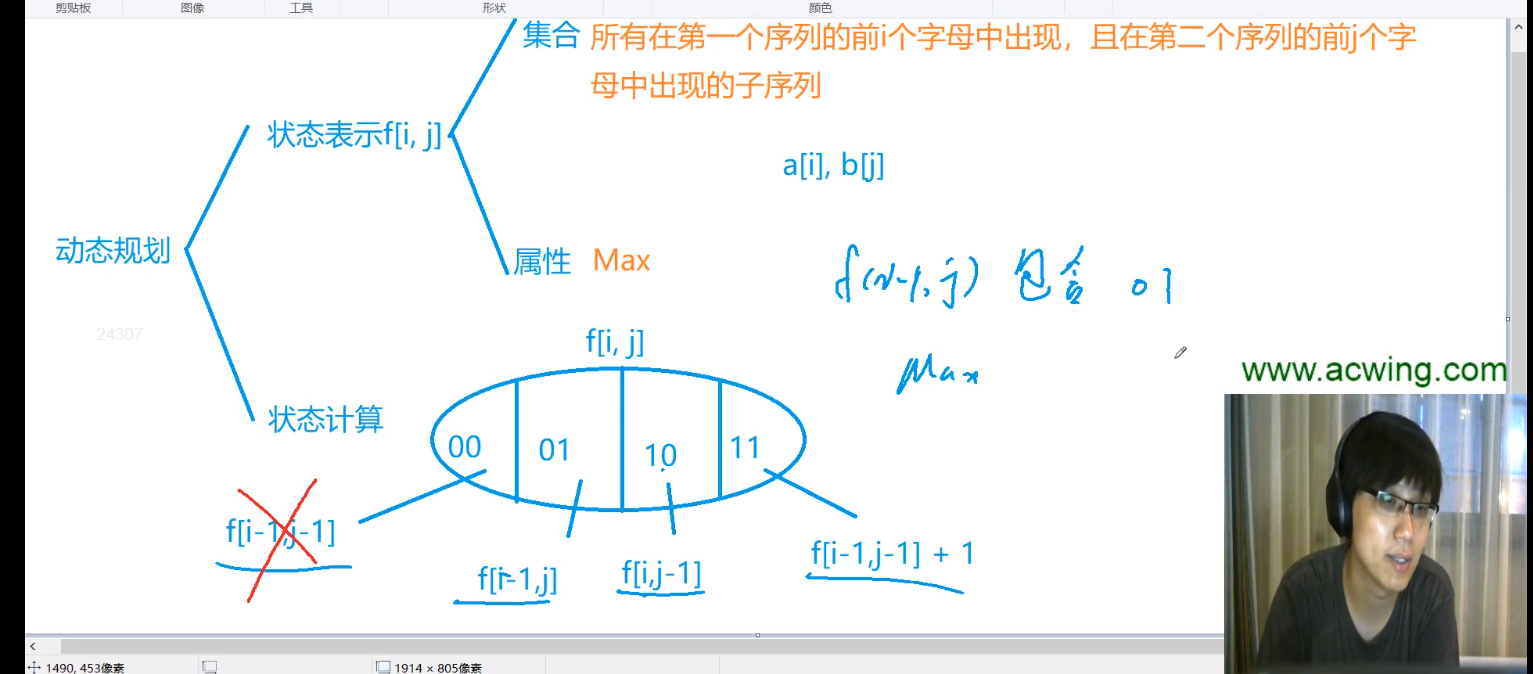
状态表示，这里有个技巧，题目涉及两个字符串我们一般采用二维dp数组（经验）。

 f(i,j)表示所有在第一个序列前 i 个字母中出现，且在第二个序列前 j 个字母出现的子序列的最长长度。重点是如何找递推公式。。。。

设第一个序列为a[]、第二个序列为b[]。f(i,j)所表示的最长子序列的构成：

1. 不含a[i] 不含b[j]

2. 不含a[i]，含b[j]  ≠  f(i-1,j)

3. 含a[i]  不含b[j]

4. 含a[i] 含b[j]

上面四种情况对应上图的00、01、10、11

说明：

1.上面分析的情况二不含a[i]，含b[j]，其实是f(i-1,j) 的子集。01的情况和f(i-1,j）表示的不是一个东西。 f(i-1,j表示的是在第一个序列前 i-1个字母出现且在第二个序列前 j 个字母出现的子序列的最大长度。这个子序列可以不含a[i-1]、不含 b[j-1]，可以含a[i-1] 、不含b[j]，可以不含a[i-1]、含b[j]，可以含a[i-1]、含b[j]。这四种情况。情况二01表示子序列不含 a[i] 含b[j] 。所以f(i-1,j)表示的范围要比01这种情况大。同理第三种情况10也是。

2.通过f(i-1,j)和f(i,j-1)就可以包含全部00、01、10这三种情况。所以通常我们会只考虑 f(i-1,j) 和 f(i,j-1）以及f(i-1,j-1) + 1。

还是不理解的话，试着从集合论的角度看，我们求的是最大值问题，不是排列组合问题，所以状态表示范围大于真实子集的划分没有关系，只要最终子状态的构成表示的全集即可，有重叠没关系。

求max可以重叠，求个数问题不可。

代码

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1010;
char a[N],b[N];
int dp[N][N];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    scanf("%s%s",a+1,b+1);
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            if(a[i] == b[j]) dp[i][j] = max(dp[i][j],dp[i-1][j-1]+1);
        }
    }
    printf("%d",dp[n][m]);
    return 0;
}

时间复杂度分析：状态数O(N²)，转移量O(1)（每次取三种情况最大值），所以时间复杂度为O(N²)

递推公式有i-1所以为了方便所有下标从1开始

1. scanf("%s%s",a+1,b+1);  +1是将字符串从a+1的位置开始保存，目的是为了下面递推公式判断一致，从1开始。

2. dp[i-1][j-1]+1 这种情况的出现有条件限制的