有问题的话欢迎在评论区提出
题意:
题目链接
你是一个送快递的,现在给你一个环,环的边有权值,代表走这条边所花的时间,每个点代表一个地点,点有点权,代表这个点上有多少货物需要你送。初始时间(t=0),每到一个点,你就可以瞬间送完该点所有的货物,但每一个货物都会给你带来值为当前时间的罚款。现在你要送完所有货物,问最优情况下你的罚款最少是多少。
题解:
从样例可以看出,这题的核心就在于,快递员可以“反复横跳”,比如可以先逆时针送完一个点的货物,再掉头沿顺时针方向送完所有其它点的货物(尽管这样使得一条边经过了两次,但使得总罚款更少了)。
为了方便下面的说明,先约定些定义:我把起点记做0号点,0号点逆时针走(j)格到达的点叫做“逆时针第(j)点”,0号点顺时针走(i)格到达的点叫做“顺时针第(i)点”;
例如,下图中,4号点是顺时针第4点与逆时针第2点。
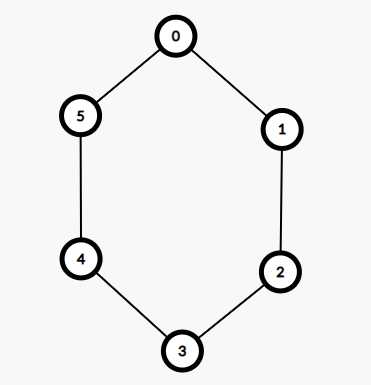
废话不多说,直接看状态的定义:
(dp[i][j][0]):如果(t=0)的时候你站在顺时针(i)号点,送完包括端点在内,整个([i,j])区间的最小罚款;
(dp[i][j][1]):如果(t=0)的时候你站在逆时针(j)号点,送完包括端点在内,整个([i,j])区间的最小罚款;
有两点值得注意的:
- 状态定义中假设了(t=0)时的位置,但事实上(t=0)的时候你是在起点的。为何这么假设呢?往下看就知道了;
- 上述所谓([i,j])区间,表示的是由i顺时针到j的区间(划重点,也就是说,该区间走的是不含起点的那条路!),这里为了便于理解说成是([i,j]),下面也用这种方式表示区间和点,不要搞混了。
那么仍以下图为例,取(i=1)和(j=1),看看如何更新;
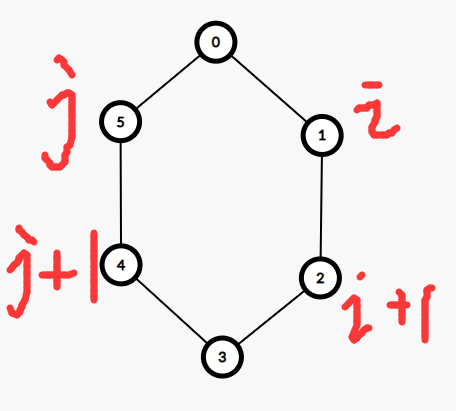
再次强调,该图里的([i,j])区间是(1,2,3,4,5)这一段
(dp[i][j][0])可以通过如下两种方式更新(特别提醒,由于(t=0)时你就在顺时针第(i)个位置,所以(i)处的货物不带来任何罚款,这也是下面两种情况中我们都无视了(i)点罚款的原因):
- 走到(i+1),这样做的花费是 : (dp[i+1][j][0]+)( 区间([i+1,j])的货物数量之和 (*i)与(i+1)点间的时间 )
解释:(dp[i][j][0])假设(t=0)的时候你在(i)处,而(dp[i+1][j][0])的(t=0)时刻假设你在(i+1)处,因此,两者的“开始时间”有个差距,即“(i)到(i+1)的时间”,该时间的影响是平均的作用在该区间所有货物上的。- 掉头走到(j),这样做的花费是 : (dp[i+1][j][1]+)( 区间([i+1,j])的货物数量之和 (*i)掉头走到(j)点的时间 )
解释:与上面的情况对比,仍然是([i+1,j])中的所有货物都统一的被拖延了一个时间,只不过这次该时间变成了(i)到(j)的一条路的时间
最终,(dp[i][j][0])的值就取这两者与自己之间的最小值,就可以完成更新。
(dp[i][j][1])的更新同理,可以参考下面dfs函数内写的方法。
后记:
最开始,我定义的(dp[i][j][0])是“由(i)逆时针到(j)全部送完的最小罚款”,也就是走含起点的那一条路,相信应该会有一些人第一反应也这么想吧。但这样搞的话,似乎就没法转移了,因为你没法处理掉头多次的情况。
总之,第一反应能想到一个正确的状态,真的很重要。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int inf=0x3f3f3f3f;
int n,num[310],len[310],lpre[310],npre[310];
int dp[310][310][2];
int nsum(int i,int j){
int tmp=(i!=0);j=n-j;
return npre[j]-npre[i-tmp];
}
int lsum(int i,int j){
return lpre[j]-lpre[i];
}
int dfs(int i,int j,int pos){
if(dp[i][j][pos]!=inf){
return dp[i][j][pos];
}
if(i+j>=n){
return dp[i][j][pos]=0;
}
if(pos==1){
dp[i][j][1]=min(dp[i][j][1],dfs(i,j+1,1)+len[n-(j+1)]*nsum(i,j+1));
dp[i][j][1]=min(dp[i][j][1],dfs(i,j+1,0)+(lpre[i]+lsum(n-j,n))*nsum(i,j+1));
}
else{
dp[i][j][0]=min(dp[i][j][0],dfs(i+1,j,0)+len[i]*nsum(i+1,j));
dp[i][j][0]=min(dp[i][j][0],dfs(i+1,j,1)+(lpre[i]+lsum(n-j,n))*nsum(i+1,j));
}
return dp[i][j][pos];
}
int main(){
while(~scanf("%d",&n)){
if(!n) break;
for(int i=0;i<n;i++){
scanf("%d%d",&num[i],&len[i]);
}
lpre[0]=npre[0]=num[n]=0;
for(int i=1;i<=n;i++){
lpre[i]=lpre[i-1]+len[i-1];
npre[i]=npre[i-1]+num[i];
}
memset(dp,inf,sizeof(dp));
int ans=min(dfs(0,0,0),dfs(0,0,1));
printf("%d
",ans);
}
return 0;
}