KMP算法
在介绍KMP算法之前,先介绍一下BF算法。
一.BF算法
BF算法是普通的模式匹配,BF算法的思想就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。
举例说明:
S: ababcababa
P: ababa
BF算法匹配的步骤如下:
i=0 i=1 i=2 i=3 i=4
第一趟:ababcababa 第二趟:ababcababa 第三趟:ababcababa 第四趟:ababcababa 第五趟:ababcababa
ababa ababa ababa ababa ababa
j=0 j=1 j=2 j=3 j=4(i和j回溯)
i=1 i=2 i=3 i=4 i=3
第六趟:ababcababa 第七趟:ababcababa 第八趟:ababcababa 第九趟:ababcababa 第十趟:ababcababa
ababa ababa ababa ababa ababa
j=0 j=0 j=1 j=2(i和j回溯) j=0
i=4 i=5 i=6 i=7 i=8
第十一趟:ababcababa 第十二趟:ababcababa 第十三趟:ababcababa 第十四趟:ababcababa 第十五趟:ababcababa
ababa ababa ababa ababa ababa
j=0 j=0 j=1 j=2 j=3
i=9
第十六趟:ababcababa
ababa
j=4(匹配成功)
代码实现:
int BFMatch(char *s,char *p)
{
int i,j;
i=0;
while(i<strlen(s))
{
j=0;
while(s[i]==p[j]&&j<strlen(p))
{
i++;
j++;
}
if(j==strlen(p))
return i-strlen(p);
i=i-j+1; //指针i回溯
}
return -1;
}
其实在上面的匹配过程中,有很多比较是多余的。在第五趟匹配失败的时候,在第六趟,i可以保持不变,j值为2。因为在前面匹配的过程中,对于串S,已知s0s1s2s3=p0p1p2p3,又因为p0!=p1!,所以第六趟的匹配是多余的。又由于p0==p2,p1==p3,所以第七趟和第八趟的匹配也是多余的。在KMP算法中就省略了这些多余的匹配。
二.KMP算法
KMP算法之所以叫做KMP算法是因为这个算法是由三个人共同提出来的,就取三个人名字的首字母作为该算法的名字。其实KMP算法与BF算法的区别就在于KMP算法巧妙的消除了指针i的回溯问题,只需确定下次匹配j的位置即可,使得问题的复杂度由O(mn)下降到O(m+n)。
前面提到,KMP算法通过一个"有用信息"可以知道目标串中下一个字符是否有必要被检测,这个"有用信息"就是用所谓的"前缀函数(一般数据结构书中的next函数)"来存储的。
这个函数能够反映出现失配情况时,系统应该跳过多少无用字符(也即模式串应该向右滑动多长距离)而进行下一次检测。
总的来讲,KMP算法有2个难点:
一是这个前缀函数的求法。
二是在得到前缀函数之后,怎么运用这个函数所反映的有效信息避免不必要的检测。
前缀函数的引入
对于前缀函数,先要理解前缀是什么:
简单地说,如字符串A = "abcde" B = "ab"
那么就称字符串B为A的前缀,记为B ⊏ A(注意那不是"包含于",Bill把它读作B前缀于A),说句题外话——"⊏"这个符号很形象嘛,封了口的这面相当于头,在头前面的就是前缀了。
同理可知 C = "e","de" 等都是 A 的后缀,以为C ⊐ A(Bill把它读作C后缀于A)
理解了什么是前、后缀,就来看看什么是前缀函数:
在这里不打算引用过多的理论来说明,直接引入实例会比较容易理解,看如下示例:

(下述字符若带下标,则对应于图中画圈字符)
这里模式串 P = "ababaca",在匹配了 q=5 个字符后失配,因此,下一步就是要考虑将P向右移多少位进行新的一轮匹配检测。传统模式中,直接将P右移1位,也就是将P的首字符'a'去和目标串的'b'字符进行检测,这明显是多余的。通过我们肉眼的观察,可以很简单的知道应该将模式串P右移到下图'a3'处再开始新一轮的检测,直接跳过肯定不匹配的字符'b',那么我们"肉眼"观察的这一结果怎么把它用语言表示出来呢?
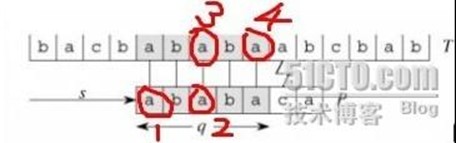
我们的观察过程是这样的:
P的前缀"ab"中'a' != 'b',又因该前缀已经匹配了T中对应的"ab",因此,该前缀的字符'a1'肯定不会和T中对应的字串"ab"中的'b'匹配,也就是将P向右滑动一个位移是无意义的。
接下来考察P的前缀"aba",发现该前缀自身的前缀'a1'与自身后缀'a2'相等,"a1 b a2" 已经匹配了T中的"a b a3",因此有 'a2' == 'a3', 故得到 'a1' == 'a3'......
利用此思想,可推知在已经匹配 q=5 个字符的情况下,将P向右移 当且仅当 2个位移时,才能满足既没有冗余(如把'a'去和'b'比较),又不会丢失(如把'a1' 直接与 'a4' 开始比较,则丢失了与'a3'的比较)。
而前缀函数就是这样一种函数,它决定了q与位移的一一对应关系,通过它就可以间接地求得位移s。
通过对各种模式串进行上述分析(大家可以自己多写几个模式串出来自己分析理解),发现给定一个匹配字符数 q ,则唯一对应一个有效位移,如上述q=5,则对应位移为2.
这就形成了一一对应关系,而这种唯一的关系就是由前缀函数决定的。
这到底是怎样的一种关系呢?
通过对诸多模式串实例的研究,我们会找到一个规律(规律的证明及引理详见《算法导论(第二版)》)。
上例中,P 已经匹配的字符串为"ababa",那么这个字符串中,满足既是自身真后缀(即不等于自身的后缀),又是自身最长前缀的字符串为"aba",我们设这个特殊字串的长度为L,显然,L = 3. 故我们要求的 s = q - L = 5 - 3 = 2 ,满足前述分析。
根据这个规律,即可得到我们要求的有效位移s,等于已经匹配的字符数 q 减去长度 L。
即 s = q - L
因为这个长度 L 与 q 一一对应,决定于q,因此用一函数来表达这一关系非常恰当,这就是所谓的前缀函数了。
因为已经分析得到该关系为一一对应关系,因此用数组来表示该函数是比较恰当的,以数组的下标表示已经匹配的字符数 q,以下标对应的数据存储 L。
前缀函数的实现
在KMP算法中,为了确定在匹配不成功时,下次匹配时j的位置,引入了next[]数组,next[j]的值表示P[0...j-1]中的真后缀的最长前缀的长度。
对于next[]数组的定义如下:
1) next[j] = -1 j = 0
2) next[j] = max(k): 0<k<j P[0...k-1]=P[j-k,j-1]
3) next[j] = 0 其他
如:
P a b a b a
j 0 1 2 3 4
next -1 0 0 1 2
即next[j]=k>0时,表示P[0...k-1]=P[j-k,j-1]
因此KMP算法的思想就是:
在匹配过程称,若发生不匹配的情况,
如果next[j]>=0,则目标串的指针i不变,将模式串的指针j移动到next[j]的位置继续进行匹配;
若next[j]=-1,则将i右移1位,并将j置0,继续进行比较。
代码实现:
int KMPMatch(char *s,char *p)
{
int next[100];
int i,j;
i=0;
j=0;
getNext(p,next);
while(i<strlen(s))
{
if(j==-1||s[i]==p[j])
{
i++;
j++;
}
else
{
j=next[j]; //消除了指针i的回溯
}
if(j==strlen(p))
return i-strlen(p);
}
return -1;
}
因此KMP算法的关键在于求算next[]数组的值,即求算模式串每个位置处的最长后缀与前缀相同的长度, 而求算next[]数组的值有两种思路,第一种思路是用递推的思想去求算,还有一种就是直接去求解。
1.按照递推的思想:
根据定义next[0]=-1,假设next[j]=k, 即P[0...k-1]==P[j-k,j-1]
1)若P[j]==P[k],则有P[0..k]==P[j-k,j],很显然,next[j+1]=next[j]+1=k+1;
2)若P[j]!=P[k],则可以把其看做模式匹配的问题,即匹配失败的时候,k值如何移动,显然k=next[k]。
因此可以这样去实现:
void getNext(char *p,int *next)
{
int j,k;
next[0]=-1;
j=0;
k=-1;
while(j<strlen(p)-1)
{
if(k==-1||p[j]==p[k]) //匹配的情况下,p[j]==p[k]
{
j++;
k++;
next[j]=k;
}
else //p[j]!=p[k]
k=next[k];
}
}
2.直接求解方法
void getNext(char *p,int *next)
{
int i,j,temp;
for(i=0;i<strlen(p);i++)
{
if(i==0)
{
next[i]=-1; //next[0]=-1
}
else if(i==1)
{
next[i]=0; //next[1]=0
}
else
{
temp=i-1;
for(j=temp;j>0;j--)
{
if(equals(p,i,j))
{
next[i]=j; //找到最大的k值
break;
}
}
if(j==0)
next[i]=0;
}
}
}
bool equals(char *p,int i,int j) //判断p[0...j-1]与p[i-j...i-1]是否相等
{
int k=0;
int s=i-j;
for(;k<=j-1&&s<=i-1;k++,s++)
{
if(p[k]!=p[s])
return false;
}
return true;
}
KMP算法实现(《算法导论》上的思路)&&ACM练习题
HDOJ 2087(http://acm.hdu.edu.cn/showproblem.php?pid=2087)
//HDOJ 2087 (http://acm.hdu.edu.cn/showproblem.php?pid=2087)
//KMP算法的应用(依据算法导论上的思路)
#include <iostream>
#include <cstdio>
#include <string>
using namespace std;
const int MAX_LEN = 1005;
//前缀函数
int prefix_function[MAX_LEN];
//函数:
//功能:计算模式字符串的前缀函数
void compute_prefix_function(char *p);
//函数:
//功能:KMP匹配算法
int kmp_match(char *T,char *P);
int main(){
char str1[MAX_LEN],str2[MAX_LEN];
while(scanf("%s",&str1)){
if ('#' == str1[0])
{
break;
}
scanf("%s",&str2);
compute_prefix_function(str2);
int count = kmp_match(str1,str2);
cout << count << endl;
}
return 0;
}
//需要注意的是,字符串下表从0开始
int kmp_match(char *T,char *P){
int len1 = strlen(T);
int len2 = strlen(P);
//记录已经匹配到的字符数
int q = 0;
//记录模式字符串出现的次数
int count = 0;
for (int i = 0;i < len1;++i)
{
//如果前一次匹配已经匹配了大于0的字符数,而下一个字符不匹配,
//那么下次匹配的时候跳过前缀字符串,避免冗余的回溯
while(q > 0 && P[q] != T[i])
q = prefix_function[q];
//下一个字符也匹配,已经匹配到的字符数加一
if (P[q] == T[i])
++q;
//已经匹配到的字符数等于模式字符串的长度
if (q == len2)
{
//输出模式字符串在要匹配的字符序列中索引
++count;
//寻找下一个匹配
//q = prefix_function[q];
q = 0;
}
}
return count;
}
void compute_prefix_function(char *p){
//初始化
prefix_function[1] = 0;
int len = strlen(p);
int k = 0;//记录已经匹配的字符的个数
for (int i = 1;i < len;++i)
{
//如果前面当前已经匹配的字符数目是k,下一个字符不匹配,
//下一次搜索的时候从prefix_function[k]处开始匹配,而不是从开始
while(k > 0 && p[k + 1] != p[i])
k = prefix_function[k];
//下一个字符也匹配,则前缀函数值相比前面的加一
if (p[k] == p[i])
++k;
//前缀函数赋值
prefix_function[i + 1] = k;
}
}
参考资料
http://www.cnblogs.com/dolphin0520/archive/2011/08/24/2151846.html
http://billhoo.blog.51cto.com/2337751/411486
附件: