AcWing 带分数 dfs

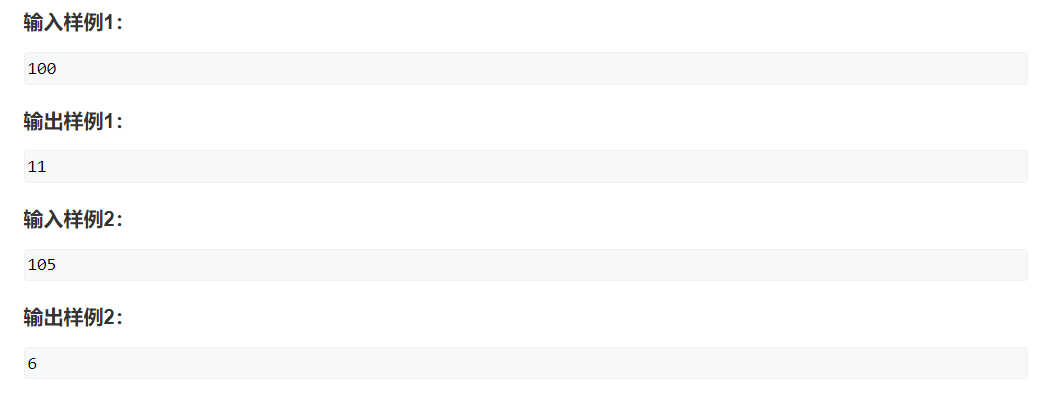
方法一：

最原始，最暴力，耗时4秒，但是是最好想的思路。

生成1~9的全排列。对于每个全排列，依次枚举a，b，c的位数。枚举三个数的位数时，就相当于在9个数形成的8个空里，插入俩隔板。

所以时间复杂度大致是全排列个数9！乘以8个空里选俩的组合数：c（8，2）。

估计是10,160,640。不过按电脑1秒计算量是10^7看的话，运行4秒大致时间复杂度是4*10^7左右。‬

能得出正确答案，不过绝对会超时。

#include <bits/stdc++.h>
using namespace std;
int n, ans;
int a[9] = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int getNum(int l, int r) { //求出这个数
    int res = 0;
    for (int i = l; i <= r; i++) {
        res = res * 10 + a[i];
    }
    return res;
}
bool check(int a, int b, int c) { //判断n == a + b / c
    if (b % c != 0) {
        return false;
    }
    if (a + b / c != n) {
        return false;
    }
    return true;
}
int main() {
    cin >> n;
    do {
        for (int i = 0; i <= 6; i++) { 
            for (int j = i + 1; j <= 7; j++) { // c必须大于0，所以要给c留出一位
                int a = getNum(0, i);
                int b = getNum(i + 1, j);
                int c = getNum(j + 1, 8);
                if (check(a, b, c)) {
                    ans++;
                }
            }
        }
    } while (next_permutation(a, a + 9));
    cout << ans << endl;
    return 0;
}

方法二：

优化版。1.2秒左右，按理说还是会超时，不过是目前为止的最优解。

方法一中是直接枚举a，b，c的位数，自变量是三个，没有用到题目给出的性质。

方法二把等式n = a + b / c两边乘上c，得c * n = c * a + b。

n是给出的，枚举a和c就好，b可以直接算出，自变量是两个了。

n最多只有7位。

搜索思路：

　　先枚举a，对于每个枚举的a再枚举c，最后再判断等式是否成立。就是递归搜索a时在每一个递归搜索树的叶子节点后再接上另一个递归搜索树用来递归搜索c，然后在这个树的叶子节点上判断一下等式是否成立。

#include <bits/stdc++.h>
using namespace std;
const int N = 20; 
typedef long long ll;
int n;
int ans;
bool st[N], bk[N]; //判重数组和备份数组 
bool check(int a, int c) { //判断a和c是不是满足要求
     ll b = (ll)c * n - (ll)c * a; 
     if (!a || !b || !c) { //a,b,c不能为0 
         return false;
     }
     memcpy(bk, st, sizeof st); //把st复制给bk
     while (b) { //拆出b的每一位 
         int x = b % 10;
        b /= 10;
        if (!x || bk[x]) { //如果x为0或者x已经出现过，就不合法 
            return false;
        }
        bk[x] = true;
     } 
     for (int i = 1; i <= 9; i++) { //判断9个数是不是全都出现过 
         if (!bk[i]) { 
             return false;
         }
     }
     return true;
}
void dfs_c(int u, int a, int c) {
    if (u == n) { //如果已经用完了n个数字 
        return;
    }
    if (check(a, c)) {
        ans++;
    } 
    for (int i = 1; i <= 9; i++) {
        if (!st[i]) {
            st[i] = true;
            dfs_c(u + 1, a, c * 10 + i);
            st[i] = false;
        }
    }
} 
void dfs_a(int u, int a) { //参数一：u表示已经用了多少个数字， 参数二：表示a的值 
    if (a >= n) { //a,b,c三个数字至少有一位 
        return;
    }
    //对于a<n的每种方案，枚举c 
    if (a) {
        dfs_c(u, a, 0); //u个数了，a的值为a，c的值为0 
    }
    //枚举当前这一位可以用哪个数字
    for (int i = 1; i <= 9; i++) {
        if (!st[i]) {
            st[i] = true;
            dfs_a(u + 1, a * 10 + i);
            st[i] = false; //回溯恢复现场 
        }
    } 
}
int main() {
    cin >> n;
    dfs_a(0, 0); //一个数都没有， a = 0 
    cout << ans << endl; 
    return 0;
}