
这道题目其实我也不会,第一次学习只是有个模糊的框架
之后还需要复习
需要配合一丢丢图论的基础知识,涉及到的不多
暴力做法时间复杂度就是阶乘级别的
依然是用状态压缩DP
用一个整数表示一个状态
每个点只能走一次
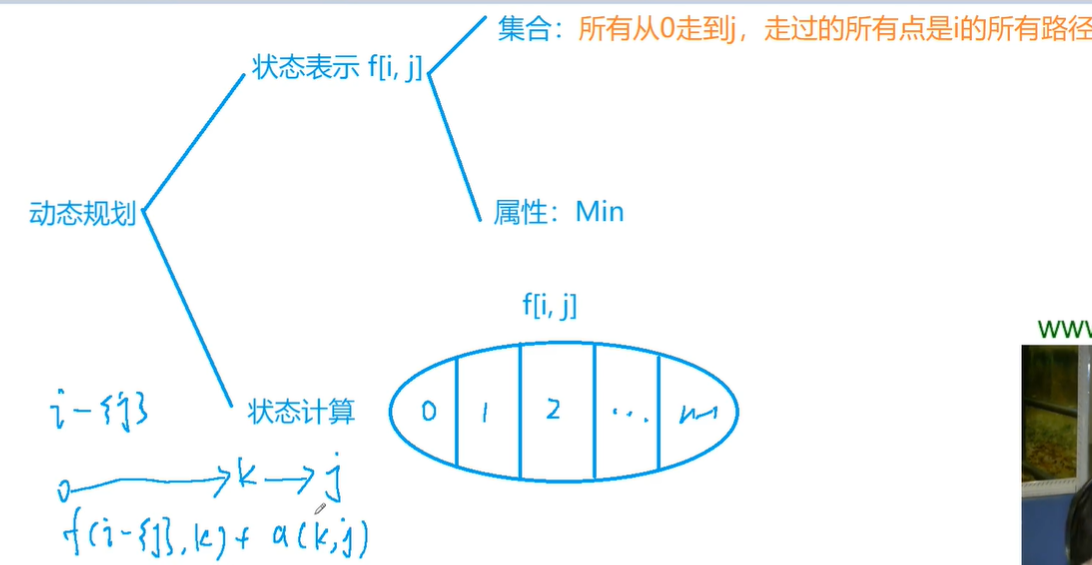
dp[i][j]中的i就是压缩后的一个状态
i这个二进制数中的每一位分别表示当前这个点是否走过了
比如说i = 1110011时
从右到左看,就表示
0号点已经走过了
1号点已经走过了
2号点没有走过
3号点没有走过
4号点已经走过了
5号点已经走过了
6号点已经走过了
集合划分:根据倒数第二个点是哪个点来分类
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 21, M = (1 << N); 4 int w[N][N]; //两点之间的距离 5 int dp[M][N]; 6 int main() { 7 int n; 8 cin >> n; 9 for (int i = 0; i < n; i++) { 10 for (int j = 0; j < n; j++) { 11 cin >> w[i][j]; 12 } 13 } 14 memset(dp, 0x3f, sizeof dp); //求最小值要初始化为一个较大值 15 dp[1][0] = 0; //边界值 16 for (int i = 0; i < (1 << n); i++) { //所有状态 17 for (int j = 0; j < n; j++) { //所有点 18 if (i >> j & 1) { 19 for (int k = 0; k < n; k++) { //枚举下从哪个点转移过来 20 if (i - (1 << j) >> k & 1) { //从k点转移过来 21 dp[i][j] = min(dp[i][j], dp[i - (1 << j)][k] + w[k][j]); 22 } 23 } 24 } 25 } 26 } 27 cout << dp[(1 << n) - 1][n - 1] << endl; 28 return 0; 29 }