-
Hoeffding不等式
本篇文章不详细证明霍夫丁不等式怎么来的,主要讨论如何由霍夫丁不等式证明不等式:
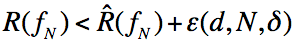
左端即为泛化误差,右端则为泛化误差上界。泛化误差也可以理解为期望风险,而右式第一个也叫做经验风险。
这都是与我们的的模型相关的,我们希望我们的模型对未知数据也能有好的预测能力,也就是泛化能力较强,这样才能说明我们的模型有着一定的可用性。
证明上式则需要我们的霍夫丁不等式:
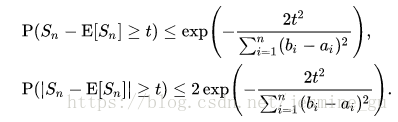
-
泛化误差上界推导
这里我们给出详细推导过程,并给每一步相应解释。
如果针对二分类问题,此时误差函数取值只为 1或0 ,此时对于一组独立同分布变量X1,X2,X3…Xn。则Xi等于0或1。
即对所有的i,有[ai,bi]=[0,1]。设F为X道Y的假设空间,此时若函数f属于该假设空间,则有:
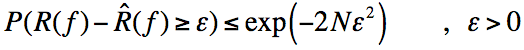
R(f)即为期望风险,^R(f)即为经验风险,关于经验风险或期望风险有不是很了解的可以看看我之前的博客。推导过程如下由霍夫丁不等式有:

对于上式,先是将t替换再是利用bi-ai=1。得到上式。且我们可知R(f)=Sn/n),^R(f)=ESn/n。
则可得下式
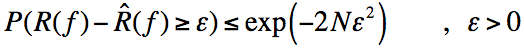
此时又有:

这里f属于假设空间的函数,但该假设空间是有限集合。第一个式子表示假设空间中函数满足上泛化误差上界公式的概率。此时它应等于每个函数满足泛化误差公式的概率的并集,这里可以将概率看成面积去理解,若每个函数都没有相交部分,则二式与三式相等,若有重合部分,则二式小于三式,这也就是二式小于等于三式的由来。再由霍夫丁不等式,则可得到四式。
此时则可有
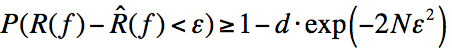
令