[算法]用java实现堆操作

问题描述：
(1)建堆：将数组A[1..n]变成一个最大堆。(课本6.3)
(2)堆排序：将一个堆中的元素按递减排序输出。
(3)用插入方法建堆：堆大小从1到n每次插入一个元素到堆中，直到n个元素入堆。(课本p83，6-1)

public class heap_Tools {
    //将一个元素插入堆中
    public static void insert(List<Integer> heap,int value){
        if(heap.size() == 0){     //0下标放置null
            heap.add(0, null);
            heap.add(1,value);
        }else {
            heap.add(value);
            heapUp(heap,heap.size()-1);
        }
    }
    //插入后向上调整位置，转变为大顶堆
    public static void heapUp(List<Integer> heap,int index){
        if(index >1){
            int parent = index/2;
            if(heap.get(parent) < heap.get(index)){
                swap(heap, parent, index);
                heapUp(heap, parent);
            }
        }
    }
    //对大顶堆排序
    public static List<Integer> sort(List<Integer> heap){
        for(int i = heap.size()-1;i>0;i--){
            swap(heap, 1,i );
            adjust(heap, 1, i-1);;
        }
        return heap;
    }
    //生成并输出一个大顶堆
    public static List<Integer> adjust(List<Integer> heap){
        for(int i =heap.size()/2;i>0;i--){
            adjust(heap,i,heap.size()-1);
        }
        System.out.println("将数组转化为最大堆输出:");
        print_heap(heap);
        return heap;
    }
    public static void adjust(List<Integer> heap,int index,int n){
        int child = index*2;
        if((child+1)<=n&&heap.get(child)<heap.get(child+1)){  //判断如果左孩子<右孩子
            child +=1;
        }
        if(child<n&&heap.get(index)<heap.get(child)){
            swap(heap,index,child);
        }
        if(child<=n/2){
            adjust(heap, child, n);  //交换后，以child为根的子树不一定满足大顶堆定义，递推调整
        }
    }
    //交换List中的两个值
    public static void swap(List<Integer> heap,int a,int b) {
        int temp;
        temp = heap.get(a);
        heap.set(a, heap.get(b));
        heap.set(b, temp);
    }
    public static void print_heap(List<Integer> heap){
        int floors = 0;
        for(int i = 1;i<heap.size();i++){
            System.out.print(heap.get(i)+"	");
            if(i == (2<<floors)-1){
                floors++;
                System.out.print("
");
            }
        }
    }
}

二：下沉法获得最大堆

public class Max_heap {

    public static void main(String[] args){
        //下沉法获得最大堆
        int[] A =  {1,2,5,10,3,7,11,15,17,20,10,9,5,8,6};
        List<Integer> array = new ArrayList<Integer>();
        array.add(0, null);
        for(int i = 0; i<A.length;i++){
            array.add(A[i]);
        }
        heap_Tools.adjust(array);
    }
}

三：将堆按照从大到小输出

public class heap_sort {
    public static void main(String[] args){
        //下沉法获得最大堆
        int[] A =  {1,2,5,10,3,7,11,15,17,20,10,9,5,8,6};
        List<Integer> array = new ArrayList<Integer>();
        array.add(0, null);
        for(int i = 0; i<A.length;i++){
            array.add(A[i]);
        }
        List<Integer> heap = heap_Tools.adjust(array);
        heap = heap_Tools.sort(heap);
        System.out.println("将堆中元素按递减顺序输出:");
        for(int i = heap.size()-1;i>0;i--){
            System.out.print(heap.get(i)+"	");
        }
    }
}

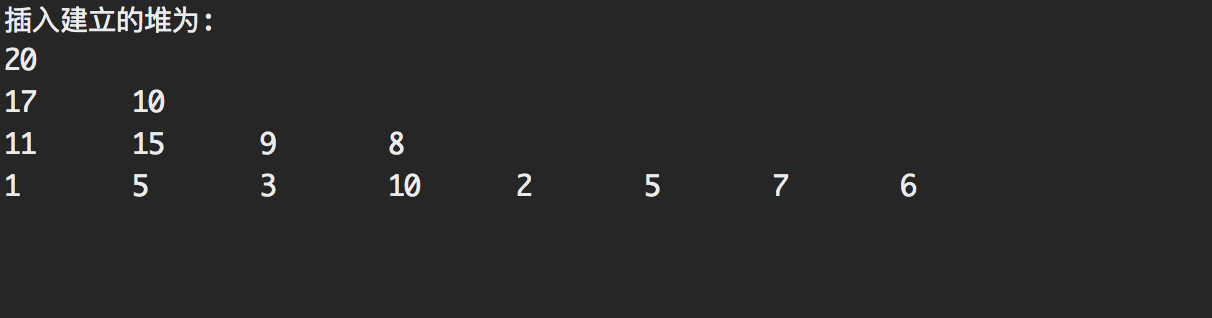
四：插入法建堆

public class insert_build_heap {
    public static void main(String[] args){
        //下沉法获得最大堆
        int[] A =  {1,2,5,10,3,7,11,15,17,20,10,9,5,8,6};
        List<Integer> array = new ArrayList<Integer>();
        for(int i = 0; i<A.length;i++){
            heap_Tools.insert(array,A[i]);
        }        
        System.out.println("插入建立的堆为:");
        heap_Tools.print_heap(array);
    }
}