递归
一棵树要么是空树,要么有两个指针,每个指针指向一棵树。树是一种递归结构,很多树的问题可以使用递归来处理。
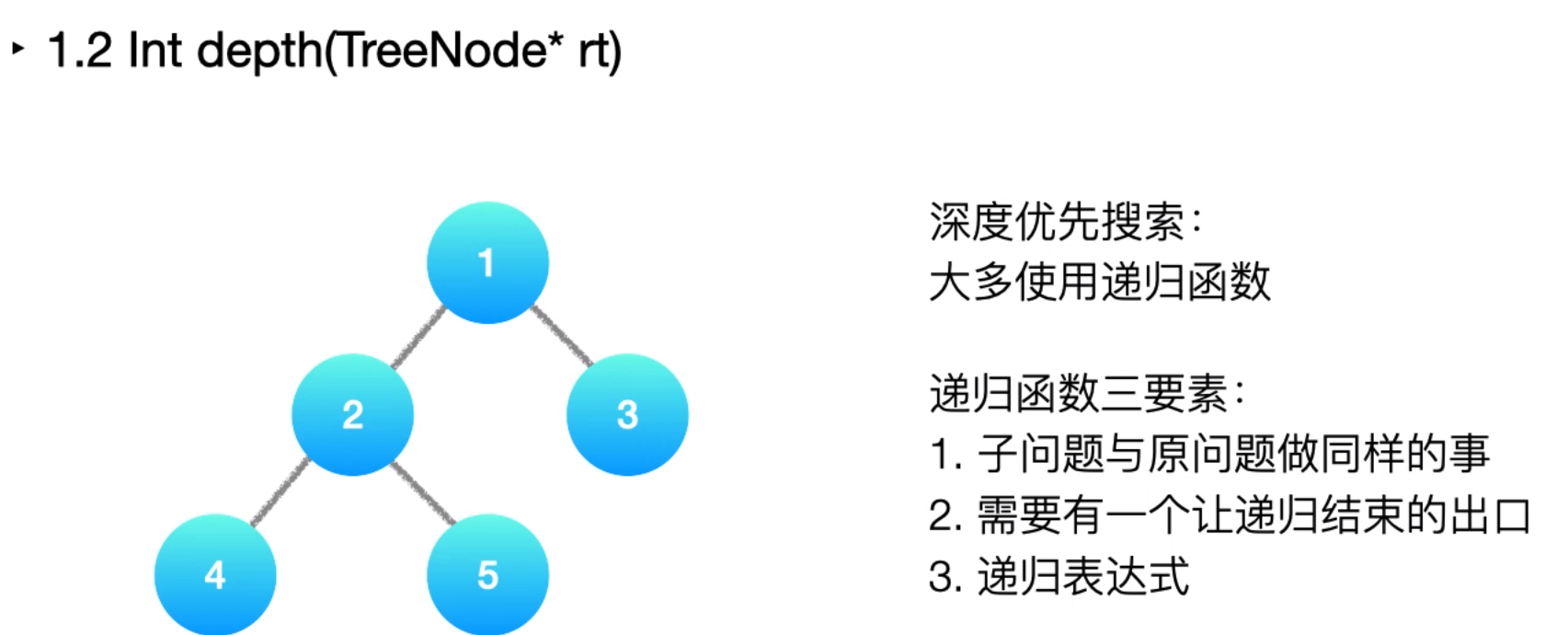
1. 树的高度
104. Maximum Depth of Binary Tree (Easy)
传入的TteeNode root 结点有左结点left右结点right两个属性,是跟root一样的TreeNode。所以是递归结构。二叉链表的存储结构。
该题的递归过程分析在第3题。现在是懂了,看到再分析一下看是不是真的记住了。
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public int maxDepth(TreeNode root) { if(root==null){ return 0; } return Math.max(maxDepth(root.left),maxDepth(root.right))+1;//返回求深度,DFS。找左儿子和右儿子的深度最大的那个加1 } }
2. 平衡树
110. Balanced Binary Tree (Easy)
3
/
9 20
/
15 7
平衡树左右子树高度差都小于等于 1
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { boolean result = true;//定义一个为ture的全局变量 可是很难想到1002 public boolean isBalanced(TreeNode root) { maxDepth(root); return result; } public int maxDepth(TreeNode root){ if(root==null) return 0; if((Math.abs(maxDepth(root.left) - maxDepth(root.right))) > 1){//没有这一步的话 前面就直接返回事先定好的true。
意思是树上任意节点左右子树深度若差值大于1了的话,把全局变量在这里改成了一个false.但不影响求树的最大深度!! result = false; } return Math.max(maxDepth(root.left),maxDepth(root.right))+1;//返回的依然是树的最大深度。但重要的是if条件判断 } }
主判断方法为isBalanced(),其中调用了maxDepth()
maxDepth()方法中,我们通过递归,计算了每个节点的左右子树的深度并进行比较,若差距大于1,则将result置为false(不平衡)
这一题比上一题这个判断
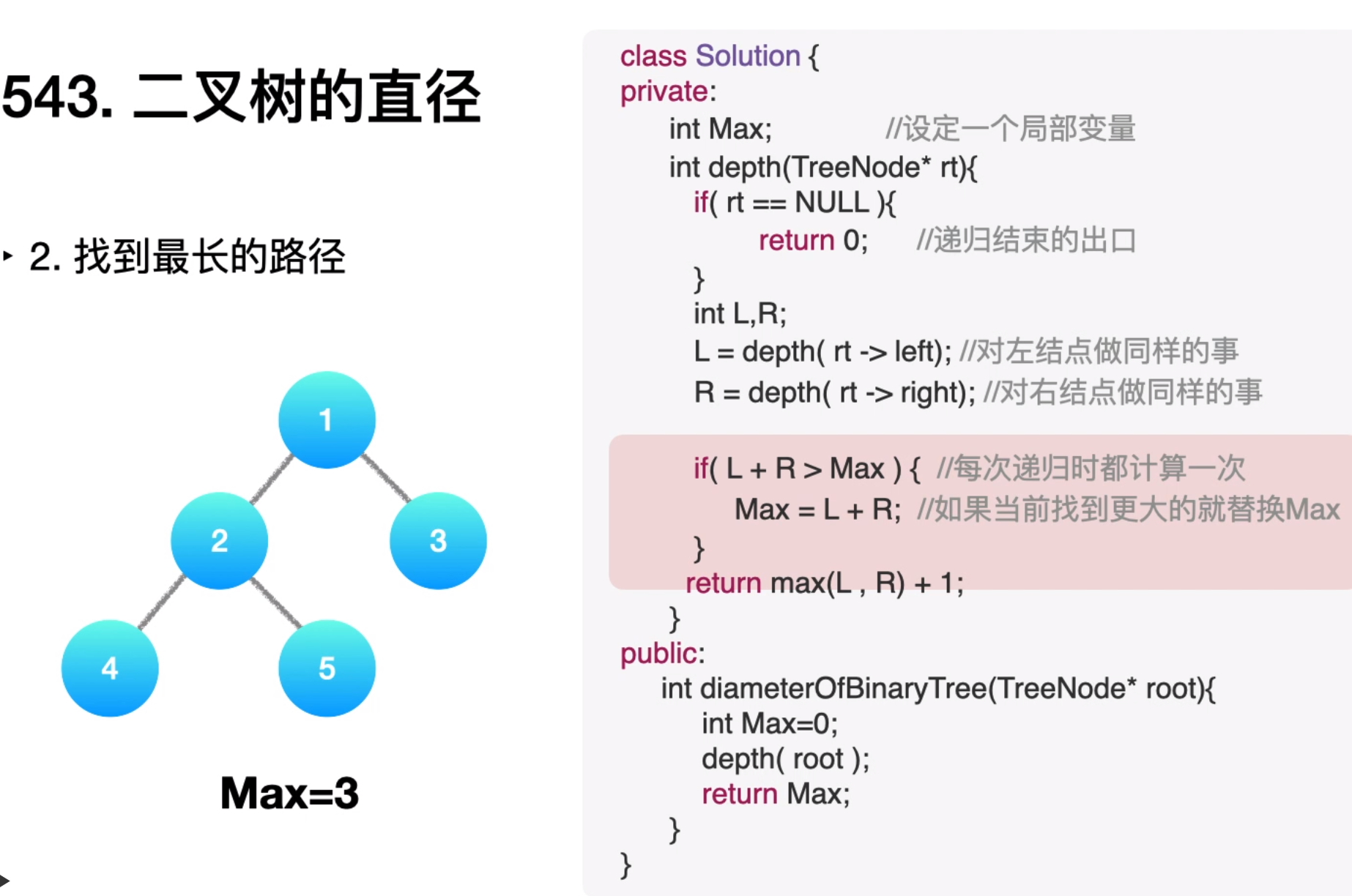
3. 两节点的最长直径
543. Diameter of Binary Tree (Easy)
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
Input:
1
/
2 3
/
4 5
Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
都没有思路,希望第二次做时可以有思路
答案解析:

又是换一种方式用递归计算深度,然后这次需要两边最大的深度加起来就是最长路径
 递归出口很重要
递归出口很重要
这一题总结下两题的求深度(深度优先搜索):


这个第一题的递归过程是1的左儿子2先进入这一行里的递归方法,执行方法回到第一行,看2是否为空,不为空往下走,找到左儿子4继续这个方法,又从第一行从上往下,先看4是否为空,不为空往下走,找4的左儿子执行方法,为空了此时,retrun 0出了这一行递归,L=0。继续往下一行代码走。
又进入递归方法,此时rt还是4,找4的右儿子(后1/2)从递归方法第一行执行,为空了此时,retrun 0出了这一行递归,R=0。
4的前1/2和后1/2都完成了。。。。
然后往下走 return max(0,0)+1 =1 返回的是4的深度
然后得返回上一层到2的右儿子(后1/2...) 好突然
找到右儿子5,又进入递归方法第一行,由于是空 return 0 。找5的右儿子,又进入递归方法第一行,由于是空return 0...
5的完成,往下走return 1返回的是5的深度
2也前后都完成了,往下走return max(1,1)+1 =2 返回的是2的深度 好突然
就是每一个结点得左右儿子完成,return出一个数,才返回上一层。
返回到1的右儿子3执行递归方法,左儿子空=0,右儿子空=0,return max(0,0)+1 =1是3的深度
然后1的深度就是max(2,1)+1=3
总结过程就是遇到递归方法参数进去,返回到递归方法第一行,一直执行到递归出口,此时的最底层执行下一个语句,若又是递归则又到第一行往下执行,若遇到递归出口,则可以该层完成后1/2,返回上一层完成递归后半段1/2整体完成直到递归出口。(走一遍就明白了)。关于什么时候用,应该是遇到传入的数据结构是一种递归结构去实现某个方法时,(链表好像也可以? 或者像阶乘这种方法
然后我们通过左右遍历返回有可能就认识这个3就是答案,这在上图是对的,但是在下图就不对了。
如果是下图,按上面从1出发的思路找到3条,就不对了。最多应该是不经过1的4条。

注意可能并不穿过根节点,这里主方法中的Max=depth(root.left)+depth(root.right)是只取经过主节点的左加右长度!!!
改掉这个代码,不用Max只等于root的左加右,改成Max--任意节点的左加右存住最大的那个返回Max给主方法。
这个改的过程有点难理解,但是结合刚刚递归的过程,加上如上图这种情况分析递归,当从5后1/2的完成返回到2这里的时候,2的后1/2完成,此时L是4返回的2,R是5返回的2,L+R=4,Max存住了。就算再返回到1,1的后1/2返回的R=0,L为2返回的3,L+R =3 其实小于2的左右相为4.
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { int max=0; public int diameterOfBinaryTree(TreeNode root) { deepth(root); return max; }
public int deepth(TreeNode root){ if(root==null){ return 0; } int L,R; L=deepth(root.left);//左子的深度 R=deepth(root.right);//右子的深度 max=Math.max(L+R,max);//某个节点为头结点时,此时更新的最大的左子加右子的深度,是最长的路径 return Math.max(L,R)+1;//这是节点的深度的计算。但是我们重要的是return的max。上一题也是 } }
4. 翻转树
226. Invert Binary Tree (Easy)
思路:
public TreeNode invertTree(TreeNode root) { if(root==null){ return null; } invertTree(root.left); invertTree(root.right); root.left=root.right;//错了。。。。。 return root; }
思路是对的,交换语句写错了!!这是赋值。。不是交换。。。
class Solution { public TreeNode invertTree(TreeNode root) { if(root==null){ return null; } invertTree(root.left); invertTree(root.right); TreeNode temp; temp=root.right; root.right=root.left; root.left=temp; return root; } }
5. 归并两棵树
617. Merge Two Binary Trees (Easy)
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
Input:
Tree 1 Tree 2
1 2
/ /
3 2 1 3
/
5 4 7
Output:
3
/
4 5
/
5 4 7
思路是列出三种情况,然后递归相加。怎么写val想加呢?
错误之处:
1.应该是先相加,再递归。(前序遍历就是这样,先打印值,再判断有没有左,有左就进入递归,再判断有没有右,有右再进入递归。)
2.相加的结果直接用构造方法new出结果结点传入值作为参数即可。
3.左右递归的结果分别要做为结果结点的左子树和右子树。
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; }//构造方法new一个就是 * } */ class Solution { public TreeNode mergeTrees(TreeNode t1, TreeNode t2) { if(t1==null && t2==null) return null; if(t1==null) return t2; if(t2==null) return t1; TreeNode root = new TreeNode(t1.val+t2.val); root.left= mergeTrees(t1.left,t2.left); root.right=mergeTrees(t1.right,t2.right); return root; } }
6. 判断路径和是否等于一个数
Leetcdoe : 112. Path Sum (Easy)
Given the below binary tree and sum = 22,
5
/
4 8
/ /
11 13 4
/
7 2 1
return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.
路径和定义为从 root 到 leaf 的所有节点的和。
emmm没有想法。。
答案:
最直接的方法就是利用递归,遍历整棵树:如果当前节点不是叶子,对它的所有孩子节点,递归调用 hasPathSum 函数,其中 sum 值减去当前节点的权值;如果当前节点是叶子,检查 sum 值是否为 0,也就是是否找到了给定的目标和。
(和是摊到每个节点的,所以一路减下来到叶子结点的值就是叶子结点的值)
class Solution { public boolean hasPathSum(TreeNode root, int sum) { if (root == null) return false; sum -= root.val; if ((root.left == null) && (root.right == null))//一般是判断节点为空 但这里需要判断是否是叶子 没到下一步 return (sum == 0);//到达了叶子,判断是否达到了目标值。=0则说明加上这个叶子值达到了目标
return hasPathSum(root.left, sum) || hasPathSum(root.right, sum);//可以分开看 只要左右有一个达到为==0为ture就行 } }
这题有点难想到。但愿下次会做了。。emmmm1003还是不会
7. 统计路径和等于一个数的路径数量
437. Path Sum III (Easy)
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/
5 -3
/
3 2 11
/
3 -2 1
Return 3. The paths that sum to 8 are:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
路径不一定以 root 开头,也不一定以 leaf 结尾,但是必须连续。
思路是第三题也不是必须经过root,在中间加一个存住满足的树。(应该是想到让其他节点为头结点时
class Solution { public int pathSum(TreeNode root, int sum) { if(root == null){ return 0; } int count=0; sum-=root.val; int left = pathSum(root.left,sum); int right = pathSum(root.right,sum-left);//错的!! if(left+right == sum){ count++; } return count; } }
错了。。int right明显就不对。
答案:
题目要求 路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点) 。这就要求我们只需要去求三部分即可:
以当前节点作为头结点的等于sum路径数量
以当前节点的左孩子作为头结点的等于sum路径数量
以当前节点的右孩子作为头结点的等于sum路径数量
将这三部分之和作为最后结果即可。1003:其实也是递归
最后的问题是:我们应该如何去求以当前节点作为头结点的路径的数量?这里依旧是按照树的遍历方式模板,每到一个节点让sum-root.val,并判断sum是否为0,如果为零的话,则找到满足条件的一条路径。
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public int pathSum(TreeNode root, int sum) { if(root == null) return 0; //当前节点开始的所有满足条件的路径总数 int result = countPath(root,sum); //当前节点左子节点开始的满足条件路径总数 int a = pathSum(root.left,sum); //当前节点右子节点开始的满足条件路径总数 int b = pathSum(root.right,sum); return result+a+b; } public int countPath(TreeNode root,int sum){//这个方法是传入作为头结点时,计算等于sum的路径数 if(root == null) return 0; sum = sum - root.val; int result = sum == 0 ? 1:0;//result计数 //当前节点开始的所有满足条件的路径总数分为左,右两条路径
}
}
不知道什么时候需要分开另外写方法。。第三题也另外写了方法。。
8. 子树
572. Subtree of Another Tree (Easy)
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
Given tree s:
3
/
4 5
/
1 2
Given tree t:
4
/
1 2
Return true, because t has the same structure and node values with a subtree of s.
Given tree s:
3
/
4 5
/
1 2
/
0
Given tree t:
4
/
1 2
Return false.
思路:可以像上一题一样,
class Solution { public boolean isSubtree(TreeNode s, TreeNode t) { if(s==null||t==null){ return false; } return (sub(s,t)||isSubtree(s.left,t)||isSubtree(s.right,t)); } public boolean sub(TreeNode s,TreeNode t){ if(s==null||t==null){ return false; } if(s==t){//错了 这是内存地址判断了。。。应该用值判断 但思路是对的 判断头或左子或右子 有一个是就是 return true; } sub(s.left,t); sub(s.right,t); return true; } }

错了。。。。。。。啥都return true了。。。
最下面一行改成
return sub(s.left,t)||sub(s.right,t);
又错了。。。变成啥都return false了。。。

看答案,首先第一行就错了,应该是
if (t == null) return true; // t 为 null 一定都是 true if (s == null) return false; // 这里 t 一定不为 null, 只要 s 为 null,肯定是 false
然后看s和t是否一样不能用s==t....要用值判断。。。。我这么这么二居然直接用== 这是存的地址。。。
答案:
class Solution { public boolean isSubtree(TreeNode s, TreeNode t) {//判断是否为子树 if (t == null) return true; // t 为 null 一定都是 true if (s == null) return false; // 这里 t 一定不为 null, 只要 s 为 null,肯定是 false return isSubtree(s.left, t) || isSubtree(s.right, t) || isSameTree(s,t);//s判是否值相同,s的左右再判断是否是子树 } /** * 判断两棵树是否相同 */ public boolean isSameTree(TreeNode s, TreeNode t){ if (s == null && t == null) return true;//有可能一开始就是两个null是same的,也有可能递归到了最底层它们的值都是相等的 if (s == null || t == null) return false;//注意这里是蟠相同不是判子树了所以不能为null了 if (s.val != t.val) return false;//头结点处的值是否相同 不相等直接false return isSameTree(s.left, t.left) && isSameTree(s.right, t.right);//若相同,判断左子和右子递归该方法来判断值是否相同 } } 作者:kelly2018 链接:https://leetcode-cn.com/problems/subtree-of-another-tree/solution/java-di-gui-ban-by-kelly2018/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
9. 树的对称
101. Symmetric Tree (Easy)
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/
2 2
/ /
3 4 4 3
emmm这每层情况都有变化啊,不能再用上一题和上上题的思路了。
就得从1开始做判断吧?我的思路:把从第二层开始另起方法。。
class Solution { public boolean isSymmetric(TreeNode root) { if(root == null){ return true; } if(root.left.val==root.right.val){ return (yes(root.left,root.rig } return false; } public boolean yes(TreeNode left,TreeNode right){ if(left==null&&right==null){ return true; } if(left == null||right==null){ return false; } if(left.left.val!=right.right.val||left.right.val!=right.left.val){//错了 空指针异常了。。 return false; } return (yes(left.left,left.right)&&yes(right.left,right.right)); } }
答案:

广度周游用队列??没有见过。。
也是从子树第二层开始看。然后我是在主方法中判断他们的两个根结点的值是否相同。相同才可进入下面方法。这样造成了空指针异常且多此一举了。因为其实后面用left.left和right.right再传入后也要判断值是否相等,我没看出这第二层本身就开始递归了。

class Solution { public boolean isSymmetric(TreeNode root) { if(root == null){ return true; } return (yes(root.left,root.right));//改了这里直接传入 } public boolean yes(TreeNode left,TreeNode right){ if(left==null&&right==null){ return true; } if(left == null||right==null){ return false; } if(left.val!=right.val){//改了这里判断传入的两个的值 return false; } return (yes(left.left,right.right)&&yes(left.right,right.left));//改了这里 递归在第二层的子树们开始 } }
方法2:用队列


加入根节点两遍,进入while循环,取出看这俩值相等的话,再加入一个根节点的左子,一个根节点的右子,继续循环。
10. 最小路径
111. Minimum Depth of Binary Tree (Easy)
树的根节点到叶子节点的最小路径长度
这不就是第一题一模一样的思路吗
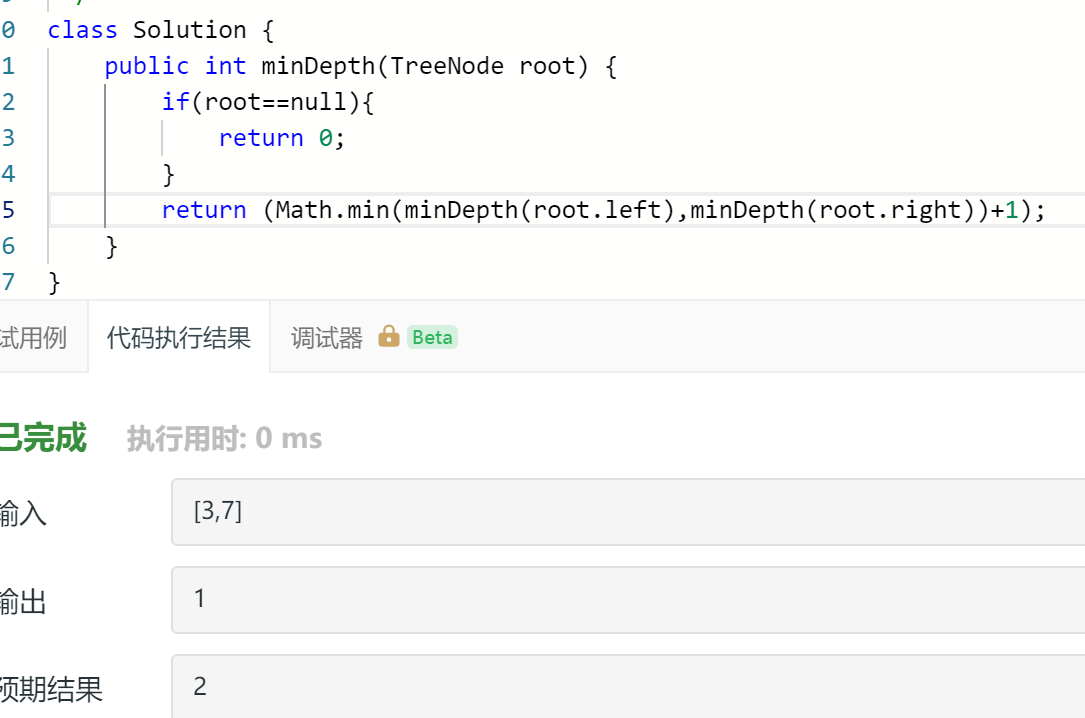
错了。。当只有左子没有右子时,他去选择右子返回0了
不知道咋改。。。
答案:
因为题1是只需要有一条最大就行,不用管子树=null的情况。这里需要考虑一下各种情况。
又改错了。。。

而且这样的顺序错了
答案就得这样顺序:
class Solution { public int minDepth(TreeNode root) { //1.若当前节点为空,直接返回0 if(root==null) return 0; //2.左孩子和有孩子都为空的情况,说明到达了叶子节点,直接返回1即可 if(root.left==null && root.right==null) return 1; //3.如果左孩子和由孩子其中一个为空,说明ldepth1和rdepth有一个必然为0,所以可以返回ldepth + rdepth + 1; int ldepth = minDepth(root.left); int rdepth = minDepth(root.right); if(root.left==null||root.right==null) return ldepth+rdepth+1; //4.最后一种情况,也就是左右孩子都不为空,返回最小深度+1即可 return Math.min(ldepth,rdepth)+1; } }
11. 统计左叶子节点的和
404. Sum of Left Leaves (Easy)
计算给定二叉树的所有左叶子之和。
3
/
9 20
/
15 7
There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
emmm应该要另写方法得出叶子,看答案吧。。
答案这个有点像第二题第三题那样的结构,直接传入root调用方法在方法里判断root(必须从root出发的好像都这样,有一个全局变量用来返回),这里多传入一个false。
class Solution { int sum = 0; public int sumOfLeftLeaves(TreeNode root) { return getSum(root, false); } private int getSum(TreeNode root, boolean isLeft){//传入结点左子值会通过递归全部加到sum里面 if(root != null){ if(isLeft && root.left == null && root.right == null){//满足isLeaf=true,且没有左儿子没有右儿子 sum += root.val;//左叶子和 }else{ getSum(root.left, true);//是左边才设为ture getSum(root.right, false);//如果是求所有叶子节点相加,就把这里为true了 } }
return sum; } } 作者:Omooo 链接:https://leetcode-cn.com/problems/sum-of-left-leaves/solution/chao-ji-rong-yi-li-jie-qi-shi-he-qiu-quan-lu-jing-/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
12. 相同节点值的最大路径长度
687. Longest Univalue Path (Easy)
给定一个二叉树,找到最长的路径,这个路径中的每个节点具有相同值。 这条路径可以经过也可以不经过根节点。
1
/
4 5
/
4 4 5
Output : 2
emmm有点没看懂题目,最长的路径,节点的值有相同的?和哪个相同?
明白了,路径长度为值。就是找最长的路经。
第3题是最大直径,这里是最大路经。
答案和第三题还有点像,但这里要用到值。
跟着第三题的思路只写出求树中以某个结点为根的最大值。。。
class Solution { int total = 0; public int longestUnivaluePath(TreeNode root) { maxLength(root); return total; } public int maxLength (TreeNode root){ if(root==null){ return 0; } int L,R; L=maxLength(root.left); R=maxLength(root.right); total = Math.max(L+R+root.val,total); return (Math.max(L,R))+root.val; } }
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { private int path = 0; public int longestUnivaluePath(TreeNode root) { dfs(root); return path; } private int dfs(TreeNode root){//DFS深度优先搜索 返回值为路径 if (root == null) return 0; int left = dfs(root.left); int right = dfs(root.right); int leftPath = root.left != null && root.left.val == root.val ? left + 1 : 0;//?? int rightPath = root.right != null && root.right.val == root.val ? right + 1 : 0;//??? path = Math.max(path, leftPath + rightPath); return Math.max(leftPath, rightPath); } }
可能还是没理解题目。。。看不懂代码。。。
先跳了。。。
明白了 他是找一条值全部相同的最长路径,不一定经过当前的根节点
class Solution { int ans; public int longestUnivaluePath(TreeNode root) { ans = 0; longestPath(root); return ans; } //递归函数功能:搜寻以node为起点的最长同值路径:要么是以node为起点的左子树,要么是以node为起点的右子树 public int longestPath(TreeNode node) { if (node == null) return 0; int maxLorRres=0; int left = longestPath(node.left); //node左子树的最长同值路径 int right = longestPath(node.right);//node右子树的最长同值路径 //这种情况对于寻找最长同值路径长有帮助,对于搜索以root为路径起始点的最长路径没有帮助 if (node.left != null && node.left.val == node.val&&node.right != null && node.right.val == node.val) { ans=Math.max(ans, left + right+2); } //从左右子树中选择最长的同值路径 if(node.left!=null&&node.left.val == node.val){ maxLorRres=left+1; } if(node.right!=null&&node.right.val==node.val){ maxLorRres=Math.max(maxLorRres,right+1); } //从ans与maxLorRres中更新最大值 ans=Math.max(ans,maxLorRres); return maxLorRres; //所以你能知道为什么返回这个值了吗?
回答一下为什么最后返回的maxLorRres而不是ans,首先这个递归函数的返回值是Int,肯定用来计数的。
ans其实是作者利用这个递归函数在函数中所求的值,与递归条件,返回值什么无关,那么所有的递归出口都将在int maxLorRres=0;这行代码之后,
则 maxLorRres则是已经被申明了,后续的if判断条件则是在统计这个 maxLorRres的值,而递归的形式则是递归左子树或者右子树 } } 作者:Chuancey 链接:https://leetcode-cn.com/problems/longest-univalue-path/solution/guan-yu-di-gui-si-lu-de-chao-xiang-xi-ge-ren-jian-/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
13. 间隔遍历
337. House Robber III (Medium)
3
/
2 3
3 1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
直接看答案:
总体思路为:分别计算单层数据的和与双层数据的和,返回较大的那个值。其实就是简单递归的应用啊。。没反应过来递归结构。。
单层数据之和的计算:当前节点的值,加上左子节点的两个子节点的和,再加上右子节点的两个子节点的和。
双层数据之和的计算:当前节点的两个子节点的值之和。
class Solution { public int rob(TreeNode root) { //若当前节点为null,直接返回0 if(root==null) return 0; //计算val1(表示单层数据的和) int val1=root.val;//重要!!!! //如果当前节点的左节点不为null,那就将当前节点的值加上左节点的两个子节点的值 if(root.left!=null) val1+=rob(root.left.left)+rob(root.left.right); //如果当前节点的右节点不为null,那就将当前节点的值加上右节点的两个子节点的值 if(root.right!=null) val1+=rob(root.right.left)+rob(root.right.right); //计算val2(表示双层数据的和)只用看它的左右节点 int val2=rob(root.left)+rob(root.right); //返回val1与val2中更大的那个值 return Math.max(val1,val2); } }
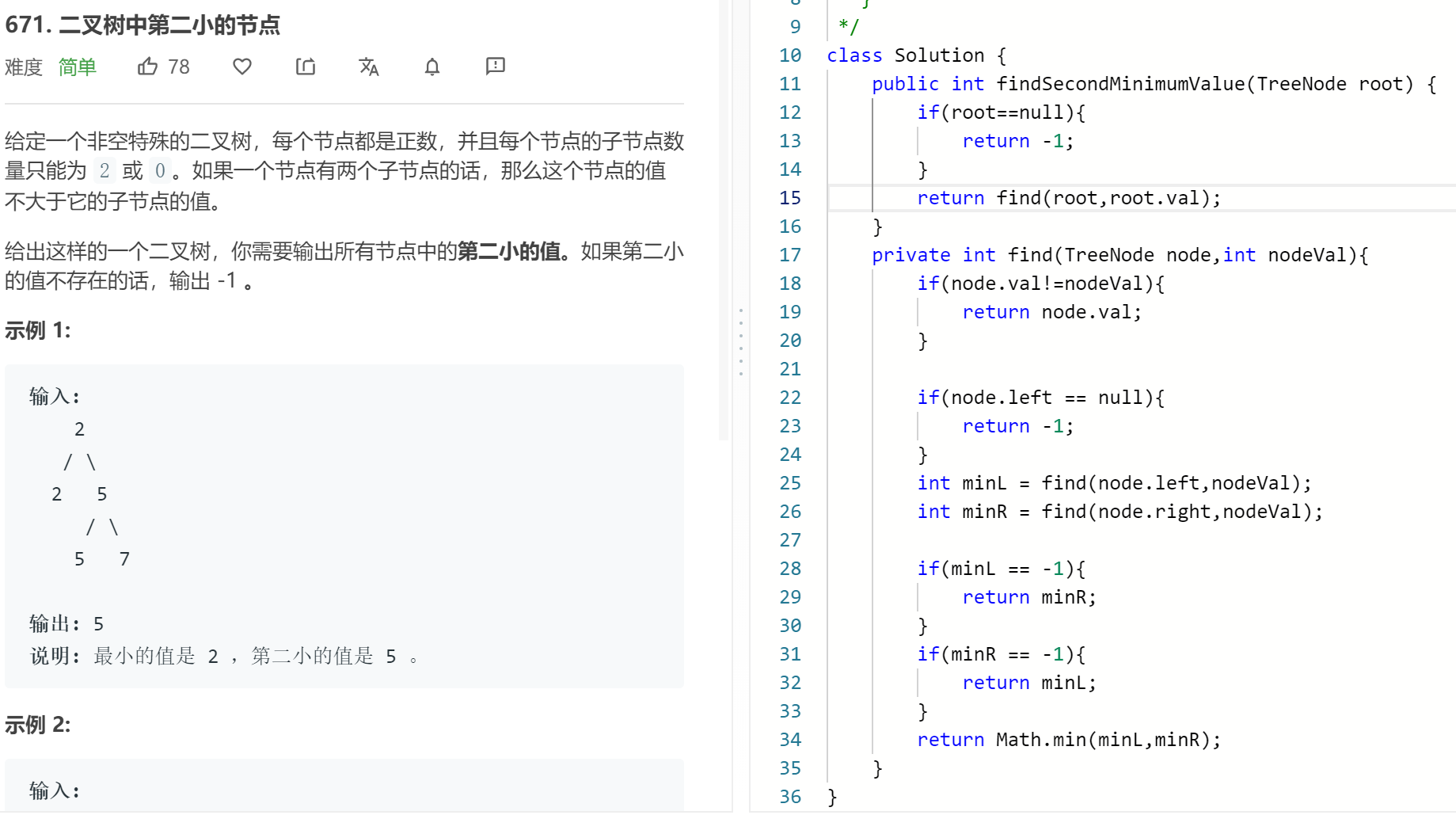
14. 找出二叉树中第二小的节点
671. Second Minimum Node In a Binary Tree (Easy)
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么这个节点的值不大于它的子节点的值。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。
Input:
2
/
2 5
/
5 7
Output: 5
一个节点要么具有 0 个或 2 个子节点,如果有子节点,那么根节点是最小的节点。
我的思路用起了优先队列。。但是不知道怎么遍历取到有左右子的结点。。。
答案:
原来人家本来就是排好序的。。从小到大。。。
思路分析:
首先根据题目描述,根结点值一定小于或者等于子结点值,这就是一个最小堆,根结点值就是整个树中的最小值,所以要找的第二小值,就是除去根结点值的最小值,为了方便使用rootValue表示这棵树根节点的值。
树的题一般考虑递归。考虑到题目所求,递归函数的返回值应该定义为以节点x为根的树中非rootValue的最小值。由于一直需要信息rootValue,所以递归函数的参数除了结点还有rootValue。(这就有点想isLeft的那个题了)
对于以TreeNode x为根的结点,
如果其值不为rootValue,那么它的值就是以它为根的树中非根结点值的最小值。
如果它的值为rootValue,而且其已经是叶子结点x.left == null,在以它为根的树中没有找到非根结点值的最小值,返回失败标志-1。
如果它的值为rootValue,但它还有左右子树,就去找左右子树的非根结点值的最小值,分别为leftMin, rightMin。
如果leftMin == -1,左子树查找失败,返回右子树的查找结果(也可能是失败,但失败也是返回-1,也还是rightMin)。
同理rightMin == -1,返回左子树的查找结果
如果左右都没有查找失败,都找到了非根结点值的局部最小值,就要选择其中更小的一个返回。
时间复杂度为O(n)O(n), 空间复杂度与树高成正比。
class Solution { public int findSecondMinimumValue(TreeNode root) { if(root == null) return -1; return find(root, root.val); } /** * 按照题目描述,这个最上面的元素就是最小的元素。用rootValue表示最小值 * 找到和rootValue值不相同的最小值,与rootValue不相同的最小值其实就是第二小的值。 */ private int find(TreeNode x, int rootValue){ if(x.val != rootValue) // 如果当前结点不等于根结点,那么值为以x为根的最小的非rootValue的值。 return x.val;//递归终点1
// 这之下都是 当前结点值为根结点值的情况 if(x.left == null) // 如果它的值为rootValue,而且其已经是叶子结点x.left == null,在以它为根的树中没有找到非根结点值的最小值,返回失败标志-1。 return -1;//递归终点2
int leftMin = find(x.left, rootValue);//左右两边分别找最小值,因为递归终点1或2出来的一定是不等于root值的第2小的val或者-1 int rightMin = find(x.right, rootValue);//传入的还是最小值,根结点的值!
if(leftMin == -1) return rightMin; if(rightMin == -1) return leftMin;
return Math.min(leftMin, rightMin);//左右两边比较各自的最小值 } } }
作者:ustcyyw
链接:https://leetcode-cn.com/problems/second-minimum-node-in-a-binary-tree/solution/671java-0msdi-gui-hen-jian-ji-e-by-ustcyyw/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
哎呀好难啊不会
从230来的,想到了671所以理解了理解了。。