LeetCode哈希表专题

哈希表使用 O(N) 空间复杂度存储数据，并且以 O(1) 时间复杂度求解问题。

1.Java 中的 HashSet 用于存储一个集合，可以查找元素是否在集合中。如果元素有穷，并且范围不大，那么可以用一个布尔数组来存储一个元素是否存在（？？有点不理解，还没碰到过这样的题。。。）例如对于只有小写字符的元素，就可以用一个长度为 26 的布尔数组来存储一个字符集合，使得空间复杂度降低为 O(1)。

2.Java 中的 HashMap 主要用于映射关系，从而把两个元素联系起来。HashMap 也可以用来对元素进行计数统计，此时键为元素，值为计数。和 HashSet 类似，如果元素有穷并且范围不大，可以用整型数组来进行统计。在对一个内容进行压缩或者其它转换时，利用 HashMap 可以把原始内容和转换后的内容联系起来。例如在一个简化 url 的系统中 【Leetcdoe : 535. Encode and Decode TinyURL (Medium)】

一.HashMap

是Map接口最常用的实现类，采用哈希算法来实现，存放键值对（Map的特性）

特点是键（key）不重复，线程不安全，效率高，允许key或value为null。

结构为：数组+链表

常用方法总结：

1.加入键值对：对象名称.put(key，value)，若键重复，新的值对会覆盖旧的值。

2.HashMap的容量（长度）：对象名称.size( )

3.返回布尔类型，验证当前HashMap中是否存在指定的key：对象名称.containsKey(key）

4.返回布尔类型，验证当前HashMap中是否存在指定的value：对象名称.containsValue(value)

5.返回一个包含所有的key的Set：对象名称.keySet( )

6.返回一个包含所有的Value的Collection：对象名称.values( )

7.返回布尔类型，验证当前HashMap是否为空：对象名称.isEmpty( )

8.清空当前HashMap：对象名称.clear( )

9.返回指定key对应的value，如果该key不存在，返回null：对象名称.get(key)

10.返回指定key对应的value，如果该key不存在，返回指定的默认内容：对象名称.getOrDefault(key,defaultValue)

11.将指定HashMap中的所有键值对复制到当前HashMap中：对象名称.putAll(指定HashMap对象名称)

二.HashSet

HashSet是Set接口最常用的一个实现类。

Set接口继承自Collection，Set接口中没有新增方法，方法和Collection保持完全一致。因此Set的方法与List完全相同。

Set容器特点：无序、不可重复。无序指Set中的元素没有索引，我们只能遍历查找。

不可重复指不允许加入重复的元素。更确切地讲，新元素如果和Set中某个元素通过equals()方法对比为true，则不能加入。甚至，Set中也只能放入一个null元素，不能多个。

HashSet底层实现（本质上是HashMap）

常用方法：add ()，clear()，contains()，isEmpty，remove()，size()

1. Two Sum (Easy)

给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。

Leetcode / 力扣

哎呀我去。。。不写一下真不知道自己双指针都能写错。。。这不是有序数组啊！！老老实实用嵌套吧。。。不要用while(i<j)

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int length = nums.length;
        for(int i = 0;i<length;i++){
            int current = nums[i];
            for(int j = length-1;j>i;j--){
                if(current+nums[j]==target){
                    return new int[] {i,j};
                }
            }
        }
        return null;
    }
}

方法二：哈希表

是把元素值当键！！！索引当值!（等一下，元素值当key没有重复？？可能题目规定了。。）

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int length = nums.length;
        Map<Integer,Integer> map = new HashMap<>();
        for(int i = 0;i<length;i++){
            if(map.containsKey(target-nums[i])){//用key找另一个元素值
                return new int[] {map.get(target-nums[i]),i};//通过key为另一个元素的值，来拿到map中对应存的索引
            }else{
                map.put(nums[i],i);//元素值为key,索引为值
            }
        }
        return null;
    }
}

2. 判断数组是否含有重复元素

217. Contains Duplicate (Easy)

给定一个整数数组，判断是否存在重复元素。

如果任意一值在数组中出现至少两次，函数返回 true 。如果数组中每个元素都不相同，则返回 false 。

Leetcode / 力扣

我是用长度来判断的，因为nums中有重复值当做key时会自动覆盖原来的value。答案也是，但是更简洁。。。用forecah不考虑i时直接用Set!!!

class Solution {
    public boolean containsDuplicate(int[] nums) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i =0;i<nums.length;i++){
            map.put(nums[i],i);
        }
        if(map.size()==nums.length){
            return false;
        }
        return true;
    }
}

答案：（这就是HashSet的用法，前面不理解的现在理解了。我想到了不用用索引准备改成list，但是list并不会自动覆盖。原来是得用set啊啊啊啊）

public boolean containsDuplicate(int[] nums) {
    Set<Integer> set = new HashSet<>();
    for (int num : nums) {
        set.add(num);
    }
    return set.size() < nums.length;
}

3. 最长和谐序列

594. Longest Harmonious Subsequence (Easy)

和谐数组是指一个数组里元素的最大值和最小值之间的差别正好是1。

现在，给定一个整数数组，你需要在所有可能的子序列中找到最长的和谐子序列的长度。

Leetcode / 力扣

emmm???不会做

答案：

我们可以用一个哈希映射（HashMap）来存储每个数出现的次数，这样就能在 O(1)O(1) 的时间内得到 x 和 x + 1 出现的次数。

我们首先遍历一遍数组，得到哈希映射。随后遍历哈希映射，设当前遍历到的键值对为 (x, value)，那么我们就查询 x + 1 在哈希映射中对应的值，就得到了 x 和 x + 1 出现的次数。

明白了，还是map计数来做。

class Solution {
    public int findLHS(int[] nums) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int x:nums){
            map.put(x,map.getOrDefault(x,0)+1);
        }
        //然后遍历map
        int max = 0;
        for(int x:map.keySet()){
            if(map.containsKey(x+1)){//这个边界条件别忽略，不然一直空指针异常
            max=Math.max(map.get(x)+map.get(x+1),max);
            }
        }
        return max;
    }
}

4. 最长连续序列

128. Longest Consecutive Sequence (Hard)

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

Leetcode / 力扣

emmm排个序都不止O(n)了吧？？不会做。。

答案：

方法一：哈希表
思路和算法

我们考虑枚举数组中的每个数 x，考虑以其为起点，不断尝试匹配 x+1,x+2,⋯ 是否存在，假设最长匹配到了x+y，那么以 x 为起点的最长连续序列即为 x,x+1,x+2,⋯,x+y，其长度为 y+1，我们不断枚举并更新答案即可。

对于匹配的过程，暴力的方法是 O(n) 遍历数组去看是否存在这个数，但其实更高效的方法是用一个哈希表存储数组中的数，这样查看一个数是否存在即能优化至 O(1) 的时间复杂度(map中查看一个数很快)。仅仅是这样我们的算法时间复杂度最坏情况下还是会达到 O(n^2)（即外层需要枚举 O(n) 个数，内层需要暴力匹配 O(n) 次），无法满足题目的要求。但仔细分析这个过程，我们会发现其中执行了很多不必要的枚举，如果已知有一个 x, x+1,x+2,⋯,x+y 的连续序列，而我们却重新从 x+1，x+2或者是 x+y 处开始尝试匹配，那么得到的结果肯定不会优于枚举 x 为起点的答案，因此我们在外层循环的时候碰到这种情况跳过即可。

那么怎么判断是否跳过呢？由于我们要枚举的数 x 一定是在数组中不存在前驱数 x−1 的，不然按照上面的分析我们会从 x−1 开始尝试匹配，因此我们每次在哈希表中检查是否存在 x−1 即能判断是否需要跳过了。

增加了判断跳过的逻辑之后，时间复杂度是多少呢？外层循环需要 O(n) 的时间复杂度，只有当一个数是连续序列的第一个数的情况下才会进入内层循环，然后在内层循环中匹配连续序列中的数，因此数组中的每个数只会进入内层循环一次。根据上述分析可知，总时间复杂度为 O(n)，符合题目要求。

跳过的过程：

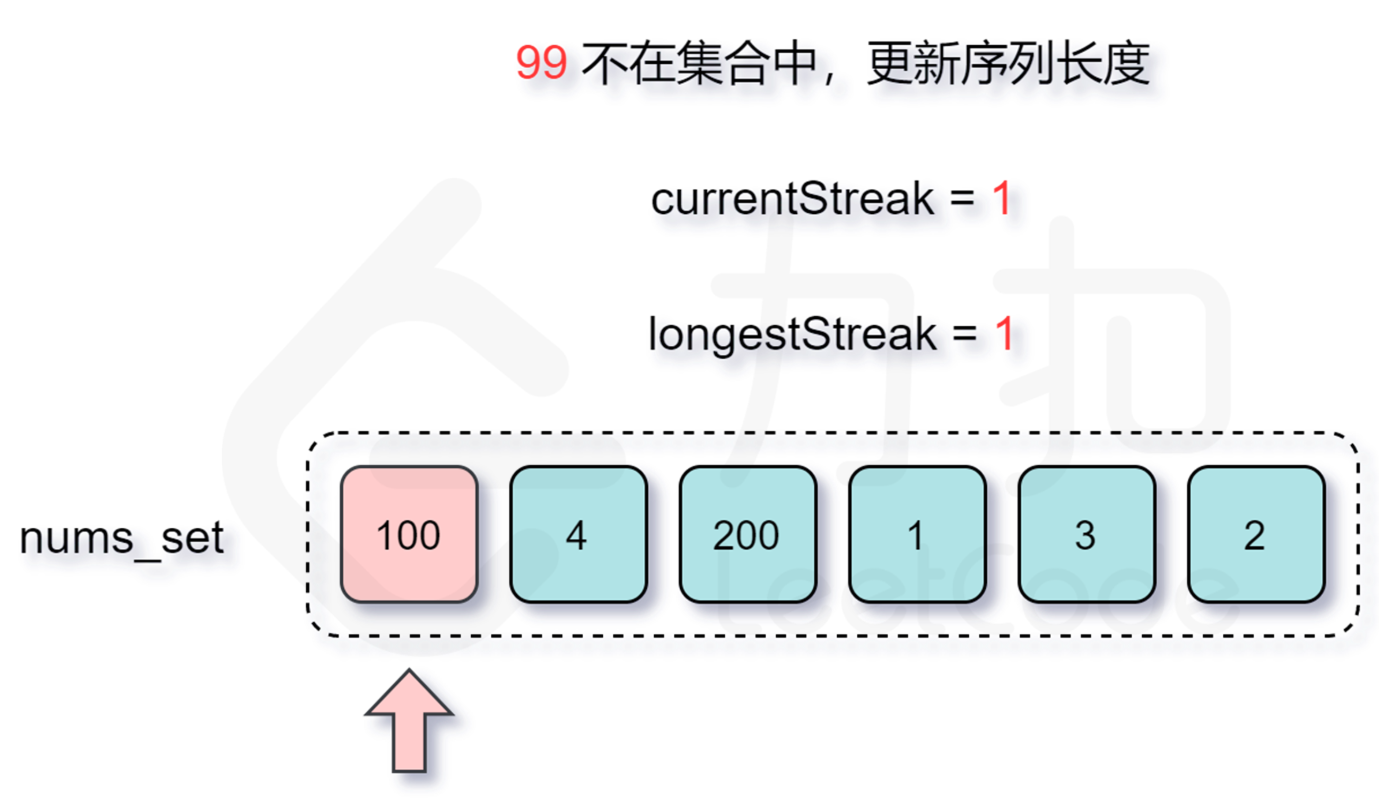
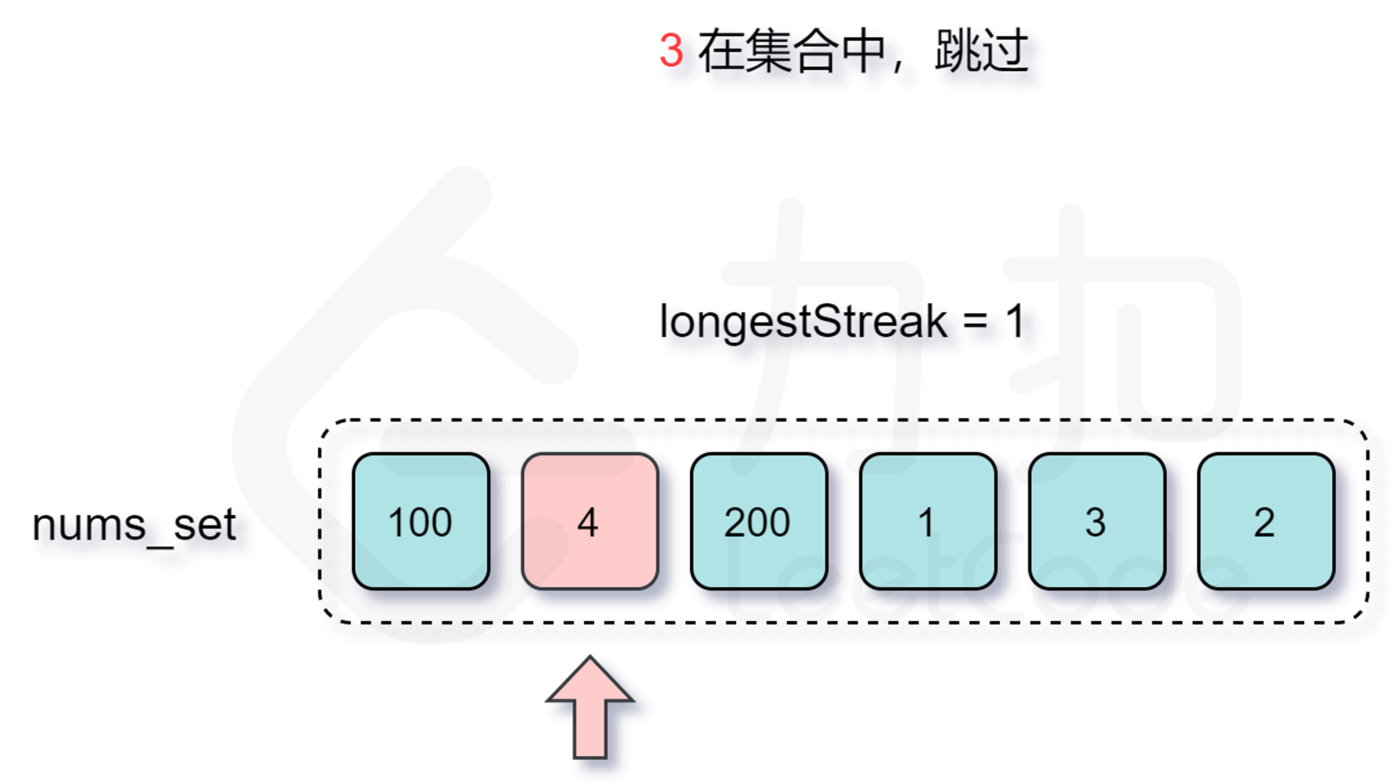
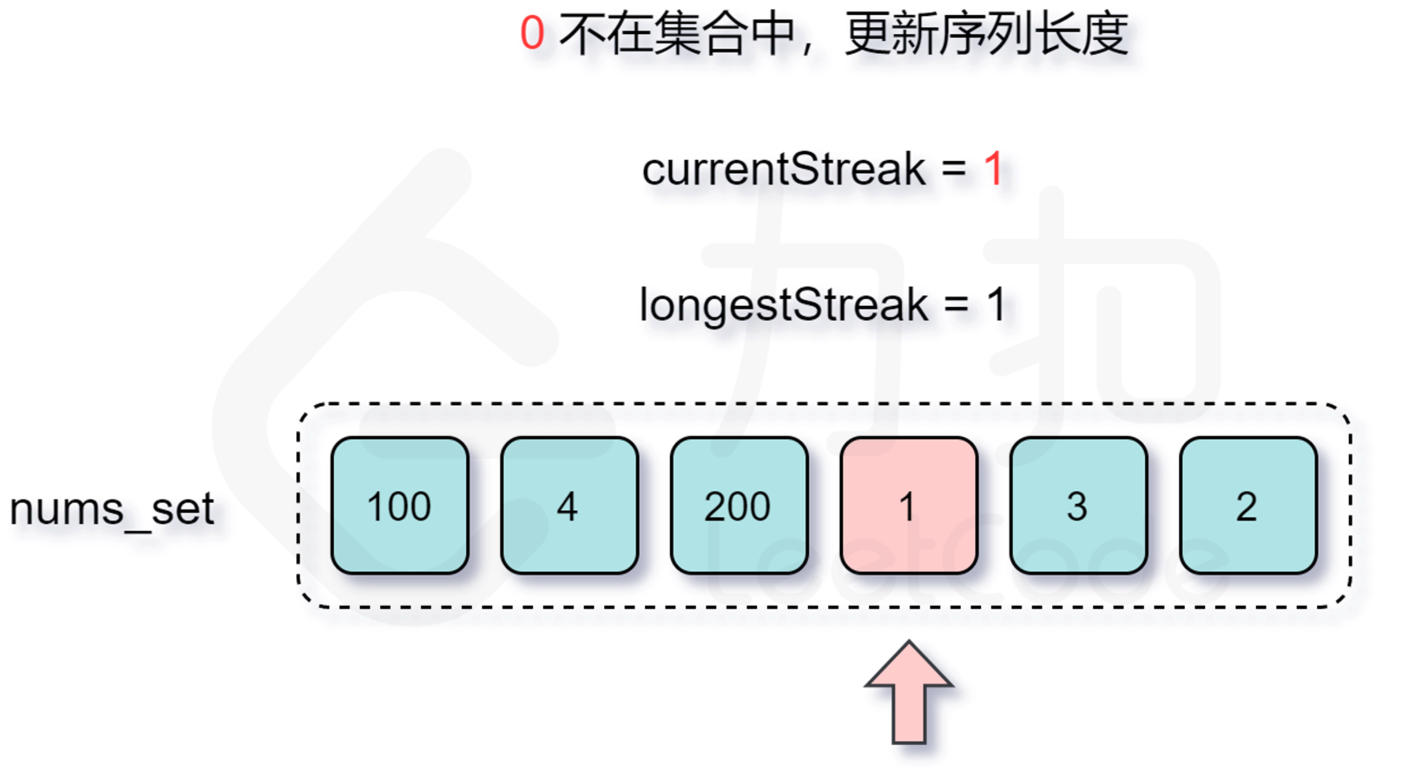
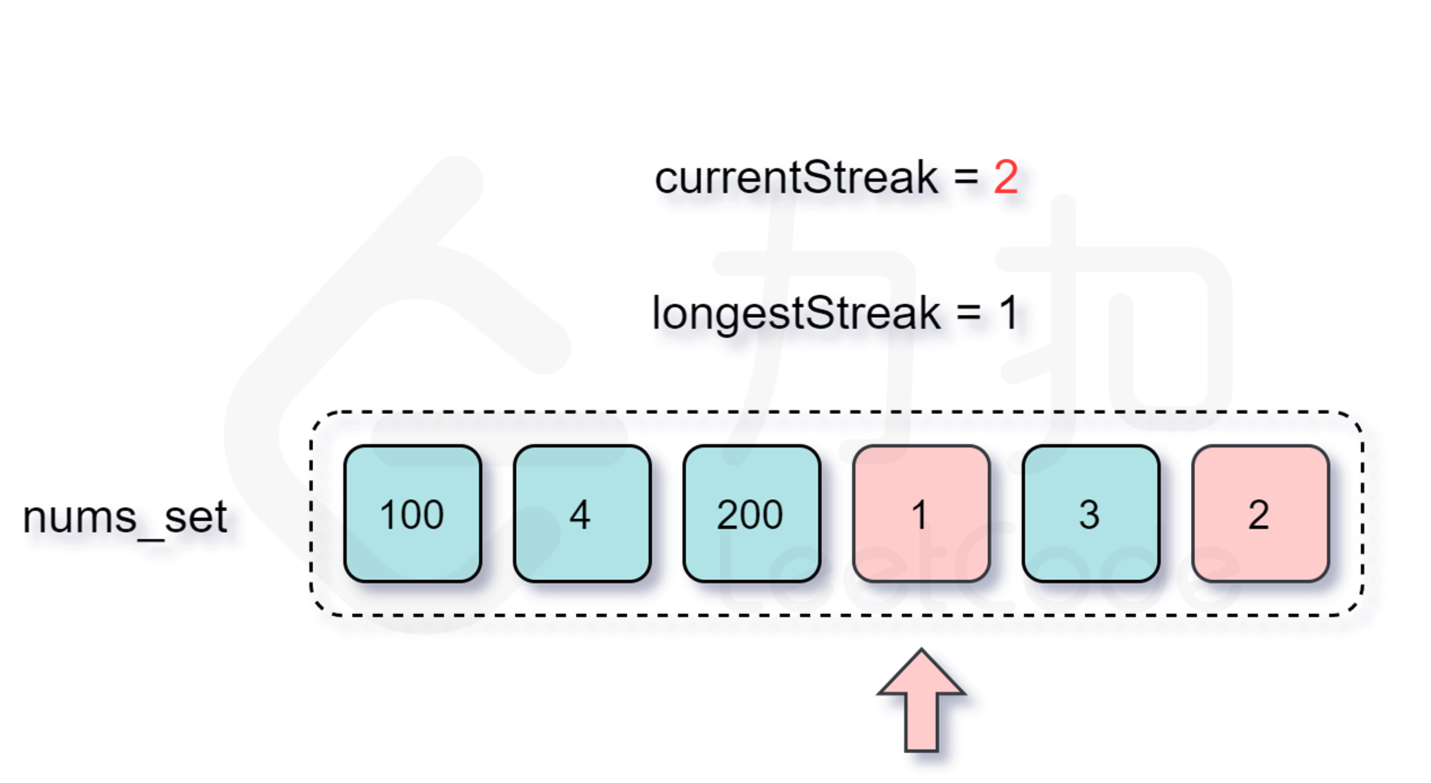
然后2,3,4都在。。

代码：

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> num_set = new HashSet<Integer>();//如何new一个Set
        for (int num : nums) {
            num_set.add(num);//add不是put了。。。list一样
        }//用set装nums，去重。 这里不是时间复杂度，是空间复杂度（？why？？

        int longestStreak = 0;

        for (int num : num_set) {//遍历set O（n）时间复杂的
            if (!num_set.contains(num - 1)) {//跳过的是包含的 不包含的才是可以被视为连续序列的开头的 注意是contains不是containsKey...
                int currentNum = num;
                int currentStreak = 1;

                while (num_set.contains(currentNum + 1)) {//比如1碰到有2有3有4 while循环判断！！！
                    currentNum += 1;//连续的值们
                    currentStreak += 1;
                }

                longestStreak = Math.max(longestStreak, currentStreak);
            }
        }

        return longestStreak;
    }
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/longest-consecutive-sequence/solution/zui-chang-lian-xu-xu-lie-by-leetcode-solution/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。