二叉搜索树03--[重构二叉树&&前驱节点&&后驱节点&&代码重构&&删除节点]

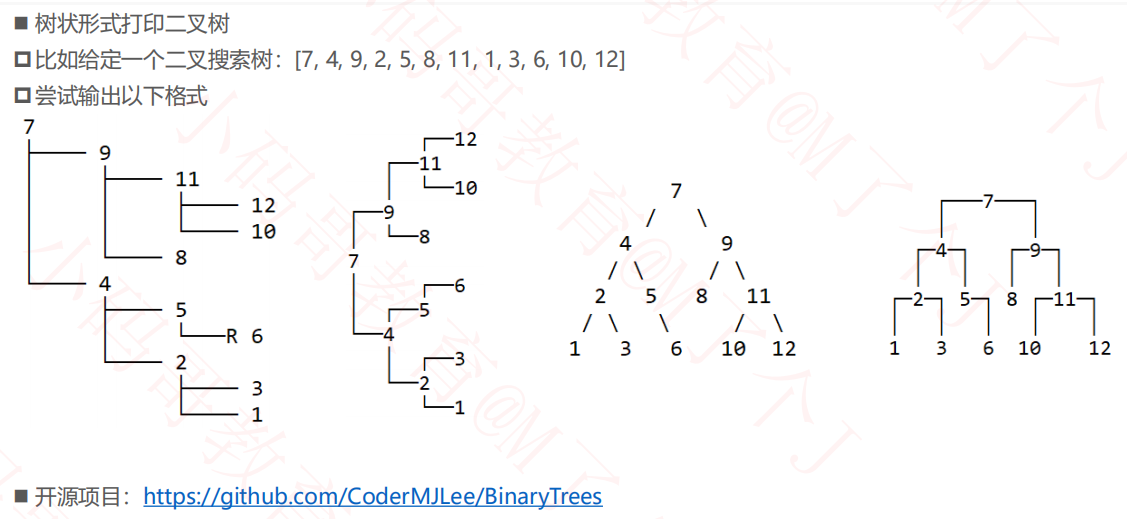
1.重构二叉树

 1.1前序遍历+中序遍历重构二叉树

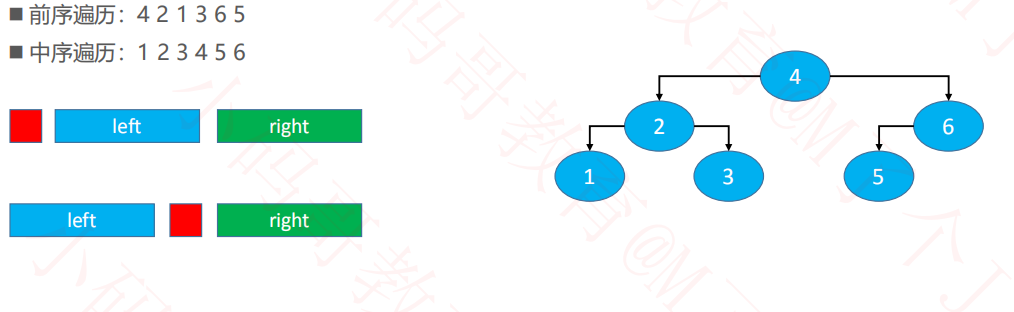
 1.2前驱节点

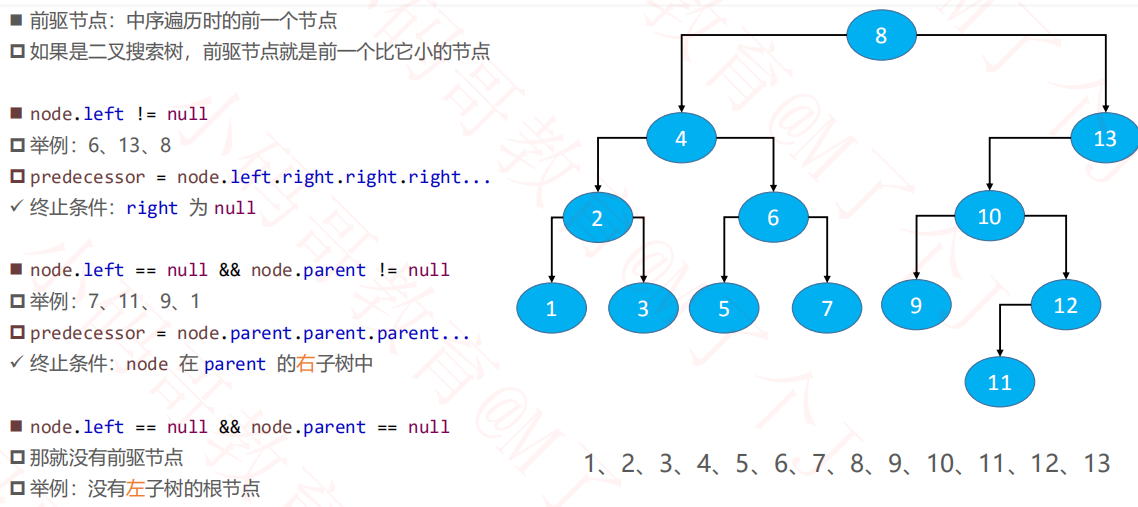
 1.3后继节点

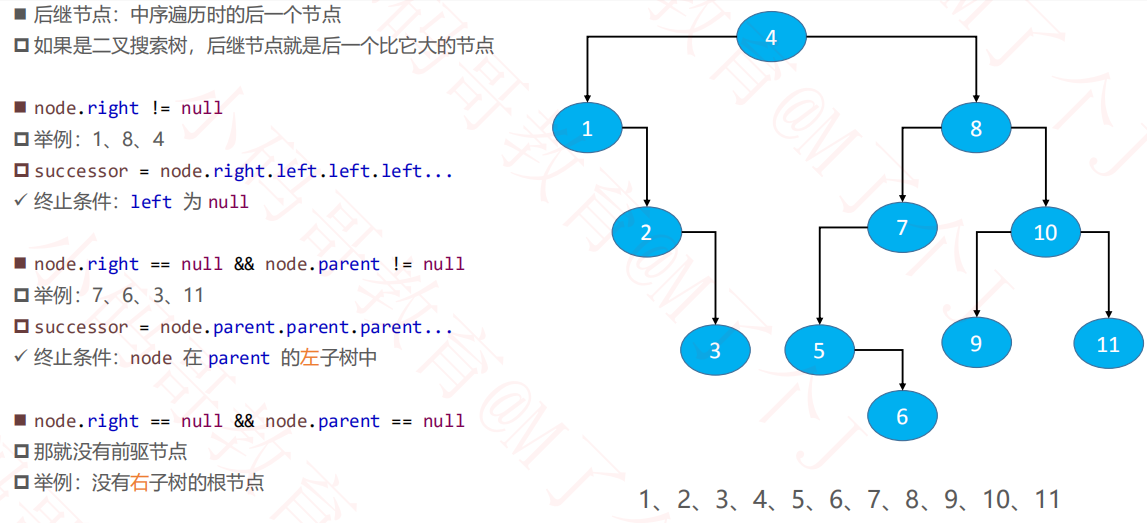
1.4根据元素获取节点

 

2.删除节点

2.1删除叶子节点

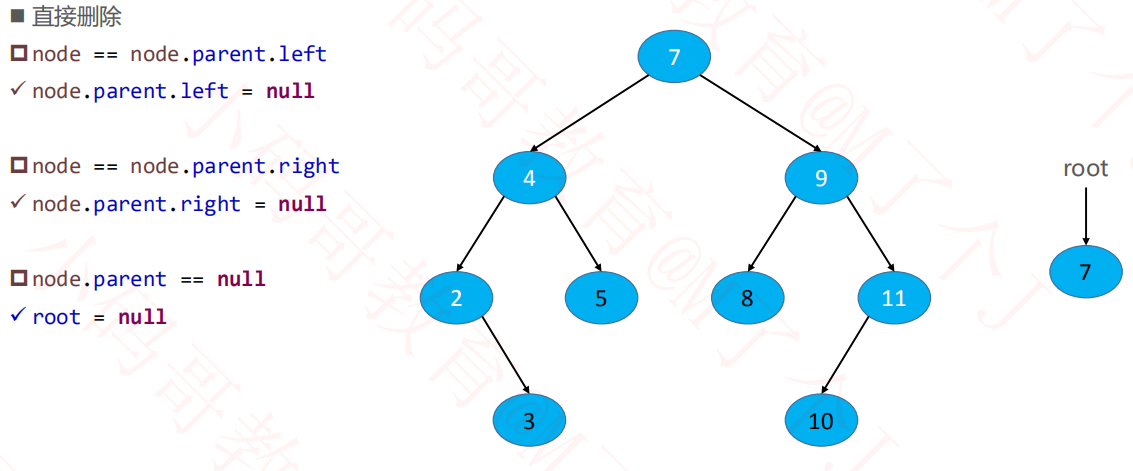
 2.2删除度为1的节点

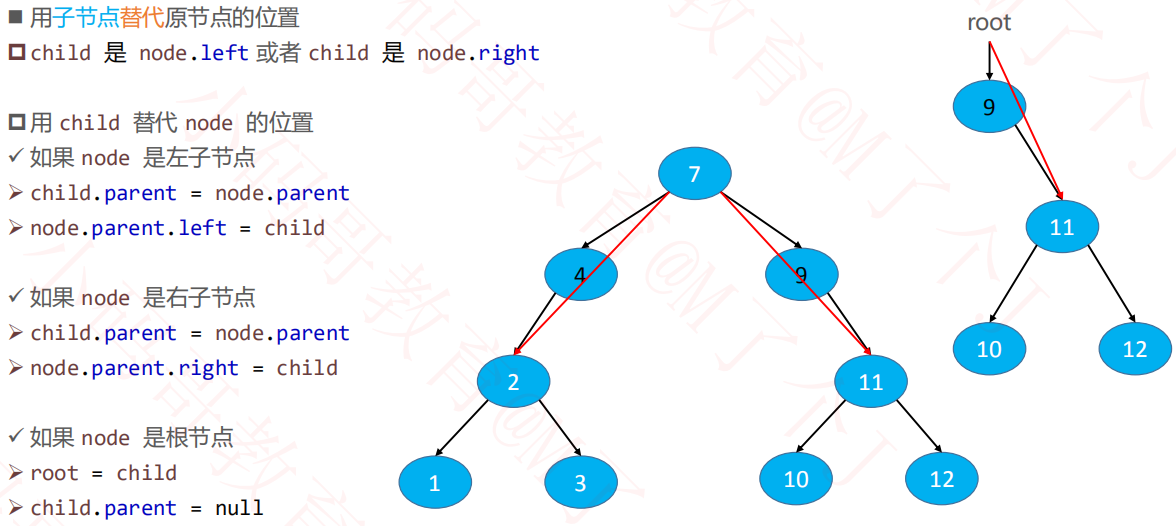
 2.3删除度为3的节点

 2.4相关代码

public void remove(E element) {
        remove(node(element));
    }

    public boolean contains(E element) {
        return node(element) != null;
    }
    
    private void remove(Node<E> node) {
        if (node == null) return;
        
        size--;
        
        if (node.hasTwoChildren()) { // 度为2的节点
            // 找到后继节点
            Node<E> s = successor(node);
            // 用后继节点的值覆盖度为2的节点的值
            node.element = s.element;
            // 删除后继节点
            node = s;
        }
        
        // 删除node节点（node的度必然是1或者0）
        Node<E> replacement = node.left != null ? node.left : node.right;
        
        if (replacement != null) { // node是度为1的节点
            // 更改parent
            replacement.parent = node.parent;
            // 更改parent的left、right的指向
            if (node.parent == null) { // node是度为1的节点并且是根节点
                root = replacement;
            } else if (node == node.parent.left) {
                node.parent.left = replacement;
            } else { // node == node.parent.right
                node.parent.right = replacement;
            }
        } else if (node.parent == null) { // node是叶子节点并且是根节点
            root = null;
        } else { // node是叶子节点，但不是根节点
            if (node == node.parent.left) {
                node.parent.left = null;
            } else { // node == node.parent.right
                node.parent.right = null;
            }
        }
    }
    
    private Node<E> node(E element) {
        Node<E> node = root;
        while (node != null) {
            int cmp = compare(element, node.element);
            if (cmp == 0) return node;
            if (cmp > 0) {
                node = node.right;
            } else { // cmp < 0
                node = node.left;
            }
        }
        return null;
    }
    public boolean hasTwoChildren() {
            return left != null && right != null;
        }
    private Node<E> successor(Node<E> node) {
        if (node == null) return null;
        
        // 前驱节点在左子树当中（right.left.left.left....）
        Node<E> p = node.right;
        if (p != null) {
            while (p.left != null) {
                p = p.left;
            }
            return p;
        }
        
        // 从父节点、祖父节点中寻找前驱节点
        while (node.parent != null && node == node.parent.right) {
            node = node.parent;
        }

        return node.parent;
    }

3.重构代码

4.练习