这是一个神奇的课题,其实我觉得用一个词来形容这个算法挺合适的:暴力。
是啊,就是循环+暴力。没什么难的。。。
先来看一道裸题。

那么对于这道题,显然我们的暴力算法就是枚举区间的左右端点,然后通过前缀和统计结果。时间复杂度O(n^2),但是如果我们的数据范围到了100000,那么我们的算法就T了。
于是我们考虑一个性质。如果我们发现一个区间,这个区间的sum<k,那么被这个区间包含的区间都不可能是答案。
所以我们用两个指针(左右端点。)如果目前区间的sum<k,我们就延伸右端点。否则我们就统计答案,然后让左端点往右移。直到2个指针都到达n,结束枚举。
这显然很水对吧。
那么我们来一道稍难的问题。

那么我们先想一下我们的策略,假如我们把所有的区间按照区间长度排序,那么我们的答案一定是其中的连续一段区间。因为跳着取肯定没有连着取更优。
那么我们接下来就是判断区间的覆盖次数了。显然我们可以用线段树轻松解决这个问题。
说起来挺简单,其实实现起来还是挺复杂的。
下面贴上代码
#include<cstdio> #include<algorithm> #define min(a,b) ((a)<(b)?(a):(b)) #define max(a,b) ((a)>(b)?(a):(b)) #define ls (k<<1) #define rs (k<<1|1) #define M 500005 #define MN 1<<20 #define inf 0x3f3f3f3f using namespace std; int n,m,cnt,l[M],r[M],rk[M],val[M<<1],t[MN<<1],ans=inf,mark[MN<<1],len[M]; int find(int x){ int le=1,re=cnt; while(le<re){ int mid=le+re>>1; if(val[mid]<x)le=mid+1; else re=mid; }return le; } void pushdown(int k){mark[ls]+=mark[k],mark[rs]+=mark[k],t[ls]+=mark[k],t[rs]+=mark[k],mark[k]=0;} void fpush(int k){t[k]=max(t[ls],t[rs]);} void update(int l,int r,int a,int b,int k,int ad){ if(a<=l&&r<=b){mark[k]+=ad;t[k]+=ad;return;}if(l!=r&&mark[k])pushdown(k);int mid=l+r>>1; if(a<=mid)update(l,mid,a,b,ls,ad); if(b>mid)update(mid+1,r,a,b,rs,ad); fpush(k); } bool cmp(int a,int b){return len[a]>len[b];} int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)scanf("%d%d",&l[i],&r[i]),len[i]=r[i]-l[i],rk[i]=i,val[i<<1]=l[i],val[i<<1|1]=r[i]; sort(val+2,val+(n<<1)+2);sort(rk+1,rk+n+1,cmp); for(int i=3;i<=(n<<1)+1;i++)if(val[i-1]!=val[i])val[++cnt]=val[i]; for(int i=1;i<=n;i++)l[i]=find(l[i]),r[i]=find(r[i]); for(int le=1,re=1;le<=n;le++) for(update(1,cnt,l[rk[le]],r[rk[le]],1,1);t[1]>=m;re++){ update(1,cnt,l[rk[re]],r[rk[re]],1,-1); ans=min(len[rk[re]]-len[rk[le]],ans); } printf("%d ",ans==inf?-1:ans); }
————————————————我是分割线————————————————
第一块讲完啦!接下来第二块。
矩阵快速幂=矩阵+快速幂。。
我记得我讲过。。但是博客不见了⌇●﹏●⌇吓死宝宝惹
无奈的重讲一遍。
首先我们要了解一下矩阵。。(虽然我们夏令营的时候讲过,但是显然向量内积什么的特别难理解,所以我们不要管理念)
总之就是n*m个数的集合。
然后我们理解一下矩阵乘法的定义
直接上图

那么我们用矩阵乘法解决什么问题呢?
答:dp问题。
是不是很奇怪?
但是其实并不难理解、
我们举个例子。
假设我们已知DP式子:dp[i]=dp[i-1]+dp[i-2],假如我们想要直接得到dp的第n项,而且n的值特别大,比如10^18,那么显然我们不能On推过去。
那怎么办呢?我们可以把dp方程转移为一个矩阵。
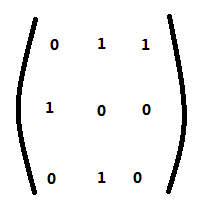
那么我们得到的这个矩阵表示,假如说我们把矩阵的第一位变为矩阵的第二位和矩阵的第三位之和,把矩阵的第二位变为矩阵的第一位,矩阵的第三位变为矩阵的第二位。
由于每次的转移方程都不变,所以我们只要把这个矩阵做快速幂就好了。
是不是很简单?
下面贴上例题&&代码
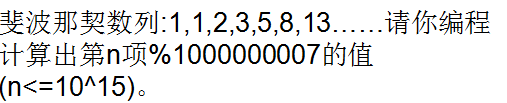
代码:
#include<cstdio> #include<cstring> using namespace std; #define ll long long #define MOD 1000000007 struct mat { int z[2][2]; mat(){memset(z,0,sizeof(z));} mat operator*(mat b) { mat c;int i,j,k; for(i=0;i<2;++i)for(j=0;j<2;++j) for(k=0;k<2;++k)c.z[i][j]=(c.z[i][j]+(ll)z[i][k]*b.z[k][j])%MOD; return c; } }f,x; mat pow(ll x) { mat r=f,t=f; for(--x;x;x>>=1,t=t*t)if(x&1)r=r*t; return r; } int main() { ll n; f.z[0][1]=f.z[1][0]=f.z[1][1]=1; x.z[0][0]=x.z[0][1]=1; scanf("%lld",&n); printf("%d",(x*pow(n-1)).z[0][0]); }