2019/3/31acm周三(三人)/LightOJ

LightOJ - 1005 坑爆(注意空格会提醒wa)

LightOJ - 1005

A rook is a piece used in the game of chess which is played on a board of square grids. A rook can only move vertically or horizontally from its current position and two rooks attack each other if one is on the path of the other. In the following figure, the dark squares represent the reachable locations for rook R1 from its current position. The figure also shows that the rook R1 and R2 are in attacking positions where R1 and R3 are not. R2 and R3 are also in non-attacking positions.

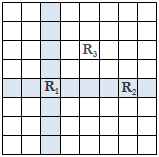
Now, given two numbers n and k, your job is to determine the number of ways one can put k rooks on an n x n chessboard so that no two of them are in attacking positions.

Input
Input starts with an integer T (≤ 350), denoting the number of test cases.

Each case contains two integers n (1 ≤ n ≤ 30) and k (0 ≤ k ≤ n2).

Output
For each case, print the case number and total number of ways one can put the given number of rooks on a chessboard of the given size so that no two of them are in attacking positions. You may safely assume that this number will be less than 1017.

Sample Input
8
1 1
2 1
3 1
4 1
4 2
4 3
4 4
4 5

Sample Output
Case 1: 1
Case 2: 4
Case 3: 9
Case 4: 16
Case 5: 72
Case 6: 96
Case 7: 24
Case 8: 0

题意：n*n的棋盘，放入k个车，要使k个车不相互攻击，有多少种方案。
思路：对角分布，组合，先排列，再除去重复的互换位置。
A（n，k）*A（n，k）/ A（k，k）；
即得C（n， k）*A（n， k）
以下为空格的wa，很难受！！！

#include <map>
#include <iostream>
#include <algorithm>
#include <string>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <math.h>
#include <climits>
#include <queue>
#include <iomanip>！
#include <vector>
#define ll long long
#include <stdio.h>
using namespace std;

int main()
{
    //ios::sync_with_stdio(false);
    ll n;
    scanf("%lld",&n);
    for(ll j=1;j<=n;j++)
    {
        ll a,b;
        scanf("%lld%lld",&a,&b);
        printf("Case %d: ",j);//注意题目中这里有 空格 坑爆！！！
        ll sum=1;
        for(ll i=a;i>a-b;i--)
            sum*=i;
        for(ll i=1;i<=b;i++)
            sum/=i;
        for(ll i=a;i>a-b;i--)
            sum*=i;
        printf("%lld
",sum);
    }
    return 0;
}