题目描述
Description

Input

Output
若无解,则输出”Impossible”。
否则第一行输出”Possible”,第二行输出 n 个正整数,依次输出序列 a 中每个数。
Sample Input
5 2 2
2 7
5 3
1 4 2 2 3
4 5 1 4
Sample Output
Possible
6 7 1000000000 6 3
Data Constraint
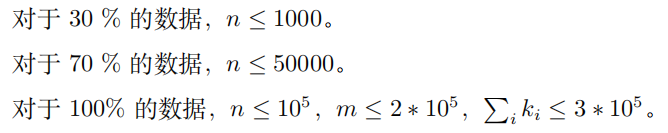
题解
线段树优化连边
ki向xij连边,xi与xi+1间的点向ki连边(线段树),线段树的点从下往上连边
一条从u到v的权值为s的边的意义是f[u]+s<=f[v],拓扑求max即可
初值就是给出的p和d(不需要求出相对大小然后再搞)
code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (a<b?a:b)
#define max(a,b) (a>b?a:b)
using namespace std;
struct type{
int s,x;
} b[100001];
int a[5000001][3];
int D[1000001];
int ls[1000001];
int d[1000001];
int f[1000001];
int F[1000001];
int c[100002];
int N,n,s,m,i,j,k,l,len,L,R,tot,h,t,mx;
void New(int x,int y,int z)
{
++len;
a[len][0]=y;
a[len][1]=ls[x];
ls[x]=len;
a[len][2]=z;
++D[y];
}
void mt(int t,int l,int r)
{
int mid=(l+r)/2;
N=max(N,t+n);
if (l==r) return;
mt(t*2,l,mid);
if (l<mid)
New(t*2+n,t+n,0);
else
New(l,t+n,0);
mt(t*2+1,mid+1,r);
if (mid+1<r)
New(t*2+1+n,t+n,0);
else
New(r,t+n,0);
}
void work(int t,int l,int r,int x,int y)
{
int mid=(l+r)/2;
if (x<=l && r<=y)
{
if (l==r)
New(l,N,1);
else
New(t+n,N,1);
return;
}
if (x<=mid)
work(t*2,l,mid,x,y);
if (mid<y)
work(t*2+1,mid+1,r,x,y);
}
int main()
{
freopen("web.in","r",stdin);
freopen("web.out","w",stdout);
scanf("%d%d%d",&n,&s,&m);
fo(i,1,n) f[i]=1;
fo(i,1,s)
scanf("%d%d",&b[i].x,&b[i].s),f[b[i].x]=b[i].s,F[b[i].x]=b[i].s;
mt(1,1,n);
fo(i,1,m)
{
++N;
scanf("%d%d%d",&L,&R,&tot);
fo(j,1,tot)
{
scanf("%d",&c[j]);
New(N,c[j],0);
}
c[0]=L-1;
c[++tot]=R+1;
fo(j,1,tot)
if (c[j-1]+1<=c[j]-1)
work(1,1,n,c[j-1]+1,c[j]-1);
}
h=0;t=0;
fo(i,1,N)
if (!D[i])
d[++t]=i;
while (h<t)
{
for (i=ls[d[++h]]; i; i=a[i][1])
{
f[a[i][0]]=max(f[a[i][0]],f[d[h]]+a[i][2]);
if (F[a[i][0]] && f[a[i][0]]>F[a[i][0]])
{
printf("Impossible
");
return 0;
}
--D[a[i][0]];
if (!D[a[i][0]])
d[++t]=a[i][0];
}
}
if (t<N)
{
printf("Impossible
");
return 0;
}
else
{
printf("Possible
");
fo(i,1,n)
printf("%d ",f[i]);
printf("
");
}
fclose(stdin);
fclose(stdout);
return 0;
}