uoj#513. 【UR #19】清扫银河

题目描述

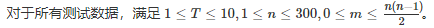
题解

很签到题

操作2先假设全部为黑，那么变成了每选一个点便会取反相连的边

如果能暴力搞出所有环就可以高斯消元判断，也许能过40

对原图建dfs树，发现只需要保留返祖边加上对应路径的环即可，任何的环都可以通过这些环异或得到，于是环的个数变为m级别，高斯消元O(m^3)可以70

设返祖边(u,v,w)的选择情况0/1为s，那么有w=u xor v xor s，移一下变成s=u xor v xor w

uv是未知数，w是常量，把s代到边里即可把规模变为n，前缀和+bitset解决

时间复杂度(O(n^3/omega))

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define ll long long
//#define file
using namespace std;

int a[90001][3],ls[301],d[301],c[301],T,n,m,i,j,k,l,len;
bitset<301> b[301],f[301],B;
bool bz[301];

void New(int x,int y,int z) {++len;a[len][0]=y;a[len][1]=ls[x];ls[x]=len;a[len][2]=z;}

void dfs(int Fa,int t)
{
	int i;
	bz[t]=1,d[t]=d[Fa]+1;
	
	for (i=ls[t]; i; i=a[i][1])
	if (!bz[a[i][0]])
	dfs(t,a[i][0]);
	else
	if (d[a[i][0]]<d[t]-1)
	{
		B[0]=a[i][2],B[t]=1,B[a[i][0]]=1;
		b[t]^=B,b[a[i][0]]^=B;
		B[0]=0,B[t]=0,B[a[i][0]]=0;
	}
}
void Dfs(int t)
{
	int i;
	bz[t]=0;
	
	for (i=ls[t]; i; i=a[i][1])
	if (bz[a[i][0]])
	{
		Dfs(a[i][0]),b[t]^=b[a[i][0]];
		f[a[i][0]]=b[a[i][0]],f[a[i][0]][0]=f[a[i][0]][0]^a[i][2],f[a[i][0]][t]=!f[a[i][0]][t],f[a[i][0]][a[i][0]]=!f[a[i][0]][a[i][0]];
	}
}

void work()
{
	memset(c,0,sizeof(c));
	fo(i,1,n)
	{
		fo(j,1,n)
		if (f[i][j])
		{
			if (!c[j]) {c[j]=i;break;}
			f[i]^=f[c[j]];
		}
		if (j>n && f[i][0]) {printf("no
");return;}
	}
	printf("yes
");
}

int main()
{
	#ifdef file
	freopen("uoj513.in","r",stdin);
	#endif
	
	scanf("%d",&T);
	for (;T;--T)
	{
		memset(ls,0,sizeof(ls)),len=0;
		scanf("%d%d",&n,&m);
		
		fo(i,1,m) scanf("%d%d%d",&j,&k,&l),New(j,k,l),New(k,j,l);
		fo(i,1,n) b[i]=f[i]=0;
		fo(i,1,n) if (!bz[i]) dfs(0,i);
		fo(i,1,n) if (bz[i]) Dfs(i);
		work();
	}
	
	fclose(stdin);
	fclose(stdout);
	return 0;
}