在知乎上看到一段介绍卷积神经网络的文章,感觉讲的特别直观明了,我整理了一下。首先介绍原理部分。
[透析] 卷积神经网络CNN究竟是怎样一步一步工作的?
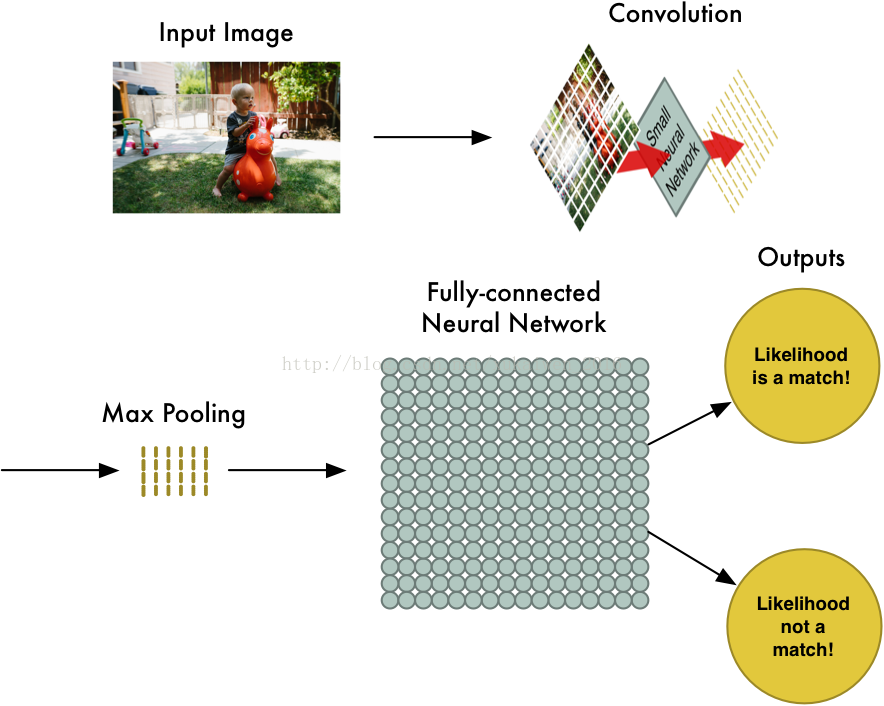
通过一个图像分类问题介绍卷积神经网络是如何工作的。下面是卷积神经网络判断一个图片是否包含“儿童”的过程,包括四个步骤:图像输入(InputImage)→卷积(Convolution)→最大池化(MaxPooling)→全连接神经网络(Fully-ConnectedNeural Network)计算。
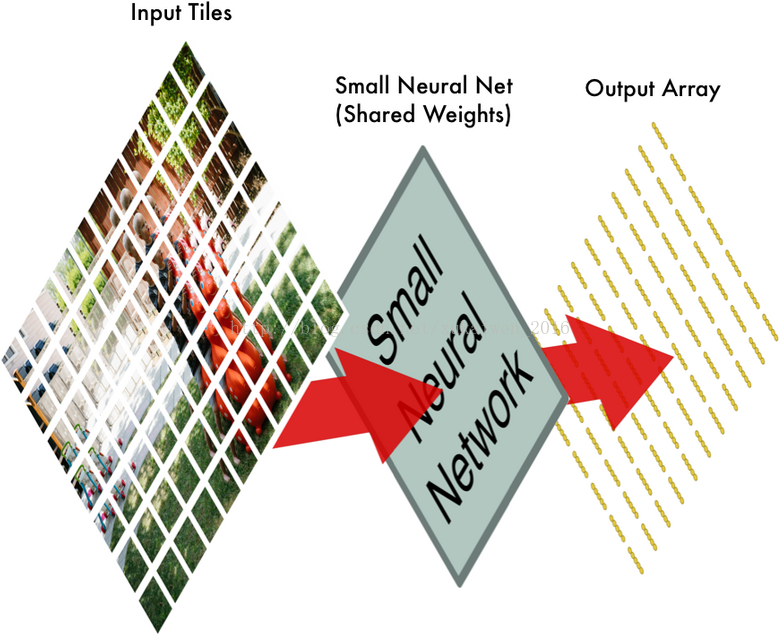
首先将图片分割成如下图的重叠的独立小块;下图中,这张照片被分割成了77张大小相同的小图片。
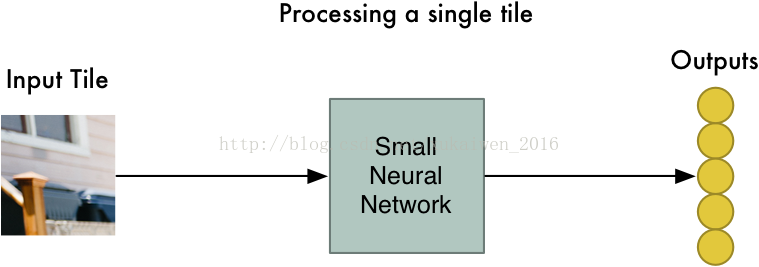
接下来将每一个独立小块输入小的神经网络;这个小的神经网络已经被训练用来判断一个图片是否属于“儿童”类别,它输出的是一个特征数组。
标准的数码相机有红、绿、蓝三个通道(Channels),每一种颜色的像素值在0-255之间,构成三个堆叠的二维矩阵;灰度图像则只有一个通道,可以用一个二维矩阵来表示。
将所有的独立小块输入小的神经网络后,再将每一个输出的特征数组按照第一步时77个独立小块的相对位置做排布,得到一个新数组。
第二步中,这个小的神经网络对这77张大小相同的小图片都进行同样的计算,也称权重共享(SharedWeights)。这样做是因为,第一,对图像等数组数据来说,局部数组的值经常是高度相关的,可以形成容易被探测到的独特的局部特征;第二,图像和其它信号的局部统计特征与其位置是不太相关的,如果特征图能在图片的一个部分出现,也能出现在任何地方。所以不同位置的单元共享同样的权重,并在数组的不同部分探测相同的模式。数学上,这种由一个特征图执行的过滤操作是一个离散的卷积,卷积神经网络由此得名。
卷积步骤完成后,再使用MaxPooling算法来缩减像素采样数组,按照2×2来分割特征矩阵,分出的每一个网格中只保留最大值数组,丢弃其它数组,得到最大池化数组(Max-PooledArray)。
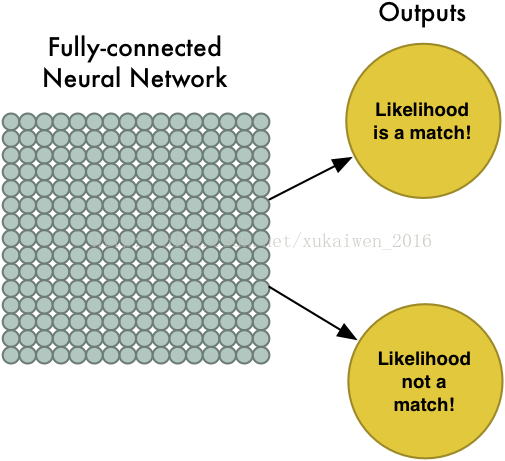
接下来将最大池化数组作为另一个神经网络的输入,这个全连接神经网络会最终计算出此图是否符合预期的判断。
在实际应用时,卷积、最大池化和全连接神经网络计算,这几步中的每一步都可以多次重复进行,总思路是将大图片不断压缩,直到输出单一的值。使用更多卷积步骤,神经网络就可以处理和学习更多的特征。
下面时代码,添加了详细注释:
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)# 读取图片数据集
sess = tf.InteractiveSession()# 创建session
# 一,函数声明部分
def weight_variable(shape):
# 正态分布,标准差为0.1,默认最大为1,最小为-1,均值为0
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
# 创建一个结构为shape矩阵也可以说是数组shape声明其行列,初始化所有值为0.1
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
# 卷积遍历各方向步数为1,SAME:边缘外自动补0,遍历相乘
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
# 池化卷积结果(conv2d)池化层采用kernel大小为2*2,步数也为2,周围补0,取最大值。数据量缩小了4倍
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],strides=[1, 2, 2, 1], padding='SAME')
# 二,定义输入输出结构
# 声明一个占位符,None表示输入图片的数量不定,28*28图片分辨率
xs = tf.placeholder(tf.float32, [None, 28*28])
# 类别是0-9总共10个类别,对应输出分类结果
ys = tf.placeholder(tf.float32, [None, 10])
keep_prob = tf.placeholder(tf.float32)
# x_image又把xs reshape成了28*28*1的形状,因为是灰色图片,所以通道是1.作为训练时的input,-1代表图片数量不定
x_image = tf.reshape(xs, [-1, 28, 28, 1])
# 三,搭建网络,定义算法公式,也就是forward时的计算
## 第一层卷积操作 ##
# 第一二参数值得卷积核尺寸大小,即patch,第三个参数是图像通道数,第四个参数是卷积核的数目,代表会出现多少个卷积特征图像;
W_conv1 = weight_variable([5, 5, 1, 32])
# 对于每一个卷积核都有一个对应的偏置量。
b_conv1 = bias_variable([32])
# 图片乘以卷积核,并加上偏执量,卷积结果28x28x32
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
# 池化结果14x14x32 卷积结果乘以池化卷积核
h_pool1 = max_pool_2x2(h_conv1)
## 第二层卷积操作 ##
# 32通道卷积,卷积出64个特征
w_conv2 = weight_variable([5,5,32,64])
# 64个偏执数据
b_conv2 = bias_variable([64])
# 注意h_pool1是上一层的池化结果,#卷积结果14x14x64
h_conv2 = tf.nn.relu(conv2d(h_pool1,w_conv2)+b_conv2)
# 池化结果7x7x64
h_pool2 = max_pool_2x2(h_conv2)
# 原图像尺寸28*28,第一轮图像缩小为14*14,共有32张,第二轮后图像缩小为7*7,共有64张
## 第三层全连接操作 ##
# 二维张量,第一个参数7*7*64的patch,也可以认为是只有一行7*7*64个数据的卷积,第二个参数代表卷积个数共1024个
W_fc1 = weight_variable([7*7*64, 1024])
# 1024个偏执数据
b_fc1 = bias_variable([1024])
# 将第二层卷积池化结果reshape成只有一行7*7*64个数据# [n_samples, 7, 7, 64] ->> [n_samples, 7*7*64]
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
# 卷积操作,结果是1*1*1024,单行乘以单列等于1*1矩阵,matmul实现最基本的矩阵相乘,不同于tf.nn.conv2d的遍历相乘,自动认为是前行向量后列向量
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# dropout操作,减少过拟合,其实就是降低上一层某些输入的权重scale,甚至置为0,升高某些输入的权值,甚至置为2,防止评测曲线出现震荡,个人觉得样本较少时很必要
# 使用占位符,由dropout自动确定scale,也可以自定义,比如0.5,根据tensorflow文档可知,程序中真实使用的值为1/0.5=2,也就是某些输入乘以2,同时某些输入乘以0
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(f_fc1,keep_prob) #对卷积结果执行dropout操作
## 第四层输出操作 ##
# 二维张量,1*1024矩阵卷积,共10个卷积,对应我们开始的ys长度为10
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
# 最后的分类,结果为1*1*10 softmax和sigmoid都是基于logistic分类算法,一个是多分类一个是二分类
y_conv=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)
# 四,定义loss(最小误差概率),选定优化优化loss,
cross_entropy = -tf.reduce_sum(ys * tf.log(y_conv)) # 定义交叉熵为loss函数
train_step = tf.train.DradientDescentOptimizer(0.5).minimize(cross_entropy) # 调用优化器优化,其实就是通过喂数据争取cross_entropy最小化
# 五,开始数据训练以及评测
correct_prediction = tf.equal(tf.argmax(y_conv,1), tf.argmax(ys,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
tf.global_variables_initializer().run()
for i in range(20000):
batch = mnist.train.next_batch(50)
if i%100 == 0:
train_accuracy = accuracy.eval(feed_dict={x:batch[0], ys: batch[1], keep_prob: 1.0})
print("step %d, training accuracy %g"%(i, train_accuracy))
train_step.run(feed_dict={x: batch[0], ys: batch[1], keep_prob: 0.5})
print("test accuracy %g"%accuracy.eval(feed_dict={x: mnist.test.images, ys: mnist.test.labels, keep_prob: 1.0}))