CTR学习笔记系列的第一篇,总结在深度模型称王之前经典LR,FM, FFM模型,这些经典模型后续也作为组件用于各个深度模型。模型分别用自定义Keras Layer和estimator来实现,哈哈一个是旧爱一个是新欢。特征工程依赖feature_column实现,这里做的比较简单在后面的深度模型再好好搞。
问题定义
CTR本质是一个二分类问题,$X in R^N $是用户和广告相关特征, (Y in (0,1))是每个广告是否被点击,基础模型就是一个简单的Logistics Regression
考虑在之后TF框架里logistics可以简单用activation来表示,我们把核心的部分简化为以下

## LR模型 2010年之前主流的CTR模型通常是最简单的logistics regression,模型可解释性强,工程上部署简单快捷。但最大的问题是依赖于大量的手工特征工程。
刚接触特征工程的同学可能会好奇为什么需要计算组合特征?
最开始我只是简单认为越细粒度的聚合特征Bias越小。接触了因果推理后,我觉得更适合用Simpson Paradox里的Confounder Bias来解释,不同聚合特征之间可能会相悖,例如各个年龄段的男性点击率均低于女性,但整体上男性的点击率高于女性。感兴趣的可以看看这篇博客因果推理的春天系列序 - 数据挖掘中的Confounding, Collidar, Mediation Bias
如果即想简化特征工程,又想加入特征组合,肯定就会想到下面的暴力特征组合方式。这个也被称作POLY2模型
但上述(w_{i,j})需要学习(frac{n(n-1)}{2})个参数,一方面复杂度高,另一方面对高维稀疏特征会出现大量(w_{i,j})是0的情况,模型无法学到样本中未曾出现的特征组合pattern,模型泛化性差。
于是降低复杂度,自动选择有效特征组合,以及模型泛化这三点成为后续主要的改进的方向。
GBDT+LR模型
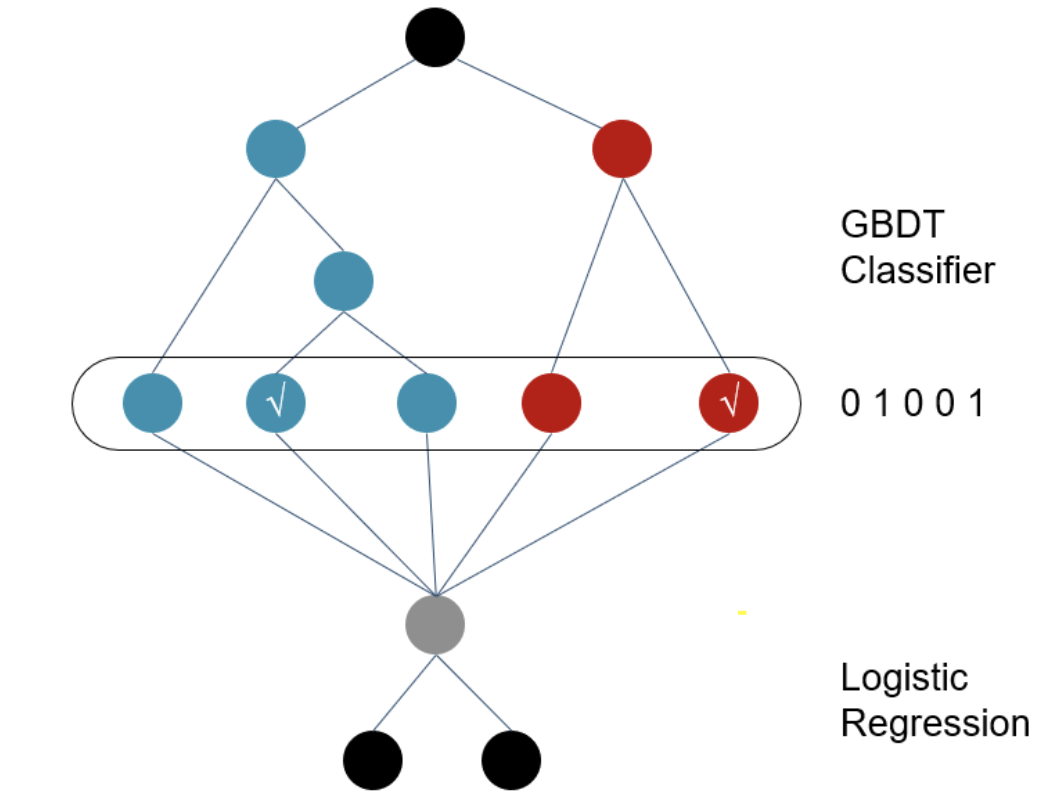
2014年Facebook提出在GBDT叠加LR的方法,敲开了特征工程模型化的大门。GBDT输出的不是预测概率,而是每一个样本落在每一颗子树哪个叶节点的一个0/1矩阵。在只保留和target相关的有效特征组合的同时,避免了手工特征组合需要的业务理解和人工成本。
相较特征组合,我更喜欢把GBDT输出的特征向量,理解为根据target,对样本进行了聚类/降维,输出的是该样本所属的几个特定人群组合,每一棵子树都对应一种类型的人群组合。
但是!GBDT依旧存在泛化问题,因为所有叶节点的选择都依赖于训练样本,并且GBDT在离散特征上效果比较有限。同时也存在经过GBDT变换得到的特征依旧是高维稀疏特征的问题。
FM模型
2010年Rendall提出的因子分解机模型(FM)为降低计算复杂度,为增加模型泛化能力提供了思路
原理
FM模型将上述暴力特征组合直接求解整个权重矩(w_ij in R^{N*N}),转化为求解权重矩阵的隐向量(V in R^{N*k}),这一步会大大增加模型泛化能力,因为权重矩阵不再完全依赖于样本中的特定特征组合,而是可以通过特征间的相关关系间接得到。 同时隐向量把模型需要学习的参数数量从(frac{n(n-1)}{2})降低到(nk)个
同时FM通过下面的trick,把拟合过程的计算复杂度从(O(n^2k))降低到线性复杂度(O(nk))
代码实现-自定义Keras Layer
class FM_Layer(Layer):
"""
Input:
factor_dim: latent vector size
input_shape: raw feature size
activation
output:
FM layer output
"""
def __init__(self, factor_dim, activation = None, **kwargs):
self.factor_dim = factor_dim
self.activation = activations.get(activation) # if None return linear, else return function of identifier
self.InputSepc = InputSpec(ndim=2) # Specifies input layer attribute. one Inspec for each input
super(FM_Layer,self).__init__(**kwargs)
def build(self, input_shape):
"""
input:
tuple of input_shape
output:
w: linear weight
v: latent vector
b: linear Bias
func:
define all the necessary variable here
"""
assert len(input_shape) >=2
input_dim = int(input_shape[-1])
self.w = self.add_weight(name = 'w0', shape = (input_dim, 1),
initializer = 'glorot_uniform',
trainable = True)
self.b = self.add_weight(name = 'bias', shape = (1, ),
initializer = 'zeros',
trainable = True)
self.v = self.add_weight(name = 'hidden_vector', shape = (input_dim, self.factor_dim),
initializer = 'glorot_uniform',
trainable = True)
super(FM_Layer, self).build(input_shape)# set self.built=True
def call(self, x):
"""
input:
x(previous layer output)
output:
core calculation of the FM layer
func:
core calculcation of layer goes here
"""
linear_term = K.dot(x, self.w) + self.b
# Embedding之和,Embedding内积: (1, input_dim) * (input_dim, factor_dim) = (1, factor_dim)
sum_square = K.pow(K.dot(x, self.v),2)
square_sum = K.dot(K.pow(x, 2), K.pow(self.v, 2))
# (1, factor_dim) -> (1)
quad_term = K.mean( (sum_square - square_sum), axis=1, keepdims = True) #
output = self.activation((linear_term+quad_term))
return output
def compute_output_shape(self, input_shape):
# tf.keras回传input_shape是tf.dimension而不是tuple, 所以要cast成int
return (int(input_shape[0]), self.output_dim)
FM和MF的关系
Factorizaton Machine 和Matrix Factorization听起来就很像,MF也确实是FM的一个特例。MF是通过对矩阵进行因子分解得到隐向量,但因为只适用于矩阵所以特征只能是二维,常见的是(user_id, item_id)组合。而同样是得到隐向量,FM将矩阵展平把离散特征都做one-hot,因此支持任意数量的输入特征。

FM和Embedding的关系
Embedding最常见于NLP中,把词的高维稀疏特征映射到低维矩阵embedding中,然后用交互函数,例如向量内积来表示词与词之间的相似度。而实际上FM计算的隐向量也是一种Embedding 的拟合方法,并且限制了只用向量内积作为交互函数。上述(X*V in R^{K})得到的就是Embedding向量本身。
FFM
2015年提出的FFM模型在FM的基础上加入了Field的概念
原理
上述FM学到的权重矩阵V是每个特征对应一个隐向量,两特征组合通过隐向量内积的形式来表达。FFM提出同一个特征和不同Field的特征组合应该有不同的隐向量,因此(V in R^{N*K})变成 (V in R^{N*F*K})其中F是特征所属Field的个数。以下数据中country,Data,Ad_type就是Field((F=3))

FM两特征交互的部分被改写为以下,因此需要学习的参数数量从nk变为nf*k。并且在拟合过程中无法使用上述trick因此复杂度从FM的(O(nk))上升为(O(kn^2))。
代码实现-自定义model_fn
def model_fn(features, labels, mode, params):
"""
Field_aware factorization machine for 2 classes classification
"""
feature_columns, field_dict = build_features()
field_dim = len(np.unique(list(field_dict.values())))
input = tf.feature_column.input_layer(features, feature_columns)
input_dim = input.get_shape().as_list()[-1]
with tf.variable_scope('linear'):
init = tf.random_normal( shape = (input_dim,2) )
w = tf.get_variable('w', dtype = tf.float32, initializer = init, validate_shape = False)
b = tf.get_variable('b', shape = [2], dtype= tf.float32)
linear_term = tf.add(tf.matmul(input,w), b)
tf.summary.histogram( 'linear_term', linear_term )
with tf.variable_scope('field_aware_interaction'):
init = tf.truncated_normal(shape = (input_dim, field_dim, params['factor_dim']))
v = tf.get_variable('v', dtype = tf.float32, initializer = init, validate_shape = False)
interaction_term = tf.constant(0, dtype =tf.float32)
# iterate over all the combination of features
for i in range(input_dim):
for j in range(i+1, input_dim):
interaction_term += tf.multiply(
tf.reduce_mean(tf.multiply(v[i, field_dict[j],: ], v[j, field_dict[i],:])) ,
tf.multiply(input[:,i], input[:,j])
)
interaction_term = tf.reshape(interaction_term, [-1,1])
tf.summary.histogram('interaction_term', interaction_term)
with tf.variable_scope('output'):
y = tf.math.add(interaction_term, linear_term)
tf.summary.histogram( 'output', y )
if mode == tf.estimator.ModeKeys.PREDICT:
predictions = {
'predict_class': tf.argmax(tf.nn.softmax(y), axis=1),
'prediction_prob': tf.nn.softmax(y)
}
return tf.estimator.EstimatorSpec(mode = tf.estimator.ModeKeys.PREDICT,
predictions = predictions)
cross_entropy = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits( labels=labels, logits=y ))
if mode == tf.estimator.ModeKeys.TRAIN:
optimizer = tf.train.AdamOptimizer(learning_rate = params['learning_rate'])
train_op = optimizer.minimize(cross_entropy,
global_step = tf.train.get_global_step())
return tf.estimator.EstimatorSpec(mode, loss = cross_entropy, train_op = train_op)
else:
eval_metric_ops = {
'accuracy': tf.metrics.accuracy(labels = labels,
predictions = tf.argmax(tf.nn.softmax(y), axis=1)),
'auc': tf.metrics.auc(labels = labels ,
predictions = tf.nn.softmax(y)[:,1]),
'pr': tf.metrics.auc(labels = labels,
predictions = tf.nn.softmax(y)[:,1],
curve = 'PR')
}
return tf.estimator.EstimatorSpec(mode, loss = cross_entropy, eval_metric_ops = eval_metric_ops)
完整代码在这里 https://github.com/DSXiangLi/CTR
参考资料
- S. Rendle, “Factorization machines,” in Proceedings of IEEE International Conference on Data Mining (ICDM), pp. 995–1000, 2010
- Yuchin Juan,Yong Zhuang,Wei-Sheng Chin,Field-aware Factorization Machines for CTR Prediction。
- 盘点前深度学习时代阿里、谷歌、Facebook的CTR预估模型
- 前深度学习时代CTR预估模型的演化之路:从LR到FFM
- 推荐系统召回四模型之:全能的FM模型
- 主流CTR预估模型的演化及对比
- 深入FFM原理与实践